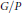Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T09:07:48.468Z Has data issue: false hasContentIssue false
  • English
  • Français

A Coincidence Theorem for Holomorphic Maps to $G/P$

Published online by Cambridge University Press:  20 November 2018

Parameswaran Sankaran
Parameswaran Sankaran*
Affiliation:
Institute of Mathematical Sciences, CIT Campus, Chennai 600 113, India, email: sankaran@imsc.ernet.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to extend to an arbitrary generalized Hopf and Calabi-Eckmann manifold the following result of Kalyan Mukherjea: Let 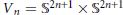${{V}_{n}}={{\mathbb{S}}^{2n+1}}\times {{\mathbb{S}}^{2n+1}}$ denote a Calabi-Eckmann manifold. If 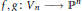$f,g:\,{{V}_{n}}\to {{\mathbb{P}}^{n}}$ are any two holomorphic maps, at least one of them being non-constant, then there exists a coincidence: 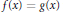$f(x)\,=\,g(x)$ for some 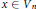$x\in {{V}_{n}}$. Our proof involves a coincidence theorem for holomorphic maps to complex projective varieties of the form 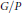$G/P$ where 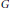$G$ is complex simple algebraic group and 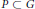$P\,\subset \,G$ is a maximal parabolic subgroup, where one of the maps is dominant.

Keywords

32H0254M20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 291 - 298
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Calabi, E. and Eckmann, B., A class of compact complex manifolds which are not algebraic. Ann.Math. 58 (1953), 494–500.Google Scholar
[2] Glover, H. and Homer, W., Fixed points on flag manifolds. Pacific J. Math. 101 (1982), 303–306.Google Scholar
[3] Glover, H. and Homer, W., Endomorphisms of the cohomology ring of finite Grassmann manifolds. Springer Lecture Notes in Math. 657 (1978), 170–193.Google Scholar
[4] Grauert, H. and Remmert, R., Über kompakte homogene komplexe Mannifaltigkeiten. Arch. Math. 13 (1962), 498–507.Google Scholar
[5] Hironaka, H., Bimeromorphic smoothings of a complex analytic space. Acta Math. Vietnam 2 (1977), 103–168.Google Scholar
[6] Hirzebruch, F., Topological methods in algebraic geometry. GrundlehrenMath.Wiss. 131, Springer-Verlag, Berlin, 1978.Google Scholar
[7] Kantor, I. L., The cross ratio of points and invariants on homogeneous spaces with parabolic stationary groups-I. (Russian) Trud. Sem. Vekt. Tenz. Anal. 17 (1974), 250–313.Google Scholar
[8] Kleiman, S., The transversality of a general translate. Compositio Math. 28 (1974), 287–297.Google Scholar
[9] Kumar, S. and Nori, M., Positivity of the cup product in cohomology of flag varieties associated to Kac-Moody groups. Internat.Math. Res. Notices 14 (1998), 757–763.Google Scholar
[10] Lescure, F., Example d'actions induites non résolubles sur la cohomologie de Dolbeault. Topology 35 (1995), 561–581.Google Scholar
[11] Milnor, J. and Stasheff, J., Characteristic classes. Ann.Math. Stud. 76, Princeton University Press, Princeton, 1974.Google Scholar
[12] Mukherjea, Kalyan, Coincidence theory.topological and holomorphic. In: Topology Hawaii (Honolulu, HI, 1990),World Sci. Publ., River Edge, NJ, 1992, 191–199.Google Scholar
[13] Paranjape, K. H. and Srinivas, V., Self maps of homogeneous spaces. Invent.Math. 98 (1998), 425–444.Google Scholar
[14] Ramani, V. and Sankaran, P., Dolbeault cohomology of compact complex homogeneous spaces. Proc. Ind. Acad. Sci. (Math. Sci.) 109 (1999), 11–21.Google Scholar
[15] Serre, J.-P., Géométrie algébrique et géométrie analytique. Ann. Inst. Fourier (Grenoble) 6(1955–1956), 1–42.Google Scholar
[16] Spanier, E. H., Algebraic Topology. Springer-Verlag, New York, 1966.Google Scholar
[17] Toledo, D., On the Atiyah-Bott formula for isolated fixed points. J. Differential Geom. 8 (1973), 401–436.Google Scholar
[18] Wang, H. C., Closed manifolds with homogeneous complex structures. Amer. J. Math. 76 (1954), 1–32.Google Scholar