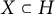1 Introduction and statements of the results
In the sequel, H is a real Hilbert space, with
$\mathrm {dim}(H)\geq 2$
,
$\Omega $
is an open convex subset of H and
$\Phi :\Omega \to H$
is a given operator.
We say that
$\Phi $
has a Lipschitzian derivative if
$\Phi $
is Fréchet differentiable and the derivative of
$\Phi $
, denoted by
$\Phi '$
, is Lipschitzian, i.e., one has
$$ \begin{align*}\sup_{x,y\in \Omega, x\neq y}{{\|\Phi'(x)-\Phi'(y)\|_{\mathcal{L}(H)}}\over {\|x-y\|}}<+\infty,\end{align*} $$
where
$\mathcal {L}(H)$
is the space of all continuous linear operators from H into itself endowed with the norm
$$ \begin{align*}\|T\|_{\mathcal{L}(H)}=\sup_{\|x\|\leq 1}\|T(x)\|.\end{align*} $$
For a generic set
$A\subseteq H$
, we denote by
$\overline {\mathrm {conv}}(A)$
the closed convex hull of A, i.e., the smallest closed convex set containing A.
We are interested in the existence of zeros for
$\Phi $
.
To shorten the statements, we now introduce the following notations. Namely, for each convex set
$X\subseteq H$
, we set
$$ \begin{align*}\delta_X:=\inf_{\psi\in \Gamma_X}\left(\sup_{x\in X}(\|x\|^2+\psi(x))-\inf_{x\in X}(\|x\|^2+\psi(x))\right),\end{align*} $$
where
$\Gamma _X$
denotes the family of all convex functions
$\psi :X\to \mathbf {R}$
.
We have
Proposition 1.1 Let
$X\subseteq H$
be a convex set with more than one point. Then,
$\delta _X>0$
.
We will get Proposition 1.1 as a by-product of Theorem 1.1 below. In [Reference Zalinescu2], C. Zalinescu provided a proof of Proposition 1.1 based on quite hard arguments of convex analysis.
Moreover, for each subset V of
$\Omega $
, we denote by
$\mathcal {A}_V$
the family of all convex sets
$X\subseteq V$
such that
$$ \begin{align*}0\in \overline{\mathrm{conv}}(\Phi(X)).\end{align*} $$
The aim of this very short note is to establish the following result
Theorem 1.1 Assume that
$\Phi $
is a
$C^1$
operator with Lipschitzian derivative and let V be a subset of
$\Omega $
such that
$\Phi (V)$
is closed. Then, the following assertions are equivalent:
(1)
$0\in \Phi (V)$
;
(2)
$\inf _{X\in \mathcal {A}_{V}}\delta _X=0$
.
More precisely, the key result of this note is Theorem 1.2 below. Theorem 1.1 then follows as a by-product of it.
Theorem 1.2 Assume that
$\Phi $
is a
$C^1$
operator such that
$\Phi '$
is Lipschitzian, with Lipschitz constant L. Let V be a subset of
$\Omega $
such that
$$ \begin{align*}\eta:=\inf_{x\in V}\|\Phi(x)\|>0.\end{align*} $$
Then, for each convex set
$X\subset V$
such that
$\delta _X<{{2\eta }\over {L}}$
, one has
$$ \begin{align*}0\not\in\overline{\mathrm{conv}}(\Phi(X)).\end{align*} $$
We will prove Theorem 1.2 and Theorem 1.1 as well in the next section. The main tool that we will use is the classical Kneser minimax theorem [Reference Kneser1]. For the reader convenience, we recall its statement
Theorem 1.A Let E be a vector space, F a locally convex topological vector space,
$X\subseteq E$
a convex set and
$Y\subset F$
a compact convex set. Moreover, let
$h:X\times Y\to \mathbf {R}$
be a function which is convex in X and upper semicontinuous and concave in Y. Then, one has
$$ \begin{align*}\sup_Y\inf_Xh=\inf_X\sup_Yh.\end{align*} $$
The interest of Theorem 1.1 resides mainly in its full novelty which is, in turn, due to the particular proof approach based on Theorem 1.A. Actually, we are not aware of known results with which Theorem 1.1 can be compared even in a vague manner.
In particular, it seems that the number
$\delta _X$
is here introduced for the first time. We think that it is worth studying in depth. For instance, it would be useful to provide an explicit positive lower bound for it. Indeed, the current proofs of Proposition 1.1 (ours and that in [Reference Zalinescu2]) are highly indirect.
Another interesting feature of Theorem 1.1 resides in the derivative of
$\Phi $
: not only it does not appear in the conclusion at all, but also it needs to be Lipschitzian. In this connection, the following example is enlightening.
Example 1.1 Let
$h:\mathbf {R}\to \mathbf {R}$
be any
$C^1$
function with the following property:
$[-\pi ,\pi ]\subseteq h(\mathbf {R})$
and there exist two sequences in
$(0,+\infty )$
$\{\alpha _n\}, \{\beta _n\}$
such that
$$ \begin{align*}\lim_{n\to \infty}\alpha_n=+\infty,\end{align*} $$
$$ \begin{align*}\lim_{n\to \infty}(\beta_n^2-\alpha_n^2)=0,\end{align*} $$
$$ \begin{align*}\alpha_n<\beta_n,\end{align*} $$
$$ \begin{align*}h(\alpha_n)=0,\end{align*} $$
$$ \begin{align*}h(\beta_n)=-\pi,\end{align*} $$
for all
$n\in \mathbf {N}$
. For instance, one can take:
$h(x)=\pi \sin (2\pi x^2)$
,
$\alpha _n=\sqrt {n}$
,
$\beta _n=\sqrt {n+{{3}\over {4}}}$
. Then, consider the function
$\Phi :\mathbf {R}^2\to \mathbf {R}^2$
defined by
$$ \begin{align*}\Phi(x,y)=(\sin(h(x)), \cos(h(x))),\end{align*} $$
for all
$(x,y)\in \mathbf {R}^2$
. So,
$\Phi $
is
$C^1$
and
$$ \begin{align*}\Phi(\mathbf{R}^2)=\{(s,t)\in \mathbf{R}^2 : s^2+t^2=1\}.\end{align*} $$
In connection with Theorem 1.1, take
$\Omega =V=\mathbf {R}^2$
. Now, fix
$\epsilon>0$
and
$n\in \mathbf {N}$
so that
$\beta _n^2-\alpha _n^2<\epsilon $
. Set
$$ \begin{align*}X:=[\alpha_n,\beta_n]\times \{0\}.\end{align*} $$
So, X is convex and the points
$(0,1)$
,
$(0,-1)$
belong to
$\Phi (X)$
. Consequently
$$ \begin{align*}0\in \mathrm{conv}(\Phi(X)).\end{align*} $$
Therefore,
$X\in \mathcal {A}_V$
. Moreover, we have
$$ \begin{align*}\delta_X\leq \sup_{(x,y)\in X}\|(x,y)\|^2-\inf_{(x,y)\in X}\|(x,y)\|^2=\beta_n^2-\alpha_n^2<\epsilon.\end{align*} $$
This shows that
$$ \begin{align*}\inf_{Y\in \mathcal{A}_V}\delta_Y=0.\end{align*} $$
However,
$\Phi (V)$
is closed and
$0\not \in \Phi (V)$
. So, the implication
$(2)\to (1)$
in Theorem 1.1 does not hold.
2 Proofs
Proof of Theorem 1.2
Fix any convex set
$X\subset V$
and any convex function
$\psi :X\to \mathbf {R}$
satisfying
$$ \begin{align} \sup_{x\in X}(\|x\|^2+\psi(x))-\inf_{x\in X}(\|x\|^2+\psi(x))<{{2\eta}\over {L}}. \end{align} $$
Of course, pairs
$(X,\psi )$
of this type do exist: for instance, this is the case when X is a singleton. Set
$$ \begin{align*}Y=\{x\in H : \|x\|\leq 1\},\end{align*} $$
and consider the functions
$\varphi :X\to \mathbf {R}$
,
$f:\Omega \times Y\to \mathbf {R}$
and
$g:X\times Y\to \mathbf {R}$
defined by
$$ \begin{align*}\varphi(x)={{L}\over {2}}(\|x\|^2+\psi(x)),\end{align*} $$
$$ \begin{align*}f(x,y)=\langle \Phi(x),y\rangle,\end{align*} $$
and
$$ \begin{align*}g(x,y)=f(x,y)+\varphi(x).\end{align*} $$
We claim that
$$ \begin{align} \inf_X\sup_Yf-\sup_Y\inf_Xf\leq \sup_X\varphi-\inf_X\varphi. \end{align} $$
Arguing by contradiction, assume that
$$ \begin{align*}\inf_X\sup_Yf-\sup_Y\inf_Xf> \sup_X\varphi-\inf_X\varphi.\end{align*} $$
We then would have
$$ \begin{align} \sup_Y\inf_Xg\leq \sup_Y\inf_Xf+\sup_X\varphi<\inf_X\sup_Yf+\inf_X\varphi\leq\inf_X\sup_Yg. \end{align} $$
For each
$y\in Y$
, the function
$f(\cdot ,y)$
is
$C^1$
and its derivative (denoted by
$f^{\prime }_x(\cdot ,y)$
) is given by
$$ \begin{align*}\langle f^{\prime}_x(x,y),u\rangle=\langle\Phi'(x)(u),y\rangle\end{align*} $$
for all
$x\in \Omega $
,
$u\in H$
. Also, for each
$v, w\in \Omega $
, we have
$$ \begin{align} \|f^{\prime}_x(v,y)-f^{\prime}_x(w,y)\|&=\sup_{u\in Y}|\langle\Phi'(v)(u)-\Phi'(w)(u),y\rangle|\leq \sup_{u\in Y}\|\Phi'(v)(u)-\Phi'(w)(u)\|\nonumber\\&=\|\Phi'(v)-\Phi'(w)\|_{\mathcal{L}(H)}\leq L\|v-w\|. \end{align} $$
Taking (2.4) into account, we also have
$$ \begin{align*}\langle Lv+f^{\prime}_x(v,y)-Lw-f^{\prime}_x(w,y),v-w\rangle\end{align*} $$
$$ \begin{align*}\geq L\|v-w\|^2-\|f^{\prime}_x(v,y)-f^{\prime}_x(w,y)\|\|v-w\|\geq L\|v-w\|^2-L\|v-w\|^2=0.\end{align*} $$
In other words, the derivative of the function
${{L}\over {2}}\|\cdot \|^2+f(\cdot ,y)$
is monotone in
$\Omega $
and so the function is convex there ([Reference Zeidler3], Proposition 42.6). This implies that
$g(\cdot ,y)$
is convex in X since
$\psi $
is so. Furthermore, Y is weakly compact and, for each
$x\in X$
, the function
$g(x,\cdot )$
is weakly continuous, being affine and continuous. Hence, applying Theorem 1.A, we would have
$$ \begin{align*}\sup_Y\inf_Xg=\inf_X\sup_Yg,\end{align*} $$
contradicting (2.3). So, (2.2) does hold. Notice that
$$ \begin{align*}\inf_X\sup_Yf=\inf_{x\in X}\|\Phi(x)\|.\end{align*} $$
Therefore, from (2.2) we infer that
$$ \begin{align*}{{L}\over {2}}\left(\inf_{x\in X}(\|x\|^2+\psi(x))-\sup_{x\in X}(\|x\|^2+\psi(x))\right)+\inf_{x\in X}\|\Phi(x)\|\leq \sup_{y\in Y}\inf_{x\in X}\langle \Phi(x),y\rangle,\end{align*} $$
and hence, in view of (2.1), taking into account that
$\eta \leq \inf _{x\in X}\|\Phi (x)\|$
, we have
$$ \begin{align*}0<\sup_{y\in Y}\inf_{x\in X}\langle \Phi(x),y\rangle.\end{align*} $$
Because of this inequality, we can fix
$\gamma>0$
and
$\tilde y\in Y$
so that
$$ \begin{align*}\inf_{x\in X}\langle\Phi(x),\tilde y\rangle\geq \gamma.\end{align*} $$
Thus, if we set
$$ \begin{align*}C=\{u\in H : \langle u,\tilde y\rangle\geq \gamma\},\end{align*} $$
we have
$$ \begin{align*}\overline{\mathrm{conv}}(\Phi(X))\subset C,\end{align*} $$
since C is closed and convex, while
$0\not \in C$
and the proof is complete.
Proof of Theorem 1.1
The implication
$(1)\to (2)$
is immediate. Indeed, if there exists
$\tilde x\in V$
such that
$\Phi (\tilde x)=0$
, then the singleton
$\{\tilde x\}$
belongs to the family
$\mathcal {A}_{V}$
and
$\delta _{\{\tilde x\}}=0$
, and so
$(2)$
holds. Viceversa, assume that
$(2)$
holds. We have to prove
$(1)$
. Arguing by contradiction, suppose that
$0\not \in \Phi (V)$
. Since
$\Phi (V)$
is closed, this implies that
$\inf _{x\in V}\|\Phi (x)\|>0$
. By assumption, there is a convex set
$X\subset V$
such that
$$ \begin{align*}\delta_X<2{{\inf_{x\in V}\|\Phi(x)\|}\over {L}}\end{align*} $$
and
$$ \begin{align*}0\in \overline {\mathrm{conv}}(\Phi(X)),\end{align*} $$
contradicting Theorem 1.2.
From the proof of Theorem 1.1, it clearly follows the following.
Theorem 2.1 Assume that
$\Phi $
is a
$C^1$
operator with Lipschitzian derivative and let V be a subset of
$\Omega $
such that
$$ \begin{align*}\inf_{X\in \mathcal{A}_{V}}\delta_X=0.\end{align*} $$
Then,
$\inf _{x\in V}\|\Phi (x)\|=0$
.
Proof of Proposition 1.1
Arguing by contradiction, assume that there is a convex set
$X\subset H$
, with more than one point, such that
$\delta _X=0$
. Fix
$x_1, x_2\in X$
, with
$x_1\neq x_2$
. Let V be the closed segment joining
$x_1$
with
$x_2$
. Clearly,
$\delta _V=0$
. Fix
$u, v, w\in H$
so that
$\langle u,v\rangle =0$
,
$\|u\|=\|v\|=1$
,
$\langle w,x_1\rangle \neq \langle w,x_2\rangle $
. Finally, consider the operator
$\Phi :H\to H$
defined by
$$ \begin{align*}\Phi(x)=\sin\left({{\langle w,x-x_1\rangle\pi}\over {\langle w,x_2-x_1\rangle}}\right)u+\cos\left({{\langle w,x-x_1\rangle\pi}\over {\langle w,x_2-x_1\rangle}}\right)v.\end{align*} $$
Of course,
$\Phi $
has a Lipschitzian derivative,
$\Phi (V)$
is compact and
$0\not \in \Phi (V)$
. Moreover,
$\Phi (x_1)=v$
and
$\Phi (x_2)=-v$
. Consequently,
$0\in \mathrm {conv}(\Phi (V))$
and so
$V\in \mathcal {A}_V$
. Hence, condition
$(2)$
of Theorem 1.1 is satisfied and not condition
$(1)$
. This contradiction ends the proof.
Acknowledgements
The author wishes to thank the referee for his/her remarks showing the excessive conciseness of the original version.
Funding
This work has been funded by the European Union - NextGenerationEU Mission 4 - Component 2 - Investment 1.1 under the Italian Ministry of University and Research (MUR) programme “PRIN 2022” - grant number 2022BCFHN2 - Advanced theoretical aspects in PDEs and their applications - CUP: E53D23005650006. The author has also been supported by the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM) and by the Università degli Studi di Catania, PIACERI 2020-2022, Linea di intervento 2, Progetto “MAFANE”.
