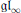 $\mathfrak{g}{{\mathfrak{l}}_{\infty }}$
$\mathfrak{g}{{\mathfrak{l}}_{\infty }}$Published online by Cambridge University Press: 20 November 2018
Let 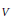 $V$ be a vector space over a field
$V$ be a vector space over a field 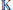 $\mathbb{K}$ of characteristic zero and
$\mathbb{K}$ of characteristic zero and 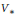 ${{V}_{*}}$ be a space of linear functionals on
${{V}_{*}}$ be a space of linear functionals on 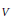 $V$ which separate the points of
$V$ which separate the points of 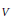 $V$. We consider
$V$. We consider 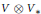 $V\,\otimes \,{{V}_{*}}$ as a Lie algebra of finite rank operators on
$V\,\otimes \,{{V}_{*}}$ as a Lie algebra of finite rank operators on 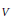 $V$, and set
$V$, and set 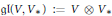 $\mathfrak{g}\mathfrak{l}(V,\,{{V}_{*}})\,:=\,V\,\otimes \,{{V}_{*}}$. We define a Cartan subalgebra of
$\mathfrak{g}\mathfrak{l}(V,\,{{V}_{*}})\,:=\,V\,\otimes \,{{V}_{*}}$. We define a Cartan subalgebra of 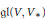 $\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ as the centralizer of a maximal subalgebra every element of which is semisimple, and then give the following description of all Cartan subalgebras of
$\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ as the centralizer of a maximal subalgebra every element of which is semisimple, and then give the following description of all Cartan subalgebras of 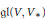 $\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ under the assumption that
$\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ under the assumption that 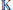 $\mathbb{K}$ is algebraically closed. A subalgebra of
$\mathbb{K}$ is algebraically closed. A subalgebra of 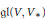 $\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ is a Cartan subalgebra if and only if it equals
$\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ is a Cartan subalgebra if and only if it equals 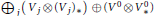 ${{\oplus }_{j}}({{V}_{j}}\,\otimes {{({{V}_{j}})}_{*}})\,\oplus \,({{V}^{0}}\,\otimes \,V_{*}^{0})$ for some one-dimensional subspaces
${{\oplus }_{j}}({{V}_{j}}\,\otimes {{({{V}_{j}})}_{*}})\,\oplus \,({{V}^{0}}\,\otimes \,V_{*}^{0})$ for some one-dimensional subspaces 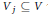 ${{V}_{j}}\subseteq V$ and
${{V}_{j}}\subseteq V$ and 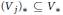 ${{\text{(}{{V}_{j}}\text{)}}_{*}}\subseteq {{V}_{*}}$ with
${{\text{(}{{V}_{j}}\text{)}}_{*}}\subseteq {{V}_{*}}$ with 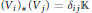 ${{({{V}_{i}})}_{*}}({{V}_{j}})\,=\,{{\delta }_{ij}}\mathbb{K}$ and such that the spaces
${{({{V}_{i}})}_{*}}({{V}_{j}})\,=\,{{\delta }_{ij}}\mathbb{K}$ and such that the spaces 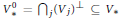 $V_{*}^{0}=\bigcap{_{j}}{{({{V}_{j}})}^{\bot }}\subseteq {{V}_{*}}$ and
$V_{*}^{0}=\bigcap{_{j}}{{({{V}_{j}})}^{\bot }}\subseteq {{V}_{*}}$ and  ${{V}^{0}}=\bigcap{_{j}}{{\left( {{({{V}_{j}})}_{*}} \right)}^{\bot }}\subseteq V$ satisfy
${{V}^{0}}=\bigcap{_{j}}{{\left( {{({{V}_{j}})}_{*}} \right)}^{\bot }}\subseteq V$ satisfy 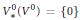 $V_{*}^{0}({{V}^{0}})\,=\,\{0\}$. We then discuss explicit constructions of subspaces
$V_{*}^{0}({{V}^{0}})\,=\,\{0\}$. We then discuss explicit constructions of subspaces 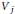 ${{V}_{j}}$ and
${{V}_{j}}$ and 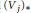 ${{({{V}_{j}})}_{*}}$ as above. Our second main result claims that a Cartan subalgebra of
${{({{V}_{j}})}_{*}}$ as above. Our second main result claims that a Cartan subalgebra of 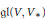 $\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ can be described alternatively as a locally nilpotent self-normalizing subalgebra whose adjoint representation is locally finite, or as a subalgebra
$\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$ can be described alternatively as a locally nilpotent self-normalizing subalgebra whose adjoint representation is locally finite, or as a subalgebra 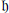 $\mathfrak{h}$ which coincides with the maximal locally nilpotent
$\mathfrak{h}$ which coincides with the maximal locally nilpotent 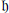 $\mathfrak{h}$-submodule of
$\mathfrak{h}$-submodule of 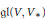 $\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$, and such that the adjoint representation of
$\mathfrak{g}\mathfrak{l}(V,{{V}_{*}})$, and such that the adjoint representation of 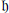 $\mathfrak{h}$ is locally finite.
$\mathfrak{h}$ is locally finite.