Consider the following second-order differential operator:

$$ \begin{align*} T = \frac{1}{2} \sum\limits_{ \genfrac{}{}{0pt}{}{\scriptstyle a+b = p+ q} {\scriptstyle a,b,p,q \geq 1}} x_a x_b \frac{\partial}{\partial x_p} \frac{\partial}{\partial x_q} \end{align*} $$

acting on the Fock space ${\mathcal F} = {\mathbb R} [x_1, x_2, x_3, \ldots ]$ . Similar higher-order operators occur in the study of vertex operator algebras, soliton PDEs, and conformal field theory [Reference Bais, Bouwknegt, Surridge and Schoutens1–Reference Eguchi and Yang3, Reference Sasaki and Yamanaka8].

The Fock space ${\mathcal F}$ has two natural ${\mathbb Z}$ -gradings, by degree, with deg $(x_k) = k$ , and by length, with len $(x_k) = 1$ . Note that the two gradings are given by the eigenspaces of two operators, whose eigenvalues are degree and length, respectively:

$$ \begin{align*} \sum\limits_{k\geq 1} k x_k \frac{\partial}{\partial x_k} \quad\text{and}\quad \sum\limits_{k\geq 1} x_k \frac{\partial}{\partial x_k}. \end{align*} $$

We can decompose ${\mathcal F}$ into a direct sum according to these gradings:

$$ \begin{align*} {\mathcal F} = \mathop\oplus\limits_{d \geq \ell \geq 0} {\mathcal F} (d, \ell), \end{align*} $$

where ${\mathcal F} (d, \ell )$ is the span of all monomials of degree d and length $\ell $ .

Because operator T preserves both gradings, the subspaces ${\mathcal F} (d, \ell )$ are T-invariant. Rather surprisingly, the eigenvalues of T on ${\mathcal F} (d, \ell )$ appear to be nonnegative integers. For example, the spectrum of T on ${\mathcal F} (12,4)$ is

$$ \begin{align*} [1, 3, 3, 5, 6, 7, 7, 10, 10, 10, 13, 15, 17, 19, 30]. \end{align*} $$

The goal of this note is to shed light on the pattern of the eigenvalues of T. Even though this work began as a purely curiosity-driven research, we are going to see that it led to new interesting results on bihomogeneous symmetric functions. We determine algebraic relations between elementary bihomogeneous symmetric functions (Lemma 4) and construct bases in the spaces of such functions (Theorem 3).

The space ${\mathcal F}$ may be viewed as the space of symmetric functions in variables $t_1, t_2, t_3, \ldots $ . Recall that power symmetric functions are

$$ \begin{align*} p_k = \sum_{i \geq 1} t_i^k, \quad k\geq 1. \end{align*} $$

Then, the algebra of symmetric functions is freely generated by $p_1, p_2, p_3, \ldots $ , and may be identified with ${\mathcal F}$ via $x_k = \frac {p_k}{k}$ . We refer to [Reference Macdonald5] for the basic properties of symmetric functions that we review here.

Recall also the definitions of the elementary symmetric functions $e_k$ and complete symmetric functions $h_k$ :

$$ \begin{align*} e_k = \sum\limits_{i_1 < i_2 < \ldots < i_k} t_{i_1} t_{i_2} \ldots t_{i_k}, \quad h_k = \sum\limits_{i_1 \leq i_2 \leq \ldots \leq i_k} t_{i_1} t_{i_2} \ldots t_{i_k}. \end{align*} $$

Introducing the generating series

$$ \begin{align*} e(z) = 1 + \sum_{k=1}^\infty e_k z^k, \quad h(z) = 1 + \sum_{k=1}^\infty h_k z^k, \end{align*} $$

one can relate elementary and complete symmetric functions to power symmetric functions via

(1) $$ \begin{align} h(z) = \exp \left( \sum_{k=1}^\infty \frac{p_k}{k} z^k \right) = \exp \left( \sum_{k=1}^\infty x_k z^k \right), \end{align} $$

(2) $$ \begin{align} e(z) = \exp \left( \sum_{k=1}^\infty (-1)^{k+1} \frac{p_k}{k} z^k \right) = h(-z)^{-1}. \end{align} $$

With respect to the two gradings on the Fock space, the power symmetric function $p_k$ has degree k and length $1$ . It follows from (1) and (2) that $h_k$ and $e_k$ have both degree k, but these functions are not homogeneous with respect to the grading given by length. Let us consider decompositions of elementary and complete symmetric functions into bihomogeneous components. In order to do that, we introduce the generating series

(3) $$ \begin{align} h (r, z) = \exp \left( r \sum_{j=1}^\infty x_j z^j \right) = 1 + \sum_{d \geq \ell \geq 1} g(d, \ell) r^\ell z^d . \end{align} $$

Then,

$$ \begin{align*} h_k = \sum_{\ell \leq k} g(k, \ell), \quad e_k = \sum_{\ell \leq k} (-1)^{k+\ell} g(k, \ell). \end{align*} $$

Note that $g(d, \ell ) \in {\mathcal F} (d, \ell )$ . We shall see below that $g(d, \ell )$ is an eigenfunction for T which corresponds to the dominant eigenvalue on ${\mathcal F} (d, \ell )$ . Our plan is to calculate the spectrum of T by constructing a bihomogeneous basis of the algebra of symmetric functions which consists of the products of functions $g(d, \ell )$ .

Another eigenvalue problem for differential operators with origins in invariant theory and representation theory was studied in [Reference Kostant and Sahi4, Reference Sahi6, Reference Sahi and Salmasian7].

We begin by showing that T is diagonalizable.

Proof Introduce a positive-definite scalar product on ${\mathbb R} [x]$ with $\left < x^n, x^m \right> = n! \delta _{n,m}$ . It is easy to check that this scalar product satisfies

$$ \begin{align*}\left< \frac{d}{dx} f(x), g(x) \right> = \bigg< f(x), x g(x) \bigg> .\end{align*} $$

Viewing ${\mathcal F}$ as a tensor product of infinitely many copies of ${\mathbb R}[x]$ , ${\mathcal F} = {\mathbb R} [x_1] \otimes {\mathbb R} [x_2] \otimes \ldots $ , we obtain a positive-definite scalar product on ${\mathcal F}$ for which $\frac {\partial }{\partial x_k}$ is adjoint to multiplication by $x_k$ . Then, for $f, g \in {\mathcal F}$

$$ \begin{align*} \left< \sum\limits_{ a+b = p+ q} x_a x_b \frac{\partial}{\partial x_p} \frac{\partial}{\partial x_q} f , g \right> = \left< f, \sum\limits_{ a+b = p+ q} x_q x_p \frac{\partial}{\partial x_b} \frac{\partial}{\partial x_a} g \right>, \end{align*} $$

and hence, T is a self-adjoint operator. Thus, T is diagonalizable on each invariant subspace ${\mathcal F} (d, \ell )$ with real eigenvalues.

Because

$$ \begin{align*} \left< Tf, f \right> = \frac{1}{2} \sum_{n=2}^\infty \left< \sum_{p+q = n} \frac{\partial}{\partial x_p} \frac{\partial}{\partial x_q} f , \sum_{a+b = n} \frac{\partial}{\partial x_b} \frac{\partial}{\partial x_a} f \right> \geq 0, \end{align*} $$

the eigenvalues of T are nonnegative. ▪

The dimension of ${\mathcal F} (d, \ell )$ is equal to the number of partitions of d with exactly $\ell $ parts. Each such partition may be presented as a Young diagram $\Lambda $ ; for example, the following diagram represents a partition $28 = 7 + 7 + 5 + 4 + 3 + 2$ with $d = 28$ and $\ell = 6$ . Parameter $\ell $ is the number of rows in $\Lambda $ , whereas d is the total number of boxes in $\Lambda $ .

Let k be the number of the diagonal boxes in $\Lambda $ (shaded boxes in Figure 1). For each diagonal box, consider its hook, the boxes in its row to the right of the diagonal box, the boxes in its column below the diagonal box, together with the diagonal box itself. In addition, consider the leg of a diagonal box, the boxes in its column together with the diagonal box itself.

Figure 1 Young diagram.

In Figure 2, we show the hook and the leg corresponding to the second diagonal box in the above Young diagram $\Lambda $ .

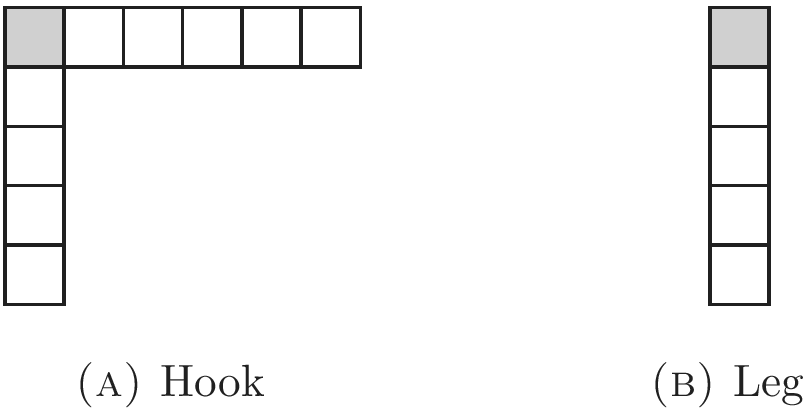
Figure 2 Hook and leg.

The hook number $d_i$ and the leg number $q_i$ of a diagonal box are the numbers of boxes in its hook and leg, respectively. For the Young diagram $\Lambda $ above, the hook and the leg numbers $(d_i, q_i)$ , $i =1, \ldots , k$ , are $(12, 6), (10, 5), (5,3), (1,1)$ .

Note that our definition of the leg number is not quite standard, usually the diagonal box is not included in its leg.

If we denote by $a_i$ the number of boxes in the ith row of $\Lambda $ to the right of the diagonal box, and by $b_i$ the number of boxes in the ith column of $\Lambda $ below the diagonal box, we get the Frobenius presentation of a partition: $(a_1 \ldots a_k | b_1 \ldots b_k)$ .

The hook and leg numbers satisfy $\sum \limits _{i=1}^k d_i = d$ , $q_1 = \ell $ , $d_i - q_i> d_{i+1} - q_{i+1}$ , for $i < k$ .

To each diagonal box, we also assign its leg increment $\ell _i = q_i - q_{i+1}$ , where $q_{k+1}$ is taken to be $0$ . For the Young diagram in Figure 1, $\ell _1 = 1$ , $\ell _2 = 2$ , $\ell _3 = 2$ , $\ell _4 = 1$ . Leg increments satisfy

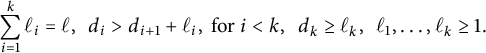(4) $$ \begin{align} \sum_{i=1}^k \ell_i = \ell, \ \ d_i > d_{i+1} + \ell_i, {\text{ for }} i< k, \ \ d_k \geq \ell_k, \ \ \ell_1, \ldots, \ell_k \geq 1. \end{align} $$

Note that there is a bijective correspondence between Young diagrams with $\ell $ rows and sequences $(d_1, \ell _1), \ldots , (d_k, \ell _k)$ satisfying (4).

Theorem 3 The set $S(d,\ell )$ of polynomials $ g(d_1, \ell _1) g(d_2, \ell _2) \ldots g(d_k, \ell _k)$ satisfying conditions

$$ \begin{align*} \sum_{i=1}^k d_i = d, \ \ \sum_{i=1}^k \ell_i = \ell, \ \ d_i > d_{i+1} + \ell_i, \ {\textit{ for }} i< k, \ \ d_k \geq \ell_k , \ \ \ell_1, \ldots, \ell_k \geq 1, \end{align*} $$

forms a basis of ${\mathcal F} (d, \ell )$ , for $d \geq \ell \geq 1$ .

Let $\ell ^\prime , \ell ^{\prime \prime } \geq 1$ . The products $g(d^\prime ,\ell ^\prime ) g(d^{\prime \prime }, \ell ^{\prime \prime })$ with $d^{\prime \prime } + \ell ^\prime \geq d^\prime \geq d^{\prime \prime }$ will be called irregular, whereas the products with $d^\prime> d^{\prime \prime } + \ell ^\prime $ will be called regular. Here, we set $g(0,0) = 1$ and consider $g(d, \ell ) g(0, 0)$ with $d \geq \ell \geq 1$ to be a regular product.

The proof of Theorem 3 will be based on the following lemma.

Proof We will consider the case when $d = d^\prime + d^{\prime \prime }$ is odd and $\ell = \ell ^\prime + \ell ^{\prime \prime }$ is even, $d = 2n+1$ , $\ell = 2m$ . The cases of other parities are analogous. We can write $d^\prime = n + p$ , $d^{\prime \prime } = n - p + 1$ , $2p - 1 \leq \ell ^\prime \leq 2m - 1$ , $\ell ^{\prime \prime } = 2m - \ell ^\prime $ , $1 \leq p \leq m$ .

We will use a decreasing induction in p. As a basis of induction, we may choose $p = m + 1$ , in which case all products are regular and there is nothing to prove. Let us carry out the step of induction. We assume that the claim of the lemma holds for irregular products $g(d_1, \ell _1) g(d_2, \ell _2)$ with $d_1> d^\prime $ .

Consider the generating function

(5) $$ \begin{align} \left[ \prod_{i=1}^{2p-1} \left( z \frac{d}{dz} + p - n - i \right) \prod_{{\scriptstyle j=2p-1}\atop{\scriptstyle j\neq \ell^\prime}}^{2m-1} \left( r \frac{d}{dr} - j \right) h(r,z) \right] h(-r, z) . \end{align} $$

Because

$$ \begin{align*} r \frac{d}{dr} h(r,z) = r \left( \sum_{j=1}^\infty x_j z^j \right) h(r, z),\quad z \frac{d}{dz} h(r,z) = r \left( \sum_{j=1}^\infty j x_j z^j \right) h(r, z) \end{align*} $$

and $h(-r,z) = h(r,z)^{-1}$ , we see that (5) is a polynomial in r. Because the total number of derivatives is $\ell -1$ , it is in fact a polynomial in r of degree $\ell - 1$ . Hence, the coefficient at $z^d r^\ell $ in (5) is equal to $0$ . Expanding $h(r,z)$ and $h(-r,z)$ as in (3), and extracting the coefficient at $z^d r^\ell $ , we get an identity

(6) $$ \begin{align} \sum_{{\scriptstyle d_1 + d_2 = d} \atop {\scriptstyle \ell_1 + \ell_2 = \ell}} (-1)^{\ell_2} \prod_{i=1}^{2p-1} \left( d_1 + p - n - i \right) \prod_{{\scriptstyle j=2p-1}\atop{\scriptstyle j\neq \ell^\prime}}^{2m-1} \left( \ell_1 - j \right) g(d_1, \ell_1) g(d_2, \ell_2) = 0. \end{align} $$

Note that the terms in (6) with $n-p+1 \leq d_1 \leq n+p-1$ vanish. If $d_1> n+p-1$ , then $d_1 \geq d^\prime $ , and in case when $d_1 < n - p +1$ , we get $d_2> d^\prime $ . If we look at the terms in (6) with $d_1 = d^\prime $ , all such irregular terms will vanish due to factors $(\ell _1 - j)$ , except for $g(d^\prime ,\ell ^\prime ) g(d^{\prime \prime }, \ell ^{\prime \prime })$ . Thus, we can use (6) to express $g(d^\prime ,\ell ^\prime ) g(d^{\prime \prime }, \ell ^{\prime \prime })$ as a linear combination of regular products and those irregular products for which the claim of the lemma holds by the induction assumption. All regular products in the expansion of $g(d^\prime ,\ell ^\prime ) g(d^{\prime \prime }, \ell ^{\prime \prime })$ will have $d_1> d^\prime $ or $d_1 = d^\prime $ and $\ell _1 < \ell ^\prime $ . This completes the proof of the lemma. ▪

Let us order the set of pairs $(d, \ell )$ as follows: $(d_1, \ell _1) \succ (d_2, \ell _2)$ if either $d_1> d_2$ or $d_1 = d_2$ and $\ell _1 < \ell _2$ . Consider the set ${\widehat S} (d, \ell )$ of ordered products $g(d_1, \ell _1) g(d_2, \ell _2) \ldots g(d_k, \ell _k)$ with $(d_1, \ell _1) \succeq (d_2, \ell _2) \succeq \cdots \succeq (d_k, \ell _k)$ , $\sum \limits _{i=1}^k d_i = d$ , $\sum \limits _{i=1}^k \ell _i = \ell $ , $\ell _i \geq 1$ . Introduce a lexicographic order on ${\widehat S} (d, \ell )$ :

$$ \begin{align*}g(d^\prime_1, \ell^\prime_1) g(d^\prime_2, \ell^\prime_2) \ldots g(d^\prime_k, \ell^\prime_k) \succ g(d^{\prime\prime}_1, \ell^{\prime\prime}_1) g(d^{\prime\prime}_2, \ell^{\prime\prime}_2) \ldots g(d^{\prime\prime}_k, \ell^{\prime\prime}_k)\end{align*} $$

if for some m, $(d^\prime _i, \ell ^\prime _i) = (d^{\prime \prime }_i, \ell ^{\prime \prime }_i)$ , for $i = 1, \ldots , m-1,$ and $(d^\prime _m, \ell ^\prime _m) \succ (d^{\prime \prime }_m, \ell ^{\prime \prime }_m)$ .

Now, we can prove Theorem 3. The set ${\widehat S} (d, \ell )$ clearly spans the space ${\mathcal F} (d, \ell )$ , because $g(p, 1) = x_p$ and ${\mathcal F} (d, \ell )$ is spanned by monomials. It follows from Lemma 4 that every product from ${\widehat S} (d, \ell )$ , which is not in $S(d, \ell )$ may be expressed as a linear combination of the elements of ${\widehat S} (d, \ell )$ which are greater in the lexicographic order. By induction with respect to this ordering, we conclude that

$$ \begin{align*} {\mathcal F} (d, \ell) = \text{ Span}\; {\widehat S} (d, \ell) = \text{Span}\; S(d,\ell) . \end{align*} $$

However, elements of $S(d, \ell )$ are parameterized by Young diagrams with d boxes and $\ell $ rows. Hence, $|S(d, \ell )| = {\text { dim}}\; {\mathcal F}(d, \ell )$ , and $S(d, \ell )$ is a basis of ${\mathcal F}(d, \ell )$ . This completes the proof of Theorem 3.

Let us compute the eigenvalues of the differential operator T.

Theorem 5 Eigenvalues of the operator

$$ \begin{align*} T = \frac{1}{2} \sum\limits_{ {\scriptstyle a+b = p+ q} \atop {\scriptstyle a,b,p,q \geq 1}} x_a x_b \frac{\partial}{\partial x_p} \frac{\partial}{\partial x_q} \end{align*} $$

on ${\mathcal F} (d, \ell )$ , $\ell \geq 1$ , are parameterized by sequences $(d_1, \ell _1), (d_2, \ell _2), \ldots , (d_k, \ell _k)$ with

$$ \begin{align*} d_i > d_{i+1} + \ell_i, \ i = 1, \ldots, k-1, \ \ d_k \geq \ell_k, \ \ \sum\limits_{i=1}^k d_i = d, \ \ \sum\limits_{i=1}^k \ell_i = \ell, \ \ \ell_1, \ldots, \ell_k \geq 1. \end{align*} $$

The corresponding eigenvalue is

$$ \begin{align*} \lambda = \frac{1}{2} \sum_{i=1}^k (\ell_i -1) (2 d_i - \ell_i) . \end{align*} $$

Proof We are going to show that the matrix of the operator T is upper-triangular in the basis $S(d, \ell )$ ordered by $\succ $ . Then, the spectrum of T is given by the diagonal of this matrix.

Consider the generating functions

$$ \begin{align*} X_i = r_i \sum_{j=1}^\infty x_j z_i^j \end{align*} $$

and

$$ \begin{align*} E = \exp \left( \sum_{i=1}^\infty X_i \right) = \exp \left( \sum_{i=1}^\infty r_i \sum_{j=1}^\infty x_j z_i^j \right) . \end{align*} $$

The product $g(d_1, \ell _1) \ldots g(d_k, \ell _k)$ is the coefficient at $z_1^{d_1} \ldots z_k^{d_k} r_1^{\ell _1} \ldots r_k^{\ell _k}$ in E. Let us apply operator T to the generating function E:

$$ \begin{align*} TE &= \frac{1}{2} \sum_{n=2}^\infty \left( \sum_{a+b = n} x_a x_b \right) \sum_{p+q = n} \frac{\partial}{\partial x_p}\frac{\partial}{\partial x_q} E \\ & = \frac{1}{2} \sum_{n=2}^\infty \left( \sum_{a+b = n} x_a x_b \right) \sum_{p+q = n} \left( \sum_{i=1}^\infty r_i z_i^p \right) \left( \sum_{j=1}^\infty r_j z_j^q \right) E \\ &= \frac{1}{2} \sum_{i=1}^\infty r_i^2 \sum_{n=2}^\infty \left( \sum_{a+b = n} x_a x_b \right) \sum_{p+q = n} z_i^{p+q} E \\ & \quad + \sum_{i < j} r_i r_j \sum_{n=2}^\infty \left( \sum_{a+b = n} x_a x_b \right) \sum_{p+q = n} z_i^p z_j^q E \\ & = \frac{1}{2} \sum_{i=1}^\infty r_i^2 \sum_{n=2}^\infty \left( \sum_{a+b = n} x_a x_b \right) (n-1) z_i^n E \\ & \quad + \sum_{i < j} r_i r_j \sum_{n=2}^\infty \left( \sum_{a+b = n} x_a x_b \right) \left( 1 - \frac{z_j}{z_i} \right)^{-1} \left( z_j z_i^{n-1} - z_j^n \right) E \\ & = \frac{1}{2} \sum_{i=1}^\infty \left[ \left( z_i \frac{d}{dz_i} - 1 \right) r_i^2 \sum_{a, b \geq 1} x_a x_b z_i^{a + b} \right] E \\ & \quad - \sum_{i < j} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_i}{r_j} r_j^2 \sum_{a,b \geq 1} \left( x_a x_b z_j^{a+b} \right) E \\ & \quad + \sum_{i < j} \frac{z_j}{z_i} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_j}{r_i} r_i^2 \sum_{a,b \geq 1} \left( x_a x_b z_i^{a+b} \right) E \\ & = \frac{1}{2} \sum_{i=1}^\infty \left[ \left( z_i \frac{d}{d z_i} -1 \right) X_i^2 \right] E - \sum_{i < j} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_i}{r_j} X_j^2 E + \sum_{i < j} \frac{z_j}{z_i} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_j}{r_i} X_i^2 E \\ & = \sum_{i=1}^\infty \left[ \left( z_i \frac{d}{d z_i} - \frac{1}{2} \right) X_i \right] X_i E - \sum_{i < j} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_i}{r_j} X_j^2 E + \sum_{i < j} \frac{z_j}{z_i} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_j}{r_i} X_i^2 E \\ & = \sum_{i=1}^\infty \left[ \left( z_i \frac{d}{d z_i} - \frac{1}{2} \right) X_i \right] r_i \frac{d}{dr_i} E \\ & \quad - \sum_{i < j} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_i}{r_j} X_j r_j \frac{d}{dr_j} E + \sum_{i < j} \frac{z_j}{z_i} \left( 1 - \frac{z_j}{z_i} \right)^{-1} \frac{r_j}{r_i} X_i r_i \frac{d}{dr_i} E \\ & = \sum_{i=1}^\infty \left( r_i \frac{d}{dr_i} - 1\right) \left[ z_i \frac{d}{d z_i} X_i - \frac{1}{2} X_i \right] E \\ & \quad - \sum_{i < j} \left( 1 - \frac{z_j}{z_i} \right)^{-1} r_j \frac{d}{dr_j} \frac{r_i}{r_j} X_j E + \sum_{i < j} \frac{z_j}{z_i} \left( 1 - \frac{z_j}{z_i} \right)^{-1} r_i \frac{d}{dr_i} \frac{r_j}{r_i} X_i E \\ & = \sum_{i=1}^\infty \left( r_i \frac{d}{dr_i} - 1\right) \left( z_i \frac{d}{d z_i} - \frac{1}{2} r_i \frac{d}{dr_i} \right) E \\ & \quad - \sum_{i < j} \left( 1 - \frac{z_j}{z_i} \right)^{-1} r_j \frac{d}{dr_j} \frac{r_i}{r_j} r_j \frac{d}{dr_j} E + \sum_{i < j} \frac{z_j}{z_i} \left( 1 - \frac{z_j}{z_i} \right)^{-1} r_i \frac{d}{dr_i} \frac{r_j}{r_i} r_i \frac{d}{dr_i} E . \end{align*} $$

To get the formula for the action of T on the elements of $S(d, \ell )$ , we extract the coefficient at $z_1^{d_1} \ldots z_k^{d_k} r_1^{\ell _1} \ldots r_k^{\ell _k}$ in $TE$ :

$$ \begin{align*} & T g(d_1, \ell_1) g(d_2, \ell_2) \ldots g(d_k, \ell_k) \\ & \quad = \sum_{i=1}^k (\ell_i -1) \left( d_i - \frac{\ell_i}{2} \right) g(d_1, \ell_1) g(d_2, \ell_2) \ldots g(d_k, \ell_k) \\ & \qquad - \sum_{i < j} \sum_{p=0}^\infty \ell_j (\ell_j + 1) g(d_1, \ell_1) \ldots g(d_i+p, \ell_i - 1) \ldots g(d_j - p, \ell_j + 1) \ldots g(d_k, \ell_k) \\ & \qquad + \sum_{i < j} \sum_{p=1}^\infty \ell_i (\ell_i + 1) g(d_1, \ell_1) \ldots g(d_i+p, \ell_i + 1) \ldots g(d_j - p, \ell_j - 1) \ldots g(d_k, \ell_k) . \end{align*} $$

The first part in the above expression yields the diagonal part of T with the eigenvalue $\lambda = \frac {1}{2} \sum \limits _{i=1}^k (\ell _i -1) (2 d_i - \ell _i)$ , while the last two sums, when expanded in the basis $S(d, \ell )$ applying Lemma 4 whenever necessary, only contain terms that are strictly greater than $g(d_1, \ell _1) g(d_2, \ell _2) \ldots g(d_k, \ell _k)$ with respect to the lexicographic order $\succ $ . This completes the proof of the theorem. ▪

It follows from the proof of Theorem 5 that $g(d, \ell )$ is the eigenfunction for the operator T with the eigenvalue $\lambda = \frac {1}{2} (\ell -1) (2 d - \ell )$ , which is the dominant eigenvalue on ${\mathcal F} (d, \ell )$ .

We observe that $0$ is an eigenvalue of T on ${\mathcal F} (d, \ell )$ if and only if $d \geq \ell ^2$ .

We can obtain an orthogonal basis of eigenfunctions for T in ${\mathcal F}(d,\ell )$ from the ordered basis $S(d, \ell )$ using the Gram–Schmidt procedure.

It was pointed out by the referee of this paper that the eigenvalue of T corresponding to a given partition may be written using its Frobenius presentation in the following form:

$$ \begin{align*}\lambda = \frac{\ell (\ell - 1)}{2} + \sum_{i=1}^k a_i b_i - \sum_{i=1}^{k-1} (a_i + 1)(b_{i+1} + 1).\end{align*} $$

In conclusion, we list in Table 1 eigenfunctions of T corresponding to partitions with $d \leq 7$ . We only present these for spaces ${\mathcal F} (d, \ell )$ of dimension greater than 1. We normalize the eigenfunctions in a way to make the coefficients to be relatively prime integers. As a result, listed symmetric functions are orthogonal to each other but do not have norm 1. For each pair $(d ,\ell )$ , partitions are listed in a decreasing order with respect to linear order $\succ $ .

Table 1:

We recall that, in our notations, $x_k = p_k / k$ , where $p_k$ is the power symmetric function.