Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T05:45:16.683Z Has data issue: false hasContentIssue false
  • English
  • Français

Auerbach Bases and Minimal Volume Sufficient Enlargements

Published online by Cambridge University Press:  20 November 2018

M. I. Ostrovskii
M. I. Ostrovskii*
Affiliation:
Department of Mathematics and Computer Science, St. John's University, Queens, NY 11439, U.S.A.e-mail: ostrovsm@stjohns.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 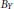${{B}_{Y}}$ denote the unit ball of a normed linear space $Y$. A symmetric, bounded, closed, convex set 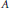$A$ in a finite dimensional normed linear space $X$ is called a sufficient enlargement for $X$ if, for an arbitrary isometric embedding of $X$ into a Banach space $Y$, there exists a linear projection 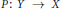$P:\,Y\,\to \,X$ such that 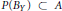$P({{B}_{Y}})\,\subset \,A$. Each finite dimensional normed space has a minimal-volume sufficient enlargement that is a parallelepiped; some spaces have “exotic” minimal-volume sufficient enlargements. The main result of the paper is a characterization of spaces having “exotic” minimal-volume sufficient enlargements in terms of Auerbach bases.

Keywords

46B0752A2146B15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 4 , 01 December 2011 , pp. 726 - 738
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Auerbach, H., On the area of convex curves with conjugate diameters (in Polish). Ph. D. thesis, University of Lwów, 1930.Google Scholar
[2] Banach, S., Théorie des opérations linéaires, Monografje Matematyczne I, Warszawa, 1932.Google Scholar
[3] Day, M. M., Polygons circumscribed about closed convex curves.. Trans. Amer. Math. Soc. 62(1947), 315–319.Google Scholar
[4] Erdahl, R. M., Zonotopes, dicings, and Voronoi's conjecture on parallelohedra. European J. Combin. 20(1999), no. 6, 527–549. doi:10.1006/eujc.1999.0294Google Scholar
[5] Gordon, Y., Meyer, M., and Pajor, A., Ratios of volumes and factorization through ℓ∞ . Illinois J. Math. 40(1996), no. 1, 91–107.Google Scholar
[6] Johnson, W. B. and Lindenstrauss, J., Basic concepts in the geometry of Banach spaces. In: Handbook of the geometry of Banach spaces, 1, North-Holland, Amsterdam, 2001, pp. 1–84.Google Scholar
[7] McMullen, P., Space tiling zonotopes. Mathematika 22(1975), no. 2, 202–211. doi:10.1112/S0025579300006082Google Scholar
[8] Orrick, W. P. and Solomon, B., Large-determinant sign matrices of order 4k + 1 . Discrete Math. 307(2007), no. 2, 226–236. doi:10.1016/j.disc.2006.04.041Google Scholar
[9] Ostrovskii, M. I., Generalization of projection constants: sufficient enlargements. Extracta Math. 11(1996), no. 3, 466–474.Google Scholar
[10] Ostrovskii, M. I., Projections in normed linear spaces and sufficient enlargements. Arch. Math. (Basel) 71(1998), no. 4, 315–324.Google Scholar
[11] Ostrovskii, M. I., Minimal-volume projections of cubes and totally unimodular matrices.. Linear Algebra Appl. 364(2003), 91–103. doi:10.1016/S0024-3795(02)00539-6Google Scholar
[12] Ostrovskii, M. I., Sufficient enlargements of minimal volume for two-dimensional normed spaces. Math. Proc. Cambridge Philos. Soc. 137(2004), no. 2, 377–396. doi:10.1017/S0305004104007819Google Scholar
[13] Ostrovskii, M. I., Sufficient enlargements of minimal volume for finite-dimensional normed linear spaces. J. Funct. Anal. 255(2008), no. 3, 589–619. doi:10.1016/j.jfa.2008.04.012Google Scholar
[14] Ostrovskii, M. I., Sufficient enlargements in the study of projections in normed linear spaces. Indian J. Math. 2008, suppl, 105–122.Google Scholar
[15] Pełczyński, A. and Szarek, S. J., On parallelepipeds of minimal volume containing a convex symmetric body in ℝ n . Math. Proc. Cambridge Phil. Soc. 109(1991), no. 1, 125–148. doi:10.1017/S0305004100069619Google Scholar
[16] Plichko, A. M., On the volume method in the study of Auerbach bases of finite-dimensional normed spaces. Colloq. Math. 69(1995), no. 2, 267–270.Google Scholar
[17] Schneider, R., Convex Bodies: the Brunn–Minkowski theory. In: Encyclopedia of Mathematics and its Applications, 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[18] Taylor, A. E., A geometric theorem and its application to biorthogonal systems.. Bull. Amer. Math. Soc. 53(1947), 614–616. doi:10.1090/S0002-9904-1947-08855-8Google Scholar