Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T11:50:39.805Z Has data issue: false hasContentIssue false
  • English
  • Français

W-Groups under Quadratic Extensions of Fields

Published online by Cambridge University Press:  20 November 2018

Ján Mináč  and
Tara L. Smith
Ján Mináč
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ontario, N6A 5B7 email: minac@uwo.ca
Tara L. Smith
Affiliation:
Department of Mathematical Sciences, University of Cincinnati, Cincinnati, Ohio 45221-0025, USA email: tara.smith@math.uc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To each field 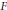$F$ of characteristic not 2, one can associate a certain Galois group 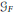${{\mathcal{G}}_{F}}$, the so-called 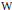$\text{W}$-group of 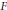$F$, which carries essentially the same information as the Witt ring 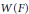$W(F)$ of 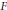$F$. In this paper we investigate the connection between 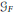${{\mathcal{G}}_{F}}$ and 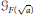${{\mathcal{G}}_{F(\sqrt{a})}}$, where $F(\sqrt{a})$ is a proper quadratic extension of 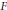$F$. We obtain a precise description in the case when 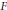$F$ is a pythagorean formally real field and 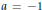$a=-1$, and show that the 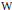$\text{W}$-group of a proper field extension 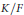$K/F$ is a subgroup of the 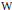$\text{W}$-group of 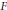$F$ if and only if 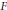$F$ is a formally real pythagorean field and 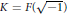$K=F(\sqrt{-1)}$. This theorem can be viewed as an analogue of the classical Artin-Schreier’s theorem describing fields fixed by finite subgroups of absolute Galois groups. We also obtain precise results in the case when $a$ is a double-rigid element in 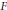$F$. Some of these results carry over to the general setting.

Keywords

11E8112D15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 4 , 01 August 2000 , pp. 833 - 848
Copyright
Copyright © Canadian Mathematical Society 2000

References

[AKM] Adem, A., Karagueuzian, D. and Mináč, J., On the cohomology of Galois groups determined byWitt rings. Max Planck Institute Preprint 30, 1998; Adv. Math., to appear.Google Scholar
[Art] Artin, E., Galois theory. Dover Publications, 1998.Google Scholar
[AT] Artin, E. and Tate, J., Class Field Theory. Addison-Wesley, Redwood City, California, 1990.Google Scholar
[Be1] Berman, L., The Kaplansky Radical and Values of Binary Quadratic Forms. PhD thesis, University of California, Berkeley, California, 1978.Google Scholar
[Be2] Berman, L., Quadratic forms and power series fields. Pacific J. Math. 89(1980), 257–267.Google Scholar
[BCW] Berman, L., Cordes, C. and Ware, R., Quadratic forms, rigid elements and formal power series fields. J. Algebra 66(1980), 123–133.Google Scholar
[CSm1] Craven, T. and Smith, T. L., Formally real fields from a Galois theoretic perspective. J. Pure Appl. Algebra 145(2000), 19–36.Google Scholar
[CSm2] Craven, T. and Smith, T. L.,Witt ring quotients associated to subgroups of F/F2. Unpublished manuscript, 1997.Google Scholar
[E] Evens, L., The Cohomology of Groups. Oxford Mathematical Monographs, Oxford University Press, New York, 1991.Google Scholar
[GMi] Gao, W. and Mináč, J., Milnor Conjecture and Galois theory I. Fields Institute Communications 16(1997), 95–110.Google Scholar
[Jac] Jacobson, N., Lectures in Abstract Algebra, Vol. III. Van Nostrand Company, Inc., 1964.Google Scholar
[Ko] Koch, H., Galoissche Theorie der p-Erweiterungen. Springer-Verlag, Berlin, 1970.Google Scholar
[L1] Lam, T. Y., The Algebraic Theory of Quadratic Forms. Benjamin/Cummings Publishing Co., Reading, Mass., 1980.Google Scholar
[L2] Lam, T. Y., Orderings, Valuations and Quadratic Forms. Conference Board of theMathematical Sciences 52, Amer.Math. Soc., Providence, RI, 1983.Google Scholar
[L3] Lam, T. Y., The theory of ordered fields. In: Ring Theory and Algebra III (ed. McDonald, B. R.), Amer. Math. Soc. 55(1980), 1–152.Google Scholar
[MMS] Mahé, L., Mináč, J. and Smith, T., Additive structure of subgroups of F/F2 and Galois theory. In preparation.Google Scholar
[Ma] Marshall, M., Abstract Witt Rings. Queen's Papers in Pure and Appl. Math. 57, Queen's University, Kingston, Ontario, 1980.Google Scholar
[Me] Merkurjev, A., On the norm residue symbol of degree 2. Dokl. Akad. Nauk. SSSR 261(1981), 542–547; English transl. in Soviet Mat. Dokl. 24(1981), 546–551.Google Scholar
[MiSm1] Mináč, J. and Smith, T., W-groups and values of binary forms. J. Pure Appl. Algebra 87(1993), 61–78.Google Scholar
[MiSm2] Mináč, J. and Smith, T., Decomposition of Witt rings and Galois groups. Canad. J. Math 47(1995), 1274–1289.Google Scholar
[MiSp1] Mináč, J. and Spira, M., u = 4 and quadratic extensions. Rocky Mountain J. Math. 19(1989), 833–845.Google Scholar
[MiSp2] Mináč, J. and Spira, M., Formally real fields, pythagorean fields, C-fields and W-groups. Math. Z. 205(1990), 519–530.Google Scholar
[MiSp3] Mináč, J. and Spira, M., Witt rings and Galois groups. Ann. of Math. 144(1996), 35–60.Google Scholar
[Mor] Morris, S. A., Pontrjagin duality and the structure of locally compact abelian groups. LondonMath. Soc. Lecture Note Ser. 29, Cambridge University Press, 1977.Google Scholar
[PSCL] Perlis, R., Szymiczek, K., Conner, P. E. and Litherland, R., Matching Witts with global fields. In: Recent Advances in Real Algebraic Geometry and Quadratic Forms (eds. Jacob, W., Lam, T. Y. and Robson, R. O.), Contemp.Math. 155(1994), 365–387.Google Scholar
[Ser] Serre, J.-P., Galois cohomology. Springer-Verlag, 1997.Google Scholar
[Sc] Scharlau, W., Quadratic and Hermitian Forms. GrundlehrenMath.Wiss. 270, Springer-Verlag, Berlin, 1985.Google Scholar
[Wd] Wadsworth, A., Merkurjev's elementary proof of Merkurjev's theorem. Contemp.Math. 55(1986), 741–776.Google Scholar
[Wa] Ware, R., When are Witt rings group rings? II. Pacific J. Math 76(1978), 541–564.Google Scholar