A variety (primitive class) is a class of abstract algebras which is closed under the formation of subalgebras, homomorphic images, and products. For a given variety 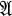we shall call a function μ*, which assigns to each algebra 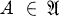a natural number or ∞, denoted by μ*(A), a variety invariant if for every natural number n the class of all 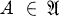with μ*(A) ≦ n is again a variety. In this paper, a general method of finding variety invariants for the variety of all modular lattices will be developed. This method will be based on the concept of a quotient tree of a modular lattice. As examples of variety invariants we shall define, using the general result, the primitive length and the primitive width of modular lattices.