Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-11T16:18:37.263Z Has data issue: false hasContentIssue false
  • English
  • Français

$*$-Subvarieties of the Variety Generated by 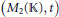$\left( {{M}_{2}}\left( \mathbb{K} \right),\,t \right)$

Published online by Cambridge University Press:  20 November 2018

Francesca Benanti ,
Onofrio M. Di Vincenzo  and
Vincenzo Nardozza
Francesca Benanti
Affiliation:
Dipartimento di Matematica e Applicazioni, via Archirafi 34, 90123 Palermo, Italia, email: fbenanti@dipmat.math.unipa.it
Onofrio M. Di Vincenzo
Affiliation:
Dipartimento Interuniversitario, di Matematica, via Orabona 4, 70125 Bari, Italia, email: divincenzo@dm.uniba.it
Vincenzo Nardozza
Affiliation:
Dipartimento di Matematica e Applicazioni, via Archirafi 34, 90123 Palermo, Italia, email: vickkk@tiscalinet.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 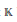$\mathbb{K}$ be a field of characteristic zero, and 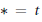$*\,=\,t$ the transpose involution for the matrix algebra 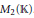${{M}_{2}}\left( \mathbb{K} \right)$. Let 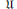$\mathfrak{U}$ be a proper subvariety of the variety of algebras with involution generated by 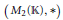$\left( {{M}_{2}}\left( \mathbb{K} \right),\,* \right)$. We define two sequences of algebras with involution 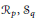${{R}_{p}},\,{{S}_{q}}$, where 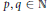$p,\,q\,\in \,\mathbb{N}$. Then we show that 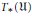${{T}_{*}}\left( \mathfrak{U} \right)$ and 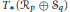${{T}_{*}}\left( {{R}_{p}}\oplus \,{{S}_{q}} \right)$ are $*$-asymptotically equivalent for suitable $p,\,q$.

Keywords

16R1016W1016R50algebras with involutionasymptotic equivalence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 42 - 63
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Drensky, V., Free Algebras and PI-Algebras. Springer-Verlag, Berlin-Heidelberg-Singapore, 2000.Google Scholar
[2] Drensky, V., Polynomial identities of finite dimensional algebras. Serdica 12 (1986), 209–216.Google Scholar
[3] Drensky, V. S. and Giambruno, A., Cocharacters, codimensions and Hilbert series of the polynomial identities for 2 × 2 matrices with involution. Canad. J. Math. 46 (1994), 718–733.Google Scholar
[4] Giambruno, A., GL × GL-representations and *-polynomial identities. Comm. Algebra 14 (1986), 787–796.Google Scholar
[5] Giambruno, A. and Regev, A., Wreath products and P.I. algebras. J. Pure Appl. Algebra 35 (1985), 133–149.Google Scholar
[6] Kemer, A. R., Asymptotic basis of identities of algebras with unit from the variety Var(M2(K)). Soviet Math. (6) 33 (1990), 71–76.Google Scholar
[7] Koshlukov, P. E., Polynomial identities for a family of simple Jordan algebras. Comm. Algebra 16 (1988), 1325–1371.Google Scholar
[8] Procesi, C., Computing with 2 × 2 matrices. J. Algebra 87 (1984), 342–359.Google Scholar
[9] Rowen, L. H., Polynomial Identities in Ring Theory. Academic Press, New York, 1980.Google Scholar