Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T11:04:41.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Subspaces of de Branges Spaces Generated by Majorants

Published online by Cambridge University Press:  20 November 2018

Anton Baranov  and
Harald Woracek
Anton Baranov
Affiliation:
Department of Mathematics and Mechanics, Saint Petersburg State University, 28, Universitetski pr., 198504 St. Petersburg, Russia, a.baranov@ev13934.spb.edu
Harald Woracek
Affiliation:
Institute for Analysis and ScientificComputing, ViennaUniversity of Technology, WiednerHauptstr. 8-10/101, 1040 Vienna, Austria, harald.woracek@tuwien.ac.at
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a given de Branges space $\mathcal{H}(E)$ we investigate de Branges subspaces defined in terms of majorants on the real axis. If $\omega $ is a nonnegative function on $\mathbb{R}$, we consider the subspace

$${{\mathcal{R}}_{\omega }}(E)=\text{Clo}{{\text{s}}_{\mathcal{H}(E)}}\{F\in \mathcal{H}(E):\text{there exists }C>0:|{{E}^{-1}}F|\le C\omega \,on\,\mathbb{R}\}.$$

We show that 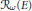${{\mathcal{R}}_{\omega }}(E)$ is a de Branges subspace and describe all subspaces of this form. Moreover, we give a criterion for the existence of positive minimal majorants.

Keywords

46E2030D1546E22Branges subspacemajorantBeurling-Malliavin Theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 503 - 517
Copyright
Copyright © Canadian Mathematical Society 2009

References

[B] Baranov, A. D., Polynomials in the de Branges spaces of entire functions. Ark. Mat. 44(2006), no. 1, 16–38.Google Scholar
[BH] Baranov, A. D. and Havin, V. P., Admissible majorants for model subspaces and arguments of inner functions. Funct. Anal. Appl. 40(2006), no. 4, 249–263.Google Scholar
[BBH] Baranov, A. D., Borichev, A. A., and Havin, V. P., Majorants of meromorphic functions with fixed poles. Indiana Univ. Math. J. 56(2007), no. 4, 1595–1628.Google Scholar
[B M] Beurling, A. and Malliavin, P., On Fourier transforms of measures with compact support. Acta Math. 107(1962), 291–309.Google Scholar
[deB] de Branges, L., Hilbert spaces of entire functions. Prentice Hall, Englewood Cliffs, NJ, 1968.Google Scholar
[GK] Gohberg, I. and Krein, M. G., Theory and applications of Volterra operators in Hilbert space. Translations of Mathematical Monographs 24, American Mathematical Society, Providence, RI, 1970.Google Scholar
[HSW] Hassi, S., De Snoo, H., and Winkler, H., Boundary-value problems for two-dimensional canonical systems. Integral Equations Operator Theor. 36(2000), no. 4, 445–479.Google Scholar
[HJ] Havin, V. and Jöricke, B., The uncertainty principle in harmonic analysis. Springer-Verlag, Berlin, 1994.Google Scholar
[H M1] Havin, V. P. and Mashreghi, J., Admissible majorants for model subspaces of H2. I. Slow winding of the generating inner function. Canad. J. Math. 55(2003), no. 6, 1231–1263.Google Scholar
[H M2] Havin, V. P. and Mashreghi, J., Admissible majorants for model subspaces of H2. II. Fast winding of the generating inner function. Canad. J. Math. 55(2003), no. 6, 1264–1301.Google Scholar
[KW1] Kaltenbäck, M. and Woracek, H., Pontryagin spaces of entire functions I. Integral Equations Operator Theor. 33(1999), no. 1, 34–97.Google Scholar
[KW2] Kaltenbäck, M. and Woracek, H., de Branges spaces of exponential type: general theory of growth. Acta Sci. Math. (Szeged)). 71(2005), no. 1-2, 231–284.Google Scholar
[KW3] Kaltenbäck, M. and Woracek, H., Hermite–Biehler functions with zeros close to the imaginary axis. Proc. Amer. Math. Soc. 133(2005), no. 1, 245–255.Google Scholar
[K] Koosis, P., Lecons sur le thèorème de Beurling et Malliavin. Les Publications CR M, Montrèal, QC, 1996.Google Scholar
[MNH] Mashreghi, J., Nazarov, F., and Havin, V. P., Beurling– Malliavin multiplier theorem: the seventh proof. St. Petersburg Math. J. 17(2006), no. 5, 699–744.Google Scholar
[RR] Rosenblum, M. and Rovnyak, J., Topics in Hardy classes and univalent functions. Birkhäuser Verlag, Basel, 1994.Google Scholar
[R] Rudin, W., Functional Analysis. Second edition, International Series in Pure and Applied Mathematics, McGraw-Hill, New York, 1991.Google Scholar
[W] H.Woracek, de Branges spaces of entire functions closed under forming difference quotients. Integral Equations Operator Theor. 37(2000), no 2, 238–249.Google Scholar