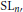Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T02:33:25.705Z Has data issue: false hasContentIssue false
  • English
  • Français

$S{{L}_{n\prime }}$ Orthogonality Relations and Transfer

Published online by Cambridge University Press:  20 November 2018

Alexandru Ioan Badulescu
Alexandru Ioan Badulescu*
Affiliation:
86034 Poitiers Cedex, Université de Poitiers, France email: badulescu@mathlabo.univ-poitiers.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\pi $ be a square integrable representation of 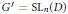${G}'=\text{S}{{\text{L}}_{n}}(D)$, with 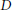$D$ a central division algebra of finite dimension over a local field $F$of non-zero characteristic. We prove that, on the elliptic set, the character of $\pi $ equals the complex conjugate of the orbital integral of one of the pseudocoefficients of $\pi $. We prove also the orthogonality relations for characters of square integrable representations of 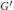${G}'$. We prove the stable transfer of orbital integrals between 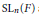$\text{S}{{\text{L}}_{n}}(F)$ and its inner forms.

Keywords

20G05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 3 , 01 June 2007 , pp. 449 - 464
Copyright
Copyright © Canadian Mathematical Society 2007

References

[Ba1] Badulescu, A. I., Orthogonalité des caractères pou. GL n sur un corps local de caractéristique non nulle. Manuscripta Math. 101(2002), no. 1, 49–70.Google Scholar
[Ba2] Badulescu, A. I., Correspondance de Jacquet-Langlands pour les corps locaux de caractéristique non nulle. Ann. Sci. é cole Norm. Sup. 35(2002), no. 5, 695–747.Google Scholar
[Ba3] Badulescu, A. I., Un résultat de transfert et un résultat d’intégrabilité locale des caractères en caractéristique non nulle. J. Reine Angew.Math. 595(2003), 101–124.Google Scholar
[Be] Bernstein, J., Le “centre” de Bernstein. In: Représentations des groupes réductifs sur un corps local, Herman, Paris 1984.Google Scholar
[BS] Borevich, Z. I. and Shafarevich, I. R., Number Theory. Pure and Applied Mathematic 20, Academic Press, New York, 1966.Google Scholar
[Cl] Clozel, L., Invariant harmonic analysis on the Schwarz space of a reductive p-adic group. In: Harmonic Analysis on Reductive Groups, Prog. Math. 101, Birkhäuser Boston, Boston, 1991, pp. 101–121.Google Scholar
[DKV] Deligne, P., Kazhdan, D., and Vignéras, M.-F., Représentations des algèbres centrales simples p-adiques. In: Représentations des groupes réductifs sur un corps local, Herman, Paris 1984.Google Scholar
[Ka] Kazhdan, D., Representations of groups over close local fields. J. Analyse Math. 47(1986), 175–179.Google Scholar
[LL] Labesse, J. P. and Langlands, R. P., L-indistinguishability for SL(2). Canad. J. Math. 31(1979), no. 4, 726–785.Google Scholar
[Le1] Lemaire, B., Intégrales orbitales sur GL(N. et corps locaux proches. Ann. Inst. Fourier (Grenoble) 46(1996), no. 4, 1027–1056.Google Scholar
[Le2] Lemaire, B., Intégrabilité locale des caractères de SL n (D). Pacific J. Math. 222(2005), no. 1, 69–131.Google Scholar
[Pi] Pierce, R. S., Associative Algebras. Graduate Texts Math. 88, Springer-Verlag, New York, 1982.Google Scholar
[Sh] Shelstad, D., Notes on L-indistinguishability (based on a lecture by R. P. Langlands). In: Automorphic forms, representations and L-functions. American Mathematical Society, Providence, RI, 1979, pp. 193–203.Google Scholar
[We] Weil, A., Basic Number Theory. Grundlehren der Mathematischen Wissenschaften 144, Springer-Verlag, New York, 1973.Google Scholar