Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-10T15:15:50.674Z Has data issue: false hasContentIssue false
  • English
  • Français

Shortest paths in arbitrary plane domains

Part of: Special properties Real and complex geometry

Published online by Cambridge University Press:  09 November 2020

L. C. Hoehn ,
L. G. Oversteegen  and
E. D. Tymchatyn
L. C. Hoehn
Affiliation:
Department of Computer Science & Mathematics, Nipissing University, 100 College Drive, Box 5002, North Bay, ON P1B 8L7, Canada e-mail: loganh@nipissingu.ca
L. G. Oversteegen*
Affiliation:
Department of Mathematics, University of Alabama at Birmingham, Birmingham, AL 35294, USA
E. D. Tymchatyn
Affiliation:
Department of Mathematics and Statistics, University of Saskatchewan, 106 Wiggins Road, Saskatoon, SK S7N 5E6, Canada e-mail: tymchat@math.usask.ca
*
e-mail: overstee@uab.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\Omega $ be a connected open set in the plane and $\gamma : [0,1] \to \overline {\Omega }$ a path such that $\gamma ((0,1)) \subset \Omega $ . We show that the path 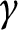$\gamma $ can be “pulled tight” to a unique shortest path which is homotopic to 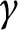$\gamma $ , via a homotopy h with endpoints fixed whose intermediate paths $h_t$ , for 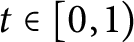$t \in [0,1)$ , satisfy 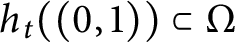$h_t((0,1)) \subset \Omega $ . We prove this result even in the case when there is no path of finite Euclidean length homotopic to 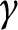$\gamma $ under such a homotopy. For this purpose, we offer three other natural, equivalent notions of a “shortest” path. This work generalizes previous results for simply connected domains with simple closed curve boundaries.

Keywords

Pathlengthshortestplane domainhomotopyanalytic covering map

MSC classification

Primary: 54F50: Spaces of dimension $leq 1$; curves, dendrites
Secondary: 51M25: Length, area and volume
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 349 - 367
Check for updates
Copyright
© Canadian Mathematical Society 2020

Footnotes

L.C.H. was partially supported by NSERC grant RGPIN 435518. L.G.O. was partially supported by NSF-DMS-1807558. E.D.T. was partially supported by NSERC grant OGP-0005616.

References

Ahlfors, L. V., Conformal invariants: topics in geometric function theory. McGraw-Hill Series in Higher Mathematics, McGraw-Hill Book Co., New York, Düsseldorf, Johannesburg, 1973. MR 0357743.Google Scholar
Bourgin, R. D. and Renz, P. L., Shortest paths in simply connected regions in R2 . Adv. Math. 76(1989), no. 2, 260–295. MR 1013673.CrossRefGoogle Scholar
Cannon, J. W., Conner, G. R., and Zastrow, A., One-dimensional sets and planar sets are aspherical . Topol. Appl. 120(2002), nos. 1–2, 23–45. In memory of T. Benny Rushing. MR 1895481.CrossRefGoogle Scholar
Conway, J. B., Functions of one complex variable. II . Graduate Texts in Mathematics, 159, Springer-Verlag, New York, NY, 1995. MR 1344449.Google Scholar
Fatou, P., Séries trigonométriques et séries de Taylor . Acta Math. 30(1906), no. 1, 335–400. MR 1555035.CrossRefGoogle Scholar
Hoehn, L. C., Oversteegen, L. G., and Tymchatyn, E. D., Extension of isotopies in the plane . Trans. Amer. Math. Soc. 372(2019), no. 7, 4889–4915. MR 4009398.CrossRefGoogle Scholar
Hoehn, L. C., Oversteegen, L. G., and Tymchatyn, E. D., A canonical parameterization of paths in ℝ n . Houston J. Math. 46(2020), 465–489.Google Scholar
Kent, C., Homotopy type of planar continua. Preprint, 2020, arXiv:1709.09211 CrossRefGoogle Scholar
Kuratowski, K., Topology, Vol. II . New ed., revised and augmented. Translated from the French by A. Kirkor. Academic Press, New York, NY, 1968.Google Scholar
Lindelöf, E., Sur un principe générale de l’analyse et ses applications à la théorie de la représentation conforme . Acta Soc. Sci. Fennicae 46(1915), 1–35.Google Scholar
Morse, M., A special parameterization of curves . Bull. Amer. Math. Soc. 42(1936), no. 12, 915–922. MR 1563464.CrossRefGoogle Scholar
Pommerenke, C., Boundary behaviour of conformal maps . Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 299, Springer-Verlag, Berlin, Germany, 1992. MR 1217706.Google Scholar
Riesz, F., Über die Randwerte einer analytischen Funktion . Math. Z. 18(1923), no. 1, 87–95. MR 1544621.CrossRefGoogle Scholar
Riesz, F. and Riesz, M., Über die Randwerte einer analytischen Function 4. Cong. Scand. Math. Stockholm 1916, pp. 87–95.Google Scholar
Silverman, E., Equicontinuity and n-length . Proc. Amer. Math. Soc. 20(1969), 483–486. MR 0237719 (38 #6000).Google Scholar