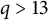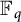1 Introduction
Throughout the paper, let p be an odd prime and q a power of p. Let
![]() $\mathbb {F}_q$
be the finite field with q elements. Let
$\mathbb {F}_q$
be the finite field with q elements. Let
![]() $d \mid (q-1)$
such that
$d \mid (q-1)$
such that
![]() $d>1$
. We denote
$d>1$
. We denote
![]() $S_d(\mathbb {F}_q)=\{x^d: x \in \mathbb {F}_q^*\}$
to be the subgroup of
$S_d(\mathbb {F}_q)=\{x^d: x \in \mathbb {F}_q^*\}$
to be the subgroup of
![]() $\mathbb {F}_q^*$
with order
$\mathbb {F}_q^*$
with order
![]() $\frac {q-1}{d}$
. If q is assumed to be fixed, for brevity, we simply write
$\frac {q-1}{d}$
. If q is assumed to be fixed, for brevity, we simply write
![]() $S_d$
instead of
$S_d$
instead of
![]() $S_d(\mathbb {F}_q)$
.
$S_d(\mathbb {F}_q)$
.
A celebrated conjecture of Sárközy [Reference Sárközy25] asserts that if p is a sufficiently large prime, then
![]() $S_2$
does not admit a nontrivial additive decomposition, that is,
$S_2$
does not admit a nontrivial additive decomposition, that is,
![]() $S_2$
cannot be written as
$S_2$
cannot be written as
![]() $S_2=A+B$
, where
$S_2=A+B$
, where
![]() $A, B \subset \mathbb {F}_p$
and
$A, B \subset \mathbb {F}_p$
and
![]() $|A|, |B| \geq 2$
. Recall that the sumset
$|A|, |B| \geq 2$
. Recall that the sumset
![]() $A+B$
is defined to be
$A+B$
is defined to be
![]() $A+B=\{a+b: a \in A, b \in B\}$
. This conjecture is still widely open. Recently, Hanson and Petridis [Reference Hanson and Petridis16] made important progress on this conjecture: they showed that Sárközy’s conjecture holds for almost all primes. More generally, one can study the additive decomposition problem for any multiplicative subgroup of a finite field; see, for example, [Reference Hanson and Petridis16, Reference Shkredov28–Reference Shparlinski30, Reference Yip37].
$A+B=\{a+b: a \in A, b \in B\}$
. This conjecture is still widely open. Recently, Hanson and Petridis [Reference Hanson and Petridis16] made important progress on this conjecture: they showed that Sárközy’s conjecture holds for almost all primes. More generally, one can study the additive decomposition problem for any multiplicative subgroup of a finite field; see, for example, [Reference Hanson and Petridis16, Reference Shkredov28–Reference Shparlinski30, Reference Yip37].
We establish the restricted sumset analog of Sárközy’s conjecture below, namely that the set of nonzero squares in a finite field does not admit a restricted sumset decomposition. Recall that for a given set A, its restricted sumset is given by
![]() $A \hat {+} A=\{a+b: a,b \in A, a \neq b\}$
.
$A \hat {+} A=\{a+b: a,b \in A, a \neq b\}$
.
Theorem 1.1 If
![]() $q>13$
is an odd prime power, then the set of nonzero squares in
$q>13$
is an odd prime power, then the set of nonzero squares in
![]() $\mathbb {F}_q$
cannot be written as a restricted sumset of a set. In other words,
$\mathbb {F}_q$
cannot be written as a restricted sumset of a set. In other words,
![]() $S_2 \neq A\hat {+}A$
for any
$S_2 \neq A\hat {+}A$
for any
![]() $A \subset \mathbb {F}_q$
.
$A \subset \mathbb {F}_q$
.
As one of the fundamental objects, restricted sumsets appear frequently in the study of additive number theory and additive combinatorics. For example, they appear in the celebrated Erdős–Heilbronn conjecture (an analog of Cauchy–Devanport theorem for restricted sumsets), first confirmed by Dias da Silva and Hamidoune [Reference Dias da Silva and Hamidoune8] (see also [Reference Alon, Nathanson and Ruzsa1] for a different proof by Alon, Nathanson, and Ruzsa). They also naturally appear in a question of Erdős [Reference Erdős9] and Moser [Reference Sierpiński31] (independently) related to perfect squares, as well as the study of cliques in Cayley sum graphs [Reference Green13, Reference Green and Morris14]. In particular, we will also discuss some implications of our results on these two types of problems.
Our main motivation for establishing Theorem 1.1 is to extend a result due to Shkredov [Reference Shkredov27], where he showed that if
![]() $p>13$
is a prime, then
$p>13$
is a prime, then
![]() $S_2 \subset \mathbb {F}_p$
cannot be written as
$S_2 \subset \mathbb {F}_p$
cannot be written as
![]() $A \hat {+}A$
. His proof is very delicateFootnote
1
: it is based on Fourier analytic methods and it also uses some results from the theory of perfect difference sets. HeFootnote
2
remarked that it is challenging to extend his proof over a general finite field with prime power order, mainly due to a corresponding result in the theory of perfect difference sets seems to be absent. He also remarked that his proof cannot be extended to study the same problem for multiplicative subgroups with index at least
$A \hat {+}A$
. His proof is very delicateFootnote
1
: it is based on Fourier analytic methods and it also uses some results from the theory of perfect difference sets. HeFootnote
2
remarked that it is challenging to extend his proof over a general finite field with prime power order, mainly due to a corresponding result in the theory of perfect difference sets seems to be absent. He also remarked that his proof cannot be extended to study the same problem for multiplicative subgroups with index at least
![]() $3$
(that is,
$3$
(that is,
![]() $S_d$
with
$S_d$
with
![]() $d \geq 3$
). Indeed, our proof of Theorem 1.1 is completely different from his proof. Moreover, our techniques can be used to handle general multiplicative subgroups with some additional assumptions. In particular, we prove the following result, which is of a probabilistic flavor.
$d \geq 3$
). Indeed, our proof of Theorem 1.1 is completely different from his proof. Moreover, our techniques can be used to handle general multiplicative subgroups with some additional assumptions. In particular, we prove the following result, which is of a probabilistic flavor.
Theorem 1.2 Let s be a positive integer and
![]() $d \geq 3$
. If s is even, further assume that d is not twice a perfect square. Among the set of primes
$d \geq 3$
. If s is even, further assume that d is not twice a perfect square. Among the set of primes
![]() $p \equiv 1\ \pmod d$
, the lower asymptotic density of primes p such that there is no
$p \equiv 1\ \pmod d$
, the lower asymptotic density of primes p such that there is no
![]() $A \subset \mathbb {F}_{p^{s}}$
with
$A \subset \mathbb {F}_{p^{s}}$
with
![]() $A\hat {+}A=S_d(\mathbb {F}_{p^{s}})$
is at least
$A\hat {+}A=S_d(\mathbb {F}_{p^{s}})$
is at least
![]() $1-\frac {(d-1)^r}{4d^r}$
, where
$1-\frac {(d-1)^r}{4d^r}$
, where
![]() $r=\lceil s/2 \rceil -1$
.
$r=\lceil s/2 \rceil -1$
.
In particular, when
![]() $s=1$
(which corresponds to prime fields), the above lower asymptotic density is at least
$s=1$
(which corresponds to prime fields), the above lower asymptotic density is at least
![]() $\frac {3}{4}$
. Also observe that as
$\frac {3}{4}$
. Also observe that as
![]() $s \to \infty $
, the above lower asymptotic density tends to
$s \to \infty $
, the above lower asymptotic density tends to
![]() $1$
. When s is even and d is twice a perfect square, the following theorem supplements Theorem 1.2.
$1$
. When s is even and d is twice a perfect square, the following theorem supplements Theorem 1.2.
Theorem 1.3 Let
![]() $k \geq 3$
be a positive integer and let
$k \geq 3$
be a positive integer and let
![]() $d=2k^2$
. If q is an even power of a prime
$d=2k^2$
. If q is an even power of a prime
![]() $p \equiv 1\ \pmod d$
, then
$p \equiv 1\ \pmod d$
, then
![]() $A \hat {+} A \neq S_d$
for any
$A \hat {+} A \neq S_d$
for any
![]() $A \subset \mathbb {F}_q$
.
$A \subset \mathbb {F}_q$
.
To prove the above results, one key ingredient we develop is the following theorem. Roughly speaking, if
![]() $A\hat {+}A=S_d$
, then A is “very close to” being a Sidon set.
$A\hat {+}A=S_d$
, then A is “very close to” being a Sidon set.
Theorem 1.4 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $p \equiv 1\ \pmod d$
be a prime. Let q be a power of p such that
$p \equiv 1\ \pmod d$
be a prime. Let q be a power of p such that
![]() $\frac {q-1}{d} \geq 3$
. Assume that there is
$\frac {q-1}{d} \geq 3$
. Assume that there is
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A\hat {+}A=S_d$
. If
$A\hat {+}A=S_d$
. If
![]() $|A|$
is odd or
$|A|$
is odd or
![]() $0 \in A$
, then A is a Sidon set with
$0 \in A$
, then A is a Sidon set with
![]() $\{2a: a \in A\} \cap S_d=\emptyset $
, and
$\{2a: a \in A\} \cap S_d=\emptyset $
, and
If
![]() $|A|$
is even, then
$|A|$
is even, then
 $$ \begin{align*}|A|=2\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil, \quad \text{and} \quad \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
$$ \begin{align*}|A|=2\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil, \quad \text{and} \quad \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
Recall
![]() $A=\{a_1, a_2, \ldots , a_N\} \subset \mathbb {F}_q$
is a Sidon set if all pairwise sums
$A=\{a_1, a_2, \ldots , a_N\} \subset \mathbb {F}_q$
is a Sidon set if all pairwise sums
![]() $a_i+a_j$
(for
$a_i+a_j$
(for
![]() $i \leq j$
) are different. Theorem 1.4 is partially inspired by an interesting connection between Sárközy’s conjecture and co-Sidon sets described in the recent work of Hanson and Petridis [Reference Hanson and Petridis16] (see also a related work by Lev and Sonn [Reference Lev and Sonn20]). It is straightforward to use Theorem 1.4 to deduce Theorem 1.3. Theorem 1.4 also implies the following corollary.
$i \leq j$
) are different. Theorem 1.4 is partially inspired by an interesting connection between Sárközy’s conjecture and co-Sidon sets described in the recent work of Hanson and Petridis [Reference Hanson and Petridis16] (see also a related work by Lev and Sonn [Reference Lev and Sonn20]). It is straightforward to use Theorem 1.4 to deduce Theorem 1.3. Theorem 1.4 also implies the following corollary.
Corollary 1.5 Let
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $k \geq 3$
. If k is even, additionally assume that
$k \geq 3$
. If k is even, additionally assume that
![]() $d \neq 8$
. Then there exists
$d \neq 8$
. Then there exists
![]() $p_0=p_0(d,k)$
, such that if
$p_0=p_0(d,k)$
, such that if
![]() $p>p_0$
is a prime such that
$p>p_0$
is a prime such that
![]() $p \equiv 1 \ \pmod d$
and
$p \equiv 1 \ \pmod d$
and
![]() $A \subset \mathbb {F}_{p^k}$
such that
$A \subset \mathbb {F}_{p^k}$
such that
![]() $A\hat {+}A=S_d(\mathbb {F}_{p^k})$
, then
$A\hat {+}A=S_d(\mathbb {F}_{p^k})$
, then
![]() $|A|$
is even and
$|A|$
is even and
![]() $0 \not \in A$
.
$0 \not \in A$
.
Next, we discuss upper bounds on
![]() $|A|$
assuming
$|A|$
assuming
![]() $A \hat {+} A \subset S_d \cup \{0\}$
. Using a standard double character sum estimate, one can show that
$A \hat {+} A \subset S_d \cup \{0\}$
. Using a standard double character sum estimate, one can show that
![]() $|A|< \sqrt {q}+3$
(see Lemma 2.4). When
$|A|< \sqrt {q}+3$
(see Lemma 2.4). When
![]() $q=p$
is a prime, we show that this square root upper bound can be improved to roughly
$q=p$
is a prime, we show that this square root upper bound can be improved to roughly
![]() $\sqrt {2q/d}$
, which provides a multiplicative factor
$\sqrt {2q/d}$
, which provides a multiplicative factor
![]() $\sqrt {2/d}$
improvement.
$\sqrt {2/d}$
improvement.
Theorem 1.6 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $p \equiv 1 \ \pmod d$
be a prime. Assume that
$p \equiv 1 \ \pmod d$
be a prime. Assume that
![]() $A \subset \mathbb {F}_p$
. If
$A \subset \mathbb {F}_p$
. If
![]() $A \hat {+} A \subset S_d$
, then
$A \hat {+} A \subset S_d$
, then
![]() $|A|\leq \sqrt {2(p-1)/d+1}+1$
; if
$|A|\leq \sqrt {2(p-1)/d+1}+1$
; if
![]() $A \hat {+} A \subset S_d \cup \{0\}$
, then
$A \hat {+} A \subset S_d \cup \{0\}$
, then
![]() $|A|\leq \sqrt {2(p-1)/d+1}+2$
.
$|A|\leq \sqrt {2(p-1)/d+1}+2$
.
When q is square and
![]() $d \geq 3$
, we show that this upper bound from character sum estimates can be improved to
$d \geq 3$
, we show that this upper bound from character sum estimates can be improved to
![]() $\sqrt {q}$
below. Moreover, this is in general best possible since the
$\sqrt {q}$
below. Moreover, this is in general best possible since the
![]() $\sqrt {q}$
bound can be achieved by an infinite family.
$\sqrt {q}$
bound can be achieved by an infinite family.
Theorem 1.7 Let
![]() $d \geq 3$
. Let
$d \geq 3$
. Let
![]() $q \equiv 1 \ \pmod d$
be an odd prime power and a square. If
$q \equiv 1 \ \pmod d$
be an odd prime power and a square. If
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A\hat {+}A \subset S_d \cup \{0\}$
, then
$A\hat {+}A \subset S_d \cup \{0\}$
, then
![]() $|A| \leq \sqrt {q}$
, with the equality holds if and only if
$|A| \leq \sqrt {q}$
, with the equality holds if and only if
![]() $d \mid (\sqrt {q}+1)$
and
$d \mid (\sqrt {q}+1)$
and
![]() $A=\alpha \mathbb {F}_{\sqrt {q}}$
, where
$A=\alpha \mathbb {F}_{\sqrt {q}}$
, where
![]() $\alpha \in S_d$
.
$\alpha \in S_d$
.
A well-known conjecture due to van Lint and MacWilliams [Reference van Lint and MacWilliams34] states that if q is an odd prime power and a square, and A is a subset of
![]() $\mathbb {F}_{q}$
such that
$\mathbb {F}_{q}$
such that
![]() $0,1 \in A$
,
$0,1 \in A$
,
![]() $|A|=\sqrt {q}$
, and
$|A|=\sqrt {q}$
, and
![]() $A-A \subset S_2 \cup \{0\}$
, then A must be given by the subfield
$A-A \subset S_2 \cup \{0\}$
, then A must be given by the subfield
![]() $\mathbb {F}_{\sqrt {q}}$
. The conjecture was first proved by Blokhuis [Reference Blokhuis4], and its various generalizations were confirmed in [Reference Asgarli and Yip2, Reference Sziklai33, Reference Yip36]. Thus, Theorem 1.7 establishes an analog of van Lint–MacWilliams’ conjecture for restricted sumsets. Theorems 1.6 and 1.7 can be also formulated in terms of clique number and maximum cliques in the corresponding Cayley sum graphs; we refer to Section 3.2 for more discussions. We also refer to Remark 3.6 on a connection between Theorem 1.7 and the celebrated Erdős--Ko--Rado Theorem [Reference Erdős, Ko and Rado10].
$\mathbb {F}_{\sqrt {q}}$
. The conjecture was first proved by Blokhuis [Reference Blokhuis4], and its various generalizations were confirmed in [Reference Asgarli and Yip2, Reference Sziklai33, Reference Yip36]. Thus, Theorem 1.7 establishes an analog of van Lint–MacWilliams’ conjecture for restricted sumsets. Theorems 1.6 and 1.7 can be also formulated in terms of clique number and maximum cliques in the corresponding Cayley sum graphs; we refer to Section 3.2 for more discussions. We also refer to Remark 3.6 on a connection between Theorem 1.7 and the celebrated Erdős--Ko--Rado Theorem [Reference Erdős, Ko and Rado10].
Finally, we discuss the implications of our results to a related problem over integers. Erdős [Reference Erdős9] and Moser [Reference Sierpiński31] independently asked whether for all k there are integers
![]() $a_1<\ldots <a_k$
such that
$a_1<\ldots <a_k$
such that
![]() $a_i+a_j$
is a perfect square for all
$a_i+a_j$
is a perfect square for all
![]() $1 \leq i <j \leq k$
. It is easy to verify that the uniformity conjecture [Reference Caporaso, Harris and Mazur6] implies that the answer to their question is negative (see the related discussion in [Reference Shkredov and Solymosi26, Section 5]). Lagrange [Reference Lagrange19] and Nicolas [Reference Nicolas23] found a set of
$1 \leq i <j \leq k$
. It is easy to verify that the uniformity conjecture [Reference Caporaso, Harris and Mazur6] implies that the answer to their question is negative (see the related discussion in [Reference Shkredov and Solymosi26, Section 5]). Lagrange [Reference Lagrange19] and Nicolas [Reference Nicolas23] found a set of
![]() $6$
integers such that the sum of any two of them is a perfect square (see also a recent paper of Choudhry [Reference Choudhry7]), and it is unknown whether there is a set of
$6$
integers such that the sum of any two of them is a perfect square (see also a recent paper of Choudhry [Reference Choudhry7]), and it is unknown whether there is a set of
![]() $7$
integers satisfying such property.
$7$
integers satisfying such property.
In the other direction, Rivat, Sárközy, and Stewart [Reference Rivat, Sárközy and Stewart24, Theorem 6] proved that if
![]() $A \subset \{1, \ldots , N\}$
and
$A \subset \{1, \ldots , N\}$
and
![]() $A \hat {+} A$
is contained in the set of perfect squares, then
$A \hat {+} A$
is contained in the set of perfect squares, then
![]() $|A|\leq (36+o(1))\log N$
. Gyarmati [Reference Gyarmati15, Theorem 9] considered a generalization of the problem by Erdős and Moser, and proved that if
$|A|\leq (36+o(1))\log N$
. Gyarmati [Reference Gyarmati15, Theorem 9] considered a generalization of the problem by Erdős and Moser, and proved that if
![]() $d \geq 2$
is fixed, and
$d \geq 2$
is fixed, and
![]() $A,B \subset \{1,2,\ldots , N\}$
such that
$A,B \subset \{1,2,\ldots , N\}$
such that
![]() $A+B$
is contained in the set of perfect d-th powers, then
$A+B$
is contained in the set of perfect d-th powers, then
![]() $\min (|A|, |B|)\leq (4d+o(1)) \log N$
. In particular, her result implies that the upper bound in the result of Rivat, Sárközy, and Stewart can be improved from
$\min (|A|, |B|)\leq (4d+o(1)) \log N$
. In particular, her result implies that the upper bound in the result of Rivat, Sárközy, and Stewart can be improved from
![]() $(36+o(1))\log N$
to
$(36+o(1))\log N$
to
![]() $(16+o(1))\log N$
. We further improve their upper bound to
$(16+o(1))\log N$
. We further improve their upper bound to
![]() $(1+o(1))\log N$
, as a special case of the following more general result:
$(1+o(1))\log N$
, as a special case of the following more general result:
Theorem 1.8 Let
![]() $d \geq 2$
. If
$d \geq 2$
. If
![]() $A\subset \{1,2,\ldots , N\}$
such that
$A\subset \{1,2,\ldots , N\}$
such that
![]() $A \hat {+} A$
is contained in the set of perfect d-th powers, then as
$A \hat {+} A$
is contained in the set of perfect d-th powers, then as
![]() $N \to \infty $
, we have
$N \to \infty $
, we have
1.1 Structure of the paper
In Section 2, we provide extra background on the topic. In Section 3, we estimate
![]() $|A|$
assuming
$|A|$
assuming
![]() $A\hat {+}A \subset S_d$
. In particular, we prove Theorems 1.6 and 1.7. The goal of Section 4 is to investigate the possibility of decomposing a multiplicative subgroup as a restricted sumset. In particular, we prove Theorems 1.1, 1.2, and 1.3. To achieve that, we need to first establish Theorem 1.4 on the connection between this problem with Sidon sets. Finally, in Section 5, we discuss the applications of our main results to the question of Erdős and Moser and its variant, and we prove Theorem 1.8.
$A\hat {+}A \subset S_d$
. In particular, we prove Theorems 1.6 and 1.7. The goal of Section 4 is to investigate the possibility of decomposing a multiplicative subgroup as a restricted sumset. In particular, we prove Theorems 1.1, 1.2, and 1.3. To achieve that, we need to first establish Theorem 1.4 on the connection between this problem with Sidon sets. Finally, in Section 5, we discuss the applications of our main results to the question of Erdős and Moser and its variant, and we prove Theorem 1.8.
2 Background
2.1 Hyper-derivatives
Our proof is based on Stepanov’s method, inspired by [Reference Hanson and Petridis16, Reference Stepanov32, Reference Yip37].
We recall a few basic properties of hyper-derivatives (also known as Hasse derivatives); we refer to a general discussion in [Reference Lidl and Niederreiter21, Section 6.4].
Definition 2.1 Let
![]() $c_0,c_1, \ldots c_d \in \mathbb {F}_q$
. If n is a non-negative integer, then the n-th hyper-derivative of
$c_0,c_1, \ldots c_d \in \mathbb {F}_q$
. If n is a non-negative integer, then the n-th hyper-derivative of
![]() $f(x)=\sum _{j=0}^d c_j x^j$
is
$f(x)=\sum _{j=0}^d c_j x^j$
is
 $$ \begin{align*}E^{(n)}(f) =\sum_{j=0}^d \binom{j}{n} c_j x^{j-n}, \end{align*} $$
$$ \begin{align*}E^{(n)}(f) =\sum_{j=0}^d \binom{j}{n} c_j x^{j-n}, \end{align*} $$
where we follow the standard convention that
![]() $\binom {j}{n}=0$
for
$\binom {j}{n}=0$
for
![]() $j<n$
, so that the n-th hyper-derivative is a polynomial.
$j<n$
, so that the n-th hyper-derivative is a polynomial.
Lemma 2.1 [Reference Lidl and Niederreiter21, Corollary 6.48]
Let
![]() $n,d$
be positive integers. If
$n,d$
be positive integers. If
![]() $c \in \mathbb {F}_q$
, then
$c \in \mathbb {F}_q$
, then
![]() $E^{(n)}\big ((x+c)^d\big )=\binom {d}{n} (x+c)^{d-n}.$
$E^{(n)}\big ((x+c)^d\big )=\binom {d}{n} (x+c)^{d-n}.$
Lemma 2.2 [Reference Lidl and Niederreiter21, Lemma 6.51]
Let f be a nonzero polynomial in
![]() $\mathbb {F}_q[x]$
. If c is a root of
$\mathbb {F}_q[x]$
. If c is a root of
![]() $E^{(n)}(f)$
for
$E^{(n)}(f)$
for
![]() $n=0,1,\ldots , m-1$
, then c is a root of multiplicity at least m.
$n=0,1,\ldots , m-1$
, then c is a root of multiplicity at least m.
Lemma 2.3 (Leibniz rule for hyper-derivatives, [Reference Lidl and Niederreiter21, Lemma 6.47])
If
![]() $f, g \in \mathbb {F}_q[x]$
, then
$f, g \in \mathbb {F}_q[x]$
, then
 $$ \begin{align*}E^{(n)}(fg)= \sum_{k=0}^n E^{(k)} (f) E^{(n-k)} (g). \end{align*} $$
$$ \begin{align*}E^{(n)}(fg)= \sum_{k=0}^n E^{(k)} (f) E^{(n-k)} (g). \end{align*} $$
2.2 Square-root upper bound
Lemma 2.4 Let
![]() $A \subset \mathbb {F}_q$
. If
$A \subset \mathbb {F}_q$
. If
![]() $A+A \subset S_d \cup \{0\}$
, then
$A+A \subset S_d \cup \{0\}$
, then
![]() $|A|\leq \sqrt {q}$
, with equality holding only if q is a square and
$|A|\leq \sqrt {q}$
, with equality holding only if q is a square and
![]() $A=-A$
. If
$A=-A$
. If
![]() $A\hat {+}A \subset S_d \cup \{0\}$
, then
$A\hat {+}A \subset S_d \cup \{0\}$
, then
![]() $|A|< \sqrt {q}+3$
.
$|A|< \sqrt {q}+3$
.
Proof Let
![]() $\chi $
be a multiplicative character of
$\chi $
be a multiplicative character of
![]() $\mathbb {F}_q$
with order d. We have the following double character sum estimate (see, for example, [Reference Yip36, Theorem 2.6]):
$\mathbb {F}_q$
with order d. We have the following double character sum estimate (see, for example, [Reference Yip36, Theorem 2.6]):
 $$ \begin{align} \bigg|\sum_{a,b\in A}\chi(a+b)\bigg| \leq \sqrt{q}|A|\bigg(1-\frac{|A|}{q}\bigg). \end{align} $$
$$ \begin{align} \bigg|\sum_{a,b\in A}\chi(a+b)\bigg| \leq \sqrt{q}|A|\bigg(1-\frac{|A|}{q}\bigg). \end{align} $$
We first assume that
![]() $A+A \subset S_d \cup \{0\}$
. Note that for each
$A+A \subset S_d \cup \{0\}$
. Note that for each
![]() $a \in A$
, we have
$a \in A$
, we have
![]() $a+b \in S_d$
for each
$a+b \in S_d$
for each
![]() $b \in A$
, unless
$b \in A$
, unless
![]() $a+b=0$
. It follows that
$a+b=0$
. It follows that
and the equality holds if and only if
![]() $A=-A$
. Combining inequality (2.1) and inequality (2.2), we have
$A=-A$
. Combining inequality (2.1) and inequality (2.2), we have
 $$ \begin{align*}|A|^2-|A| \leq \sqrt{q}|A|\bigg(1-\frac{|A|}{q}\bigg). \end{align*} $$
$$ \begin{align*}|A|^2-|A| \leq \sqrt{q}|A|\bigg(1-\frac{|A|}{q}\bigg). \end{align*} $$
It follows that
![]() $|A|\leq \sqrt {q}$
, and the equality holds only if
$|A|\leq \sqrt {q}$
, and the equality holds only if
![]() $A=-A$
.
$A=-A$
.
Next, we work under the weaker assumption that
![]() $A\hat {+}A \subset S_d \cup \{0\}$
. The proof is essentially the same, and the only difference is
$A\hat {+}A \subset S_d \cup \{0\}$
. The proof is essentially the same, and the only difference is
![]() $\chi (2a)$
could be anything. We instead have
$\chi (2a)$
could be anything. We instead have
 $$ \begin{align*}|A|^2-3|A| \leq \bigg|\sum_{a,b\in A}\chi(a+b)\bigg|\leq \sqrt{q}|A|\bigg(1-\frac{|A|}{q}\bigg)<\sqrt{q}|A|, \end{align*} $$
$$ \begin{align*}|A|^2-3|A| \leq \bigg|\sum_{a,b\in A}\chi(a+b)\bigg|\leq \sqrt{q}|A|\bigg(1-\frac{|A|}{q}\bigg)<\sqrt{q}|A|, \end{align*} $$
which implies that
![]() $|A|<\sqrt {q}+3$
.
$|A|<\sqrt {q}+3$
.
2.3 Sumsets in multiplicative subgroups
The following theorem is an extension of [Reference Hanson and Petridis16, Theorem 1.2], which is the main result in [Reference Hanson and Petridis16] by Hanson and Petridis, to all finite fields, with an extra assumption on the non-vanishing of a binomial coefficient. Its proof is based on Stepanov’s method.
Theorem 2.5 [Reference Yip37, Theorem 1.1]
Let
![]() $d \mid (q-1)$
such that
$d \mid (q-1)$
such that
![]() $d>1$
. If
$d>1$
. If
![]() $A,B \subset \mathbb {F}_q$
such that
$A,B \subset \mathbb {F}_q$
such that
![]() $A+B\subset S_d \cup \{0\}$
and
$A+B\subset S_d \cup \{0\}$
and
![]() $ \binom {|B|-1+\frac {q-1}{d}}{\frac {q-1}{d}}\not \equiv 0 \ \pmod p,$
then
$ \binom {|B|-1+\frac {q-1}{d}}{\frac {q-1}{d}}\not \equiv 0 \ \pmod p,$
then
As remarked in [Reference Yip37], in general, the condition on the binomial coefficient cannot be dropped. On the other hand, when q is a prime, it is easy to verify that the condition on the binomial coefficient always holds, and thus Theorem 1.1 recovers [Reference Hanson and Petridis16, Theorem 1.2]. Theorem 2.5 can be used to make progress on Sárközy’s conjecture and its generalization; see [Reference Hanson and Petridis16, Reference Yip37].
We remark that Theorem 2.5 can already be used to deduce non-trivial results on restricted sumsets. For example, it is straightforward to apply Theorem 2.5 to show the following: if
![]() $A \subset \mathbb {F}_p$
and
$A \subset \mathbb {F}_p$
and
![]() $A \hat {+} A \subset S_d$
, then
$A \hat {+} A \subset S_d$
, then
![]() $|A|\leq 2\sqrt {p/d}+O(1)$
; indeed, we can write A as the disjoint union of two sets B and C such that
$|A|\leq 2\sqrt {p/d}+O(1)$
; indeed, we can write A as the disjoint union of two sets B and C such that
![]() $|B|$
and
$|B|$
and
![]() $|C|$
differ by
$|C|$
differ by
![]() $1$
, and then
$1$
, and then
![]() $B+C \subset A \hat {+} A \subset S_d$
. However, such “naive” applications of Theorem 2.5 are not strong enough for our applications to restricted sumset decompositions. Furthermore, under the same setting, Theorem 1.6 provides a bound of the form
$B+C \subset A \hat {+} A \subset S_d$
. However, such “naive” applications of Theorem 2.5 are not strong enough for our applications to restricted sumset decompositions. Furthermore, under the same setting, Theorem 1.6 provides a bound of the form
![]() $\sqrt {2p/d}+O(1)$
, which is much better. For our applications, we still require Theorem 2.5, but we will use it in a rather indirect way. Moreover, we also need to establish an analog of Theorem 2.5 that is particularly designed for restricted sumsets, which we discuss next.
$\sqrt {2p/d}+O(1)$
, which is much better. For our applications, we still require Theorem 2.5, but we will use it in a rather indirect way. Moreover, we also need to establish an analog of Theorem 2.5 that is particularly designed for restricted sumsets, which we discuss next.
3 Upper bounds on
 $|A|$
assuming
$|A|$
assuming
 $A\hat {+}A \subset S_d$
$A\hat {+}A \subset S_d$
In this section, our main aim is to give an upper bound on
![]() $|A|$
provided that
$|A|$
provided that
![]() $A\hat {+}A \subset S_d$
. Note that if
$A\hat {+}A \subset S_d$
. Note that if
![]() $A+A \subset S_d \cup \{0\}$
, then we can use Theorem 2.5 to give an upper bound on
$A+A \subset S_d \cup \{0\}$
, then we can use Theorem 2.5 to give an upper bound on
![]() $|A|$
. Thus we can further assume that
$|A|$
. Thus we can further assume that
![]() $A+A \not \subset S_d \cup \{0\}$
, and indeed we will take advantage of this additional assumption in a crucial way in the following proofs. Since the restricted subset
$A+A \not \subset S_d \cup \{0\}$
, and indeed we will take advantage of this additional assumption in a crucial way in the following proofs. Since the restricted subset
![]() $A \hat {+} A$
is generally much more difficult to analyze compared to the sumset
$A \hat {+} A$
is generally much more difficult to analyze compared to the sumset
![]() $A+A$
, when we apply Stepanov’s method in this setting, the arguments we present will be more delicate compared to those used to study sumsets [Reference Hanson and Petridis16, Reference Yip37].
$A+A$
, when we apply Stepanov’s method in this setting, the arguments we present will be more delicate compared to those used to study sumsets [Reference Hanson and Petridis16, Reference Yip37].
3.1 Applications of Stepanov’s method
The following proposition may be viewed as an analog of Theorem 2.5 in the restricted sumset setting.
Proposition 3.1 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod d$
be an odd prime power. Let
$q \equiv 1 \ \pmod d$
be an odd prime power. Let
![]() $A \subset \mathbb {F}_q$
with
$A \subset \mathbb {F}_q$
with
![]() $|A|=N$
such that
$|A|=N$
such that
![]() $A\hat {+}A \subset S_d$
while
$A\hat {+}A \subset S_d$
while
![]() $A+A \not \subset S_d \cup \{0\}$
.
$A+A \not \subset S_d \cup \{0\}$
.
-
(1) If N is odd, then
 $$ \begin{align*}\frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d \cup \{0\}\} \leq \frac{q-1}{d}. \end{align*} $$
$$ \begin{align*}\frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d \cup \{0\}\} \leq \frac{q-1}{d}. \end{align*} $$
-
(2) If N is even, then
 $$ \begin{align*}\frac{(N-1)^2+1}{2} \leq \frac{q-1}{d}. \end{align*} $$
$$ \begin{align*}\frac{(N-1)^2+1}{2} \leq \frac{q-1}{d}. \end{align*} $$
Moreover, further assume that
 $0 \in A$
, then we have the stronger estimate
$0 \in A$
, then we have the stronger estimate  $$ \begin{align*}\frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d\} \leq \frac{q-1}{d}.\end{align*} $$
$$ \begin{align*}\frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d\} \leq \frac{q-1}{d}.\end{align*} $$
Proof Let
![]() $A=\{a_1,a_2,\ldots , a_N\}$
. If
$A=\{a_1,a_2,\ldots , a_N\}$
. If
![]() $N=1$
, the statements are trivially true. Next, assume
$N=1$
, the statements are trivially true. Next, assume
![]() $N \geq 2$
. If
$N \geq 2$
. If
![]() $0 \in A$
, without loss of generality we assume that
$0 \in A$
, without loss of generality we assume that
![]() $a_N=0$
. Let
$a_N=0$
. Let
![]() $n=N$
if n is odd, and let
$n=N$
if n is odd, and let
![]() $n=N-1$
if n is even. Let
$n=N-1$
if n is even. Let
![]() $m=(n-1)/2$
; then
$m=(n-1)/2$
; then
![]() $m \geq 1$
.
$m \geq 1$
.
Since
![]() $A \hat {+} A \subset S_d$
, we have
$A \hat {+} A \subset S_d$
, we have
for each
![]() $1 \leq i,j \leq N$
(note that when
$1 \leq i,j \leq N$
(note that when
![]() $i=j$
, both sides are equal to
$i=j$
, both sides are equal to
![]() $0$
). This simple observation will be used repeatedly in the following computation.
$0$
). This simple observation will be used repeatedly in the following computation.
The Vandermonde matrix
is invertible. Let
![]() $c_1,c_2,...,c_n$
be the unique solution of the following system of equations:
$c_1,c_2,...,c_n$
be the unique solution of the following system of equations:
 $$ \begin{align} \left\{ \begin{array}{ll} \sum_{i=1}^n c_i a_i^j=0, &\quad 0 \leq j \leq 2m-1=n-2\\ \\ \sum_{i=1}^n c_i a_i^{n-1}=1.\end{array}\right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} \sum_{i=1}^n c_i a_i^j=0, &\quad 0 \leq j \leq 2m-1=n-2\\ \\ \sum_{i=1}^n c_i a_i^{n-1}=1.\end{array}\right. \end{align} $$
We note that
![]() $c_i \neq 0$
for each
$c_i \neq 0$
for each
![]() $1 \leq i \leq n$
; otherwise we must have
$1 \leq i \leq n$
; otherwise we must have
![]() $c_1=c_2=\ldots =c_n=0$
in view of the first
$c_1=c_2=\ldots =c_n=0$
in view of the first
![]() $n-1$
equations in system (3.2), which contradicts the last equation in system (3.2).
$n-1$
equations in system (3.2), which contradicts the last equation in system (3.2).
Consider the following auxiliary polynomial
 $$ \begin{align} f(x)=-(-1)^m+\sum_{i=1}^n c_i (x+a_i)^{m+\frac{q-1}{d}} (x-a_i)^{m}\in \mathbb{F}_q[x]. \end{align} $$
$$ \begin{align} f(x)=-(-1)^m+\sum_{i=1}^n c_i (x+a_i)^{m+\frac{q-1}{d}} (x-a_i)^{m}\in \mathbb{F}_q[x]. \end{align} $$
First, observe that the degree of f is at most
![]() $\frac {q-1}{d}$
. Indeed, for each
$\frac {q-1}{d}$
. Indeed, for each
![]() $0 \leq j \leq 2m-1$
, the coefficient of
$0 \leq j \leq 2m-1$
, the coefficient of
![]() $x^{2m+\frac {q-1}{d}-j}$
in
$x^{2m+\frac {q-1}{d}-j}$
in
![]() $f(x)$
is
$f(x)$
is
 $$ \begin{align*} &\sum_{i=1}^n \sum_{k=0}^j \bigg(\binom{m+\frac{q-1}{d}}{k} c_i a_i^{k} \cdot \binom{m}{j-k} (-a_i)^{j-k}\bigg)\\ &\quad =\sum_{k=0}^j \binom{m+\frac{q-1}{d}}{k} \binom{m}{j-k} \cdot \bigg(\sum_{i=1}^n c_i a_i^{k} (-a_i)^{j-k}\bigg)\\ &\quad =\bigg(\sum_{i=1}^n c_i a_i^{j} \bigg) \cdot \bigg(\sum_{k=0}^j \binom{m+\frac{q-1}{d}}{k} \binom{m}{j-k} (-1)^{j-k}\bigg)=0 \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^n \sum_{k=0}^j \bigg(\binom{m+\frac{q-1}{d}}{k} c_i a_i^{k} \cdot \binom{m}{j-k} (-a_i)^{j-k}\bigg)\\ &\quad =\sum_{k=0}^j \binom{m+\frac{q-1}{d}}{k} \binom{m}{j-k} \cdot \bigg(\sum_{i=1}^n c_i a_i^{k} (-a_i)^{j-k}\bigg)\\ &\quad =\bigg(\sum_{i=1}^n c_i a_i^{j} \bigg) \cdot \bigg(\sum_{k=0}^j \binom{m+\frac{q-1}{d}}{k} \binom{m}{j-k} (-1)^{j-k}\bigg)=0 \end{align*} $$
by the assumption in system (3.2).
For each
![]() $1\leq j \leq N$
, Equation (3.1) and system (3.2) imply that
$1\leq j \leq N$
, Equation (3.1) and system (3.2) imply that
 $$ \begin{align*} E^{(0)} f (a_j) = f (a_j) &= -(-1)^m+\sum_{i=1}^n c_i (a_j+a_i)^{m+\frac{q-1}{d}} (a_j-a_i)^{m} \\ &= -(-1)^m+\sum_{i=1}^n c_i (a_j+a_i)^{m} (a_j-a_i)^{m}\\ &= -(-1)^m+\sum_{i=1}^n c_i (a_j^2-a_i^2)^{m} \\ &= -(-1)^m+ \sum_{\ell=0}^m \binom{m}{\ell} a_j^{2(m-\ell)} (-1)^\ell\bigg(\sum_{i=1}^n c_i a_i^{2\ell}\bigg) \\ &= -(-1)^m+ (-1)^m \bigg(\sum_{i=1}^n c_i a_i^{n-1}\bigg) =0. \end{align*} $$
$$ \begin{align*} E^{(0)} f (a_j) = f (a_j) &= -(-1)^m+\sum_{i=1}^n c_i (a_j+a_i)^{m+\frac{q-1}{d}} (a_j-a_i)^{m} \\ &= -(-1)^m+\sum_{i=1}^n c_i (a_j+a_i)^{m} (a_j-a_i)^{m}\\ &= -(-1)^m+\sum_{i=1}^n c_i (a_j^2-a_i^2)^{m} \\ &= -(-1)^m+ \sum_{\ell=0}^m \binom{m}{\ell} a_j^{2(m-\ell)} (-1)^\ell\bigg(\sum_{i=1}^n c_i a_i^{2\ell}\bigg) \\ &= -(-1)^m+ (-1)^m \bigg(\sum_{i=1}^n c_i a_i^{n-1}\bigg) =0. \end{align*} $$
Next, we compute the hyper-derivatives of f on A. We first prove the following claim: for each
![]() $1 \leq j \leq N$
, if
$1 \leq j \leq N$
, if
![]() $0 \leq k_1\leq m$
and
$0 \leq k_1\leq m$
and
![]() $0\leq k_2<m$
such that
$0\leq k_2<m$
such that
![]() $1\leq k_1+k_2 \leq m$
, then we have
$1\leq k_1+k_2 \leq m$
, then we have
 $$ \begin{align} \sum_{i=1}^n c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^m](a_j)=0. \end{align} $$
$$ \begin{align} \sum_{i=1}^n c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^m](a_j)=0. \end{align} $$
Indeed, by Lemma 2.1 and Equation (3.1), we have
 $$ \begin{align*} &\sum_{i=1}^n c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^m](a_j)\\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \bigg(\sum_{i=1}^n c_i (a_j+a_i)^{m-k_1+\frac{q-1}{d}} (a_j-a_i)^{m-k_2}\bigg) \\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \bigg(\sum_{i=1}^n c_i (a_j+a_i)^{m-k_1} (a_j-a_i)^{m-k_2}\bigg) \\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \cdot\sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2} \bigg(\sum_{i=1}^n c_i a_j^{m-k_1-\ell_1} a_i^{\ell_1} a_j^{m-k_2-\ell_2}(-a_i)^{\ell_2}\bigg)\\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \cdot\sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2}\\ &\quad \times a_j^{(m-k_1-\ell_1)+(m-k_2-\ell_2)} (-1)^{\ell_2}\bigg(\sum_{i=1}^n c_i a_i^{\ell_1+\ell_2} \bigg)\\ &=0, \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^n c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^m](a_j)\\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \bigg(\sum_{i=1}^n c_i (a_j+a_i)^{m-k_1+\frac{q-1}{d}} (a_j-a_i)^{m-k_2}\bigg) \\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \bigg(\sum_{i=1}^n c_i (a_j+a_i)^{m-k_1} (a_j-a_i)^{m-k_2}\bigg) \\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \cdot\sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2} \bigg(\sum_{i=1}^n c_i a_j^{m-k_1-\ell_1} a_i^{\ell_1} a_j^{m-k_2-\ell_2}(-a_i)^{\ell_2}\bigg)\\ &= \binom{m+\frac{q-1}{d}}{k_1} \binom{m}{k_2} \cdot\sum_{\ell_1=0}^{m-k_1} \sum_{\ell_2=0}^{m-k_2} \binom{m-k_1}{\ell_1} \binom{m-k_2}{\ell_2}\\ &\quad \times a_j^{(m-k_1-\ell_1)+(m-k_2-\ell_2)} (-1)^{\ell_2}\bigg(\sum_{i=1}^n c_i a_i^{\ell_1+\ell_2} \bigg)\\ &=0, \end{align*} $$
where we again use the assumptions in system (3.2), since we always have
![]() $\ell _1+\ell _2\leq 2m-k_1-k_2 \leq 2m-1$
for the exponent in the last summand.
$\ell _1+\ell _2\leq 2m-k_1-k_2 \leq 2m-1$
for the exponent in the last summand.
From the above claim (3.4) and Lemma 2.3, it follows that for each
![]() $1\leq j \leq N$
and
$1\leq j \leq N$
and
![]() $1 \leq r \leq m-1$
, we have
$1 \leq r \leq m-1$
, we have
 $$ \begin{align*} E^{(r)} f (a_j) = \sum_{i=1}^n c_i \bigg(\sum_{k=0}^r E^{(k)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(r-k)}[(x-a_i)^{m}](a_j)\bigg) =0. \end{align*} $$
$$ \begin{align*} E^{(r)} f (a_j) = \sum_{i=1}^n c_i \bigg(\sum_{k=0}^r E^{(k)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(r-k)}[(x-a_i)^{m}](a_j)\bigg) =0. \end{align*} $$
Similarly, for each
![]() $1 \leq j \leq N$
, we have
$1 \leq j \leq N$
, we have
 $$ \begin{align} E^{(m)} f (a_j) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(k)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(m-k)}[(x-a_i)^{m}](a_j)\bigg) \notag \\ &= \sum_{i=1}^n c_i E^{(0)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(m)}[(x-a_i)^{m}](a_j) \notag\\ &= \sum_{i=1}^n c_i (a_j+a_i)^{m+\frac{q-1}{d}}. \end{align} $$
$$ \begin{align} E^{(m)} f (a_j) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(k)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(m-k)}[(x-a_i)^{m}](a_j)\bigg) \notag \\ &= \sum_{i=1}^n c_i E^{(0)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(m)}[(x-a_i)^{m}](a_j) \notag\\ &= \sum_{i=1}^n c_i (a_j+a_i)^{m+\frac{q-1}{d}}. \end{align} $$
Recall that if
![]() $j \neq i$
, then
$j \neq i$
, then
![]() $a_j+a_i \in S_d$
and thus
$a_j+a_i \in S_d$
and thus
![]() $(a_j+a_i)^{\frac {q-1}{d}}=1$
. If
$(a_j+a_i)^{\frac {q-1}{d}}=1$
. If
![]() $1 \leq j \leq n$
, then Equation (3.5) further simplifies to
$1 \leq j \leq n$
, then Equation (3.5) further simplifies to
 $$ \begin{align} E^{(m)} f (a_j) &= c_j (2a_j)^{m+\frac{q-1}{d}}+\sum_{\substack{1\leq i \leq n \\i \neq j}} c_i (a_j+a_i)^{m} \notag\\ &= c_j (2a_j)^{m+\frac{q-1}{d}} -c_j (2a_j)^m +\sum_{i=1}^n c_i (a_j+a_i)^{m} \notag\\ &= c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg)+\sum_{k=0}^m \binom{m}{k} a_j^{m-k} \bigg(\sum_{i=1}^n c_i a_i^k\bigg) \notag\\ &=c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg). \end{align} $$
$$ \begin{align} E^{(m)} f (a_j) &= c_j (2a_j)^{m+\frac{q-1}{d}}+\sum_{\substack{1\leq i \leq n \\i \neq j}} c_i (a_j+a_i)^{m} \notag\\ &= c_j (2a_j)^{m+\frac{q-1}{d}} -c_j (2a_j)^m +\sum_{i=1}^n c_i (a_j+a_i)^{m} \notag\\ &= c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg)+\sum_{k=0}^m \binom{m}{k} a_j^{m-k} \bigg(\sum_{i=1}^n c_i a_i^k\bigg) \notag\\ &=c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg). \end{align} $$
Note that if
![]() $2a_j=0$
, that is,
$2a_j=0$
, that is,
![]() $a_j=0$
, then
$a_j=0$
, then
![]() $E^{(m)} f (a_j)=0$
. If
$E^{(m)} f (a_j)=0$
. If
![]() $2a_j \in S_d$
, then
$2a_j \in S_d$
, then
![]() $(2a_j)^{\frac {q-1}{d}}=1$
and we also have
$(2a_j)^{\frac {q-1}{d}}=1$
and we also have
![]() $E^{(m)} f (a_j)=0$
. Conversely, if
$E^{(m)} f (a_j)=0$
. Conversely, if
![]() $E^{(m)} f (a_j)=0$
, then we must also have
$E^{(m)} f (a_j)=0$
, then we must also have
![]() $2a_j \in S_d \cup \{0\}$
since
$2a_j \in S_d \cup \{0\}$
since
![]() $c_j \neq 0$
. Thus,
$c_j \neq 0$
. Thus,
![]() $E^{(m)} f (a_j)=0$
if and only if
$E^{(m)} f (a_j)=0$
if and only if
![]() $2a_j \in S_d \cup \{0\}$
. Since
$2a_j \in S_d \cup \{0\}$
. Since
![]() $A +A \not \subset S_d \cup \{0\}$
, there is
$A +A \not \subset S_d \cup \{0\}$
, there is
![]() $1\leq j_0\leq n$
such that
$1\leq j_0\leq n$
such that
![]() $2a_{j_0} \not \in S_d \cup \{0\}$
, and thus
$2a_{j_0} \not \in S_d \cup \{0\}$
, and thus
![]() $E^{(m)} f (a_{j_0})\neq 0$
, which implies that f is not identically
$E^{(m)} f (a_{j_0})\neq 0$
, which implies that f is not identically
![]() $0$
.
$0$
.
In view of Lemma 2.2, for each
![]() $1 \leq j \leq n$
, we have shown that
$1 \leq j \leq n$
, we have shown that
![]() $a_j$
is a root of f with multiplicity at least m; moreover, if additionally
$a_j$
is a root of f with multiplicity at least m; moreover, if additionally
![]() $2a_j \in S_d \cup \{0\}$
, then
$2a_j \in S_d \cup \{0\}$
, then
![]() $a_j$
is a root with multiplicity at least
$a_j$
is a root with multiplicity at least
![]() $m+1$
. To complete the proof, we consider the parity of N.
$m+1$
. To complete the proof, we consider the parity of N.
(1) N is odd. In this case,
![]() $n=N$
and
$n=N$
and
![]() $m=\frac {N-1}{2}$
. We conclude that
$m=\frac {N-1}{2}$
. We conclude that
 $$ \begin{align*} & \frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d \cup \{0\}\} \\ &\quad =mN+\#\{1 \leq j \leq N: 2a_j \in S_d \cup \{0\}\} \leq \deg f \leq \frac{q-1}{d}. \end{align*} $$
$$ \begin{align*} & \frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d \cup \{0\}\} \\ &\quad =mN+\#\{1 \leq j \leq N: 2a_j \in S_d \cup \{0\}\} \leq \deg f \leq \frac{q-1}{d}. \end{align*} $$
(2) N is even. In this case,
![]() $n=N-1$
. Note that
$n=N-1$
. Note that
![]() $a_i+a_N \in S_d$
for each
$a_i+a_N \in S_d$
for each
![]() $1 \leq i \leq n$
, and thus Equation (3.5) and system (3.2) imply that
$1 \leq i \leq n$
, and thus Equation (3.5) and system (3.2) imply that
 $$ \begin{align*} E^{(m)} f (a_N)= \sum_{i=1}^n c_i (a_N+a_i)^{m+\frac{q-1}{d}}= \sum_{i=1}^n c_i (a_N+a_i)^{m}=\sum_{k=0}^m \binom{m}{k} a_N^{m-k} \bigg(\sum_{i=1}^n c_ia_i^k\bigg)=0. \end{align*} $$
$$ \begin{align*} E^{(m)} f (a_N)= \sum_{i=1}^n c_i (a_N+a_i)^{m+\frac{q-1}{d}}= \sum_{i=1}^n c_i (a_N+a_i)^{m}=\sum_{k=0}^m \binom{m}{k} a_N^{m-k} \bigg(\sum_{i=1}^n c_ia_i^k\bigg)=0. \end{align*} $$
Thus,
![]() $a_j$
is a root of f with multiplicity at least m for each
$a_j$
is a root of f with multiplicity at least m for each
![]() $1 \leq j \leq n$
, and
$1 \leq j \leq n$
, and
![]() $a_N$
is in fact a root of f with multiplicity at least
$a_N$
is in fact a root of f with multiplicity at least
![]() $m+1$
. It follows that
$m+1$
. It follows that
Finally, we additionally assume that
![]() $0 \in A$
, that is,
$0 \in A$
, that is,
![]() $a_N=0$
. Then we must have
$a_N=0$
. Then we must have
![]() $a_i \in S_d$
and thus
$a_i \in S_d$
and thus
![]() $a_i^{\frac {q-1}{d}}=1$
for each
$a_i^{\frac {q-1}{d}}=1$
for each
![]() $1 \leq i \leq n$
. A similar computation shows that
$1 \leq i \leq n$
. A similar computation shows that
 $$ \begin{align*} E^{(r)} f (0) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(r-k)}[(x+a_i)^{m+\frac{q-1}{d}}](0) \cdot E^{(k)}[(x-a_i)^{m}](0)\bigg)\\ &= \sum_{k=0}^m \binom{m+\frac{q-1}{d}}{r-k} \binom{m}{k} \bigg(\sum_{i=1}^n c_i a_i^{m-r+k+\frac{q-1}{d}} (-a_i)^{m-k}\bigg)\\ &= \sum_{k=0}^m \binom{m+\frac{q-1}{d}}{r-k} \binom{m}{k} (-1)^{m-k}\bigg(\sum_{i=1}^n c_i a_i^{2m-r+\frac{q-1}{d}}\bigg)\\ &= \sum_{k=0}^m \binom{m+\frac{q-1}{d}}{r-k} \binom{m}{k} (-1)^{m-k}\bigg(\sum_{i=1}^n c_i a_i^{2m-r}\bigg)=0 \end{align*} $$
$$ \begin{align*} E^{(r)} f (0) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(r-k)}[(x+a_i)^{m+\frac{q-1}{d}}](0) \cdot E^{(k)}[(x-a_i)^{m}](0)\bigg)\\ &= \sum_{k=0}^m \binom{m+\frac{q-1}{d}}{r-k} \binom{m}{k} \bigg(\sum_{i=1}^n c_i a_i^{m-r+k+\frac{q-1}{d}} (-a_i)^{m-k}\bigg)\\ &= \sum_{k=0}^m \binom{m+\frac{q-1}{d}}{r-k} \binom{m}{k} (-1)^{m-k}\bigg(\sum_{i=1}^n c_i a_i^{2m-r+\frac{q-1}{d}}\bigg)\\ &= \sum_{k=0}^m \binom{m+\frac{q-1}{d}}{r-k} \binom{m}{k} (-1)^{m-k}\bigg(\sum_{i=1}^n c_i a_i^{2m-r}\bigg)=0 \end{align*} $$
for each
![]() $m+1 \leq r \leq 2m$
. Thus, in this case,
$m+1 \leq r \leq 2m$
. Thus, in this case,
![]() $0=a_N$
is in fact a root of f with multiplicity at least
$0=a_N$
is in fact a root of f with multiplicity at least
![]() $2m+1=n=N-1$
. Consequently, we have a stronger bound that
$2m+1=n=N-1$
. Consequently, we have a stronger bound that
 $$ \begin{align*} &\frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d\}\\ &\quad =(N-1) \cdot \frac{(N-2)}{2}+ \#\{1\leq j \leq n: 2a \in S_d\}+(N-1)\leq \deg f \leq \frac{q-1}{d}. \end{align*} $$
$$ \begin{align*} &\frac{N(N-1)}{2}+\#\{a \in A: 2a \in S_d\}\\ &\quad =(N-1) \cdot \frac{(N-2)}{2}+ \#\{1\leq j \leq n: 2a \in S_d\}+(N-1)\leq \deg f \leq \frac{q-1}{d}. \end{align*} $$
In view of Theorems 1.6 and 1.7, we also need to consider the case that
![]() $A\hat {+}A \subset S_d \cup \{0\}$
. Next, we prove that a slightly weaker bound still holds under this weaker assumption.
$A\hat {+}A \subset S_d \cup \{0\}$
. Next, we prove that a slightly weaker bound still holds under this weaker assumption.
Proposition 3.2 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod d$
be an odd prime power. Let
$q \equiv 1 \ \pmod d$
be an odd prime power. Let
![]() $A' \subset \mathbb {F}_q$
such that
$A' \subset \mathbb {F}_q$
such that
![]() $A'\hat {+}A' \subset S_d \cup \{0\}$
while
$A'\hat {+}A' \subset S_d \cup \{0\}$
while
![]() $A'+A' \not \subset S_d \cup \{0\}$
. Then
$A'+A' \not \subset S_d \cup \{0\}$
. Then
![]() $|A'|\leq \sqrt {2(q-1)/d+1}+2$
.
$|A'|\leq \sqrt {2(q-1)/d+1}+2$
.
Proof Since
![]() $A'\hat {+}A' \subset S_d \cup \{0\}$
and
$A'\hat {+}A' \subset S_d \cup \{0\}$
and
![]() $A'+A' \not \subset S_d \cup \{0\}$
, there is
$A'+A' \not \subset S_d \cup \{0\}$
, there is
![]() $a^* \in A'$
such that
$a^* \in A'$
such that
![]() $2a^* \not \subset S_d \cup \{0\}$
. Note that
$2a^* \not \subset S_d \cup \{0\}$
. Note that
![]() $a^* \neq 0$
and thus
$a^* \neq 0$
and thus
![]() $-a^* \neq a^*$
. Let
$-a^* \neq a^*$
. Let
![]() $A=A' \setminus \{-a^*\}$
. Then
$A=A' \setminus \{-a^*\}$
. Then
![]() $|A|=|A'|$
or
$|A|=|A'|$
or
![]() $|A|=|A'|-1$
. Thus, it suffices to show
$|A|=|A'|-1$
. Thus, it suffices to show
![]() $|A|\leq \sqrt {2(q-1)/d+1}+1$
.
$|A|\leq \sqrt {2(q-1)/d+1}+1$
.
Let
![]() $A=\{a_1,a_2, \ldots , a_N\}$
. We can assume that
$A=\{a_1,a_2, \ldots , a_N\}$
. We can assume that
![]() $|A|\geq 2$
. Without loss of generality, we may assume that
$|A|\geq 2$
. Without loss of generality, we may assume that
![]() $a_1=a^*$
. The proof is essentially the same as the proof of Proposition 3.1. We use the same notations and use the same polynomial. While Equation (3.1) may fail, we instead have
$a_1=a^*$
. The proof is essentially the same as the proof of Proposition 3.1. We use the same notations and use the same polynomial. While Equation (3.1) may fail, we instead have
for each
![]() $1 \leq i, j \leq N$
. Almost identical arguments lead to the following information on f:
$1 \leq i, j \leq N$
. Almost identical arguments lead to the following information on f:
-
•
 $\deg f \leq \frac {q-1}{d}$
.
$\deg f \leq \frac {q-1}{d}$
. -
•
 $f(a_j)=0$
for each
$f(a_j)=0$
for each
 $1 \leq j \leq N$
.
$1 \leq j \leq N$
. -
• A slightly weaker claim, namely
(3.7)holds for each $$ \begin{align} \sum_{i=1}^N c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^{m}](a_j)=0. \end{align} $$
$$ \begin{align} \sum_{i=1}^N c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^{m}](a_j)=0. \end{align} $$
 $1 \leq j \leq N$
, provided that
$1 \leq j \leq N$
, provided that
 $0 \leq k_1,k_2<m$
and
$0 \leq k_1,k_2<m$
and
 $1 \leq k_1+k_2 \leq m$
. Compared to the claim in the proof of Proposition 3.1, we also need to deal with the cases
$1 \leq k_1+k_2 \leq m$
. Compared to the claim in the proof of Proposition 3.1, we also need to deal with the cases
 $k_1=m$
and
$k_1=m$
and
 $k_2=0$
separately.
$k_2=0$
separately.
-
• Lemma 2.3 then allows us to deduce that
 $E^{(r)} f (a_j)=0$
for
$E^{(r)} f (a_j)=0$
for
 $1\leq j \leq N$
and
$1\leq j \leq N$
and
 $0 \leq r \leq m-1$
.
$0 \leq r \leq m-1$
.
Since
![]() $-a_1=-a^* \notin A$
, it follows that
$-a_1=-a^* \notin A$
, it follows that
![]() $a_i+a_1 \neq 0$
for each
$a_i+a_1 \neq 0$
for each
![]() $1 \leq i \leq N$
, so that we have
$1 \leq i \leq N$
, so that we have
Thus, following a similar computation as in the deduction of Equations (3.5) and (3.6) in the proof of Proposition 3.1, we have
 $$ \begin{align*} E^{(m)} f (a_1) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(k)}[(x+a_i)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m-k)}[(x-a_i)^{m}](a_1)\bigg) \\ &= \sum_{i=1}^n c_i E^{(0)}[(x+a_i)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m)}[(x-a_i)^{m}](a_1)\\ &\quad +\sum_{i=1}^n c_i E^{(m)}[(x+a_i)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(0)}[(x-a_i)^{m}](a_1)\\ &= \sum_{i=1}^n c_i (a_1+a_i)^{m+\frac{q-1}{d}} +\binom{m+\frac{q-1}{d}}{m} \sum_{i=1}^{n} c_i (a_1+a_i)^{\frac{q-1}{d}}(a_1-a_i)^m\\ &= \sum_{i=1}^n c_i (a_1+a_i)^{m+\frac{q-1}{d}} +\binom{m+\frac{q-1}{d}}{m} \sum_{i=1}^{n} c_i (a_1-a_i)^m\\ &= c_1 (2a_1)^m \bigg((2a_1)^{\frac{q-1}{d}}-1\bigg) \neq 0 \end{align*} $$
$$ \begin{align*} E^{(m)} f (a_1) &= \sum_{i=1}^n c_i \bigg(\sum_{k=0}^m E^{(k)}[(x+a_i)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m-k)}[(x-a_i)^{m}](a_1)\bigg) \\ &= \sum_{i=1}^n c_i E^{(0)}[(x+a_i)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(m)}[(x-a_i)^{m}](a_1)\\ &\quad +\sum_{i=1}^n c_i E^{(m)}[(x+a_i)^{m+\frac{q-1}{d}}](a_1) \cdot E^{(0)}[(x-a_i)^{m}](a_1)\\ &= \sum_{i=1}^n c_i (a_1+a_i)^{m+\frac{q-1}{d}} +\binom{m+\frac{q-1}{d}}{m} \sum_{i=1}^{n} c_i (a_1+a_i)^{\frac{q-1}{d}}(a_1-a_i)^m\\ &= \sum_{i=1}^n c_i (a_1+a_i)^{m+\frac{q-1}{d}} +\binom{m+\frac{q-1}{d}}{m} \sum_{i=1}^{n} c_i (a_1-a_i)^m\\ &= c_1 (2a_1)^m \bigg((2a_1)^{\frac{q-1}{d}}-1\bigg) \neq 0 \end{align*} $$
since
![]() $2a_1 \not \in S_d \cup \{0\}$
. In particular, f is not identically zero. Therefore, Lemma 2.2 implies that
$2a_1 \not \in S_d \cup \{0\}$
. In particular, f is not identically zero. Therefore, Lemma 2.2 implies that
It follows that
![]() $N \leq \sqrt {2(q-1)/d+1}+1$
and the proof is complete.
$N \leq \sqrt {2(q-1)/d+1}+1$
and the proof is complete.
3.2 Proof of Theorems 1.6 and 1.7, and their implications to Cayley sum graphs
We first deduce Theorem 1.6.
Proof of Theorem 1.6
If
![]() $A+A \subset S_d \cup \{0\}$
, then Theorem 2.5 implies that
$A+A \subset S_d \cup \{0\}$
, then Theorem 2.5 implies that
![]() $|A|^2 \leq \frac {p-1}{d}+|A|$
, so
$|A|^2 \leq \frac {p-1}{d}+|A|$
, so
![]() $|A|\leq \sqrt {p/d}+1$
. Next assume that
$|A|\leq \sqrt {p/d}+1$
. Next assume that
![]() $A +A \not \subset S_d \cup \{0\}$
. Then the upper bound on
$A +A \not \subset S_d \cup \{0\}$
. Then the upper bound on
![]() $|A|$
follows from Propositions 3.1 and 3.2.
$|A|$
follows from Propositions 3.1 and 3.2.
Before proving Theorem 1.7, we recall a few basic terminologies from graph theory. A clique in a graph X is a subset of vertices in which every two distinct vertices are adjacent, and the clique number of X, denoted
![]() $\omega (X)$
, is the size of a maximum clique. The graphs related to our discussions are the widely studied generalized Paley graphs.
$\omega (X)$
, is the size of a maximum clique. The graphs related to our discussions are the widely studied generalized Paley graphs.
We follow the notations in [Reference Asgarli and Yip2, Reference Yip36]. Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod {2d}$
be a prime power. The d-Paley graph over
$q \equiv 1 \ \pmod {2d}$
be a prime power. The d-Paley graph over
![]() $\mathbb {F}_q$
, denoted
$\mathbb {F}_q$
, denoted
![]() $GP(q,d)$
, is the graph whose vertices are the elements of
$GP(q,d)$
, is the graph whose vertices are the elements of
![]() $\mathbb {F}_q$
, where two vertices are adjacent if and only if the difference of the two vertices is a d-th power in
$\mathbb {F}_q$
, where two vertices are adjacent if and only if the difference of the two vertices is a d-th power in
![]() $\mathbb {F}_q^*$
. The condition
$\mathbb {F}_q^*$
. The condition
![]() $q \equiv 1 \ \pmod {2d}$
guarantees that
$q \equiv 1 \ \pmod {2d}$
guarantees that
![]() $GP(q,d)$
is undirected and non-degenerate (see for example [Reference Yip36, p. 1]). Now we are ready to prove Theorem 1.7 with the help of existing results on d-Paley graphs.
$GP(q,d)$
is undirected and non-degenerate (see for example [Reference Yip36, p. 1]). Now we are ready to prove Theorem 1.7 with the help of existing results on d-Paley graphs.
Proof of Theorem 1.7
When
![]() $q \leq 121$
, we have checked the theorem by SageMath. Next, assume that
$q \leq 121$
, we have checked the theorem by SageMath. Next, assume that
![]() $q>121$
. Let
$q>121$
. Let
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A \hat {+} A \subset S_d \cup \{0\}$
.
$A \hat {+} A \subset S_d \cup \{0\}$
.
If
![]() $A+A \not \subset S_d \cup \{0\}$
, then Proposition 3.2 implies that
$A+A \not \subset S_d \cup \{0\}$
, then Proposition 3.2 implies that
![]() $|A|\leq \sqrt {\frac {2(q-1)}{d}+1}+2$
. Note that when
$|A|\leq \sqrt {\frac {2(q-1)}{d}+1}+2$
. Note that when
![]() $q>121$
, we have
$q>121$
, we have
 $$ \begin{align*}|A| \leq \sqrt{\frac{2(q-1)}{d}+1}+2 \leq \sqrt{\frac{2(q-1)}{3}+1}+2<\sqrt{q} \end{align*} $$
$$ \begin{align*}|A| \leq \sqrt{\frac{2(q-1)}{d}+1}+2 \leq \sqrt{\frac{2(q-1)}{3}+1}+2<\sqrt{q} \end{align*} $$
since
![]() $d \geq 3$
. Next we consider the case that
$d \geq 3$
. Next we consider the case that
![]() $A+A \subset S_d \cup \{0\}$
. By Lemma 2.4,
$A+A \subset S_d \cup \{0\}$
. By Lemma 2.4,
![]() $|A|\leq \sqrt {q}$
, with equality holding only if
$|A|\leq \sqrt {q}$
, with equality holding only if
![]() $A=-A$
. Thus, we have proved the first assertion that
$A=-A$
. Thus, we have proved the first assertion that
![]() $|A|\leq \sqrt {q}$
.
$|A|\leq \sqrt {q}$
.
It remains to characterize A such that
![]() $|A|=\sqrt {q}$
and
$|A|=\sqrt {q}$
and
![]() $A+A \subset S_d \cup \{0\}$
. The above analysis shows that we must have
$A+A \subset S_d \cup \{0\}$
. The above analysis shows that we must have
![]() $A=-A$
and
$A=-A$
and
![]() $0 \in A$
(since q is odd). Thus
$0 \in A$
(since q is odd). Thus
![]() $A-A=A+A \subset S_d \cup \{0\}$
. Since
$A-A=A+A \subset S_d \cup \{0\}$
. Since
![]() $A-A=-(A-A)$
, we must have
$A-A=-(A-A)$
, we must have
![]() $-1 \in S_d$
. Since
$-1 \in S_d$
. Since
![]() $q \equiv 1 \ \pmod d$
, this implies that
$q \equiv 1 \ \pmod d$
, this implies that
![]() $q \equiv 1 \ \pmod {2d}$
, so that the d-Paley graph over
$q \equiv 1 \ \pmod {2d}$
, so that the d-Paley graph over
![]() $\mathbb {F}_q$
, is well-defined. Using this terminology, A is a clique in
$\mathbb {F}_q$
, is well-defined. Using this terminology, A is a clique in
![]() $GP(q,d)$
with size
$GP(q,d)$
with size
![]() $\sqrt {q}$
. It then follows from [Reference Yip36, Theorem 1.2] that
$\sqrt {q}$
. It then follows from [Reference Yip36, Theorem 1.2] that
![]() $d \mid (\sqrt {q}+1)$
. Note that the condition
$d \mid (\sqrt {q}+1)$
. Note that the condition
![]() $d \mid (\sqrt {q}+1)$
implies that
$d \mid (\sqrt {q}+1)$
implies that
![]() $\mathbb {F}_{\sqrt {q}}^* \subset S_d$
. Moreover, Sziklai [Reference Sziklai33] showed that if
$\mathbb {F}_{\sqrt {q}}^* \subset S_d$
. Moreover, Sziklai [Reference Sziklai33] showed that if
![]() $0,1 \in A$
, then
$0,1 \in A$
, then
![]() $A=\mathbb {F}_{\sqrt {q}}$
; see also [Reference Yip36, Theorem 2.9] and [Reference Asgarli and Yip2, Section 2]. Note that
$A=\mathbb {F}_{\sqrt {q}}$
; see also [Reference Yip36, Theorem 2.9] and [Reference Asgarli and Yip2, Section 2]. Note that
![]() $0 \in A$
while
$0 \in A$
while
![]() $1$
is not necessarily in A, so we conclude that
$1$
is not necessarily in A, so we conclude that
![]() $A=\alpha \mathbb {F}_{\sqrt {q}}$
for some
$A=\alpha \mathbb {F}_{\sqrt {q}}$
for some
![]() $\alpha \in S_d$
. Conversely, it it easy to verify that, if
$\alpha \in S_d$
. Conversely, it it easy to verify that, if
![]() $\alpha \in S_d$
, then
$\alpha \in S_d$
, then
![]() $\alpha \mathbb {F}_{\sqrt {q}} \hat {+} \alpha \mathbb {F}_{\sqrt {q}}=\alpha \mathbb {F}_{\sqrt {q}} \subset S_d \cup \{0\}$
. This completes the proof of the theorem.
$\alpha \mathbb {F}_{\sqrt {q}} \hat {+} \alpha \mathbb {F}_{\sqrt {q}}=\alpha \mathbb {F}_{\sqrt {q}} \subset S_d \cup \{0\}$
. This completes the proof of the theorem.
Remark 3.3 Our analysis cannot handle the case
![]() $d=2$
. In fact, there is
$d=2$
. In fact, there is
![]() $A \subset \mathbb {F}_9$
with size
$A \subset \mathbb {F}_9$
with size
![]() $4$
such that
$4$
such that
![]() $A \hat {+} A \subset S_2 (\mathbb {F}_9) \cup \{0\}$
, and there are
$A \hat {+} A \subset S_2 (\mathbb {F}_9) \cup \{0\}$
, and there are
![]() $15$
different
$15$
different
![]() $A \subset \mathbb {F}_{25}$
with size
$A \subset \mathbb {F}_{25}$
with size
![]() $5$
such that
$5$
such that
![]() $A \hat {+} A \subset S_2 (\mathbb {F}_{25}) \cup \{0\}$
. Nevertheless, we conjecture that when q is an odd square and
$A \hat {+} A \subset S_2 (\mathbb {F}_{25}) \cup \{0\}$
. Nevertheless, we conjecture that when q is an odd square and
![]() $q \geq 49$
, the statement of Theorem 1.7 also extends to the case
$q \geq 49$
, the statement of Theorem 1.7 also extends to the case
![]() $d=2$
.
$d=2$
.
We have seen the connection between our results and cliques in generalized Paley graphs from the above proof. Next, we further explore such a connection and reformulate our results using the language of graphs. We need to recall the notions of Cayley graphs and Cayley sum graphs.
Let G be an abelian group and let
![]() $D \subset G$
. The Cayley graph
$D \subset G$
. The Cayley graph
![]() $\operatorname {Cay}(G, D)$
(typically one needs to further assume that
$\operatorname {Cay}(G, D)$
(typically one needs to further assume that
![]() $0 \not \in D$
and
$0 \not \in D$
and
![]() $D=-D$
) is the undirected graph whose vertices are elements of G, such that two vertices g and h are adjacent if and only if
$D=-D$
) is the undirected graph whose vertices are elements of G, such that two vertices g and h are adjacent if and only if
![]() $g-h \in D$
. One can similarly define Cayley sum graphs: the Cayley sum graph
$g-h \in D$
. One can similarly define Cayley sum graphs: the Cayley sum graph
![]() $\operatorname {CayS}(G, D)$
is the undirected graph whose vertices are elements of G, such that two (distinct) vertices g and h are adjacent if and only if
$\operatorname {CayS}(G, D)$
is the undirected graph whose vertices are elements of G, such that two (distinct) vertices g and h are adjacent if and only if
![]() $g+h \in D$
. In particular, note that a subset A of vertices is a clique in a Cayley sum
$g+h \in D$
. In particular, note that a subset A of vertices is a clique in a Cayley sum
![]() $X=\operatorname {CayS}(G, D)$
if and only if
$X=\operatorname {CayS}(G, D)$
if and only if
![]() $A\hat {+} A \subset D$
, thus cliques in X are closely connected to restricted sumsets.
$A\hat {+} A \subset D$
, thus cliques in X are closely connected to restricted sumsets.
Let
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $q \equiv 1 \ \pmod d$
be an odd prime power. We define the d-Paley sum graph over
$q \equiv 1 \ \pmod d$
be an odd prime power. We define the d-Paley sum graph over
![]() $\mathbb {F}_q$
, denoted
$\mathbb {F}_q$
, denoted
![]() $GPS(q,d)$
, to be a graph with the vertex set being
$GPS(q,d)$
, to be a graph with the vertex set being
![]() $\mathbb {F}_q$
, and two vertices x and y are adjacent if
$\mathbb {F}_q$
, and two vertices x and y are adjacent if
![]() $x+y$
is a d-th power in
$x+y$
is a d-th power in
![]() $\mathbb {F}_q^*$
or
$\mathbb {F}_q^*$
or
![]() $x+y=0$
. Equivalently,
$x+y=0$
. Equivalently,
![]() $GPS(q,d)=CayS(\mathbb {F}_q, S_d \cup \{0\})$
. Now, we are ready to equivalently reformulate Theorems 1.6 and 1.7 using the graph theoretical language:
$GPS(q,d)=CayS(\mathbb {F}_q, S_d \cup \{0\})$
. Now, we are ready to equivalently reformulate Theorems 1.6 and 1.7 using the graph theoretical language:
Corollary 3.4 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $p \equiv 1 \ \pmod d$
be a prime. Then
$p \equiv 1 \ \pmod d$
be a prime. Then
Corollary 3.5 Let
![]() $d \geq 3$
. Let
$d \geq 3$
. Let
![]() $q \equiv 1 \ \pmod d$
be an odd prime power and a square. If
$q \equiv 1 \ \pmod d$
be an odd prime power and a square. If
![]() $d \nmid (\sqrt {q}+1)$
, then
$d \nmid (\sqrt {q}+1)$
, then
![]() $\omega (GPS(q,d))\leq \sqrt {q}-1$
. If
$\omega (GPS(q,d))\leq \sqrt {q}-1$
. If
![]() $d \mid (\sqrt {q}+1)$
, then
$d \mid (\sqrt {q}+1)$
, then
![]() $\omega (GPS(q,d))= \sqrt {q}$
and the each maximum clique if of the form
$\omega (GPS(q,d))= \sqrt {q}$
and the each maximum clique if of the form
![]() $\alpha \mathbb {F}_{\sqrt {q}}$
, where
$\alpha \mathbb {F}_{\sqrt {q}}$
, where
![]() $\alpha \in S_d$
.
$\alpha \in S_d$
.
Remark 3.6 The original conjecture due to van Lint and MacWilliams [Reference van Lint and MacWilliams34] is often formulated as the classification of maximum cliques in Paley graphs of square order. Its generalizations can be similarly viewed as the classification of maximum cliques in special Cayley graphs (such as generalized Paley graphs, Peisert graphs, and Peisert-type graphs) and a key ingredient for such generalizations is to view such graphs geometrically [Reference Asgarli and Yip2, Reference Blokhuis4, Reference Sziklai33]. The conjecture and its generalization are also known as the Erdős–Ko–Rado (EKR) theorem in these graphs, in the sense that each maximum clique in these graphs is a canonical clique, that is, a clique with a subfield structure, which corresponds to a line in the affine Galois plane. We refer to more discussions in [Reference Godsil and Meagher12, Section 5.9] and [Reference Asgarli and Yip2].
Corollary 3.5 can be viewed as the EKR theorem for d-Paley sum graphs. If
![]() $d \mid (\sqrt {q}+1)$
, then it is obvious that
$d \mid (\sqrt {q}+1)$
, then it is obvious that
![]() $\alpha \mathbb {F}_{\sqrt {q}}$
are maximum cliques (these cliques can be viewed as canonical cliques) and Corollary 3.5 implies there is no maximum non-canonical clique, which is reminiscent of the classical EKR theorem [Reference Erdős, Ko and Rado10]. Usually, Cayley sum graphs are much more difficult to study compared to Cayley graphs. Karen MeagherFootnote
3
remarked that proving EKR results for Cayley sum graphs requires different tools other than those known algebraic approaches for proving EKR results for Cayley graphs collected in her book joint with Godsil [Reference Godsil and Meagher12] mainly because Cayley sum graphs lose vertex-transitivity. She also pointed out that Corollary 3.5 appears to be the first instance of EKR results in a family of Cayley sum graphs.
$\alpha \mathbb {F}_{\sqrt {q}}$
are maximum cliques (these cliques can be viewed as canonical cliques) and Corollary 3.5 implies there is no maximum non-canonical clique, which is reminiscent of the classical EKR theorem [Reference Erdős, Ko and Rado10]. Usually, Cayley sum graphs are much more difficult to study compared to Cayley graphs. Karen MeagherFootnote
3
remarked that proving EKR results for Cayley sum graphs requires different tools other than those known algebraic approaches for proving EKR results for Cayley graphs collected in her book joint with Godsil [Reference Godsil and Meagher12] mainly because Cayley sum graphs lose vertex-transitivity. She also pointed out that Corollary 3.5 appears to be the first instance of EKR results in a family of Cayley sum graphs.
4 Applications to restricted sumset decompositions
Recall that our goal is to analyze whether a multiplicative subgroup
![]() $S_d$
can admit a restricted sumset decomposition, that is, whether there is
$S_d$
can admit a restricted sumset decomposition, that is, whether there is
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A \hat {+} A=S_d$
. In this section, we apply Proposition 3.1 and various additional ingredients to prove our main results. We first prove Theorem 1.4 and deduce Theorem 1.3 in Section 4.2. We then introduce more tools and prove Theorems 1.1 and 1.2.
$A \hat {+} A=S_d$
. In this section, we apply Proposition 3.1 and various additional ingredients to prove our main results. We first prove Theorem 1.4 and deduce Theorem 1.3 in Section 4.2. We then introduce more tools and prove Theorems 1.1 and 1.2.
4.1 The condition on sumset in Proposition 3.1
To apply Proposition 3.1, we need to analyze the possibility of
![]() $A+A=S_d \cup \{0\}$
or
$A+A=S_d \cup \{0\}$
or
![]() $A+A=S_d$
. The following proposition gives a sufficient condition for ruling out this possibility.
$A+A=S_d$
. The following proposition gives a sufficient condition for ruling out this possibility.
Proposition 4.1 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $p \equiv 1 \ \pmod d$
be a prime. Let q be a power of p such that
$p \equiv 1 \ \pmod d$
be a prime. Let q be a power of p such that
![]() $\frac {q-1}{d}\geq 3$
. Then for any
$\frac {q-1}{d}\geq 3$
. Then for any
![]() $A \subset \mathbb {F}_q$
,
$A \subset \mathbb {F}_q$
,
![]() $A+A \neq S_d$
and
$A+A \neq S_d$
and
![]() $A+A \neq S_d \cup \{0\}$
.
$A+A \neq S_d \cup \{0\}$
.
Proof The statement
![]() $A+A \neq S_d$
has already been proved in [Reference Yip37, Corollary 1.3]. Suppose otherwise that
$A+A \neq S_d$
has already been proved in [Reference Yip37, Corollary 1.3]. Suppose otherwise that
![]() $A+A=S_d \cup \{0\}$
. In this case, it is more difficult to derive a contradiction. In the following, we use a similar argument as in the proof of [Reference Yip37, Theorem 1.2] together with a few new ingredients.
$A+A=S_d \cup \{0\}$
. In this case, it is more difficult to derive a contradiction. In the following, we use a similar argument as in the proof of [Reference Yip37, Theorem 1.2] together with a few new ingredients.
For each
![]() $x \in A+A$
, let
$x \in A+A$
, let
![]() $r(x)$
be the number of pairs
$r(x)$
be the number of pairs
![]() $(a,a')$
such that
$(a,a')$
such that
![]() $a,a' \in A$
and
$a,a' \in A$
and
![]() $a+a'=x$
. Let
$a+a'=x$
. Let
![]() $\beta $
be the number of
$\beta $
be the number of
![]() $x \in (A+A)\setminus \{0\}$
such that
$x \in (A+A)\setminus \{0\}$
such that
![]() $r(x)=1$
. Observe the following:
$r(x)=1$
. Observe the following:
-
•
 $r(0)=|A \cap (-A)|$
. If
$r(0)=|A \cap (-A)|$
. If
 $a+a'=0$
, then
$a+a'=0$
, then
 $a'=-a \in A$
and thus
$a'=-a \in A$
and thus
 $a \in A \cap (-A)$
.
$a \in A \cap (-A)$
. -
•
 $\beta \leq |A|$
. Indeed, if
$\beta \leq |A|$
. Indeed, if
 $r(x)=1$
, then there exist
$r(x)=1$
, then there exist
 $a \in A$
such that
$a \in A$
such that
 $x=a+a$
. Otherwise, if there are
$x=a+a$
. Otherwise, if there are
 $a',a" \in A$
such that
$a',a" \in A$
such that
 $a' \neq a"$
and
$a' \neq a"$
and
 $a'+a"=x$
, then
$a'+a"=x$
, then
 $r(x) \geq 2$
since we also have
$r(x) \geq 2$
since we also have
 $a"+a'=x$
.
$a"+a'=x$
.
It follows that
 $$ \begin{align*} |A|^2&=\sum_{x \in A+A} r(x)\geq r(0)+\beta+2(|(A+A) \setminus \{0\}|-\beta) \\ &= |A \cap (-A)|+2|(A+A) \setminus \{0\}|-\beta \geq |A \cap (-A)|+2|(A+A) \setminus \{0\}|-|A|. \end{align*} $$
$$ \begin{align*} |A|^2&=\sum_{x \in A+A} r(x)\geq r(0)+\beta+2(|(A+A) \setminus \{0\}|-\beta) \\ &= |A \cap (-A)|+2|(A+A) \setminus \{0\}|-\beta \geq |A \cap (-A)|+2|(A+A) \setminus \{0\}|-|A|. \end{align*} $$
Therefore,
Suppose B is a subset of A such that
 $$ \begin{align} |B|>\frac{|A|+1}{2} \quad \text{ and } \quad \binom{|B|-1+\frac{q-1}{d}}{\frac{q-1}{d}}\not \equiv 0 \ \ \pmod p. \end{align} $$
$$ \begin{align} |B|>\frac{|A|+1}{2} \quad \text{ and } \quad \binom{|B|-1+\frac{q-1}{d}}{\frac{q-1}{d}}\not \equiv 0 \ \ \pmod p. \end{align} $$
Note that
![]() $A+B \subset A+A=S_d \cup \{0\}$
. Thus, Theorem 2.5 implies that
$A+B \subset A+A=S_d \cup \{0\}$
. Thus, Theorem 2.5 implies that
Adding up Equations (4.1) and (4.3) and simplifying, we obtain that
with equality holding only if
![]() $|A \cap (-A)|=|A \cap (-B)|$
. On the other hand, since
$|A \cap (-A)|=|A \cap (-B)|$
. On the other hand, since
![]() $|B|>\frac {|A|+1}{2}$
, we have
$|B|>\frac {|A|+1}{2}$
, we have
with equality holding only if
![]() $|A|=|A \cap (-A)|$
, that is,
$|A|=|A \cap (-A)|$
, that is,
![]() $-A=A$
. By comparing the above two estimates, we deduce that
$-A=A$
. By comparing the above two estimates, we deduce that
![]() $A=B$
and
$A=B$
and
![]() $-A=A$
. Thus, Equation (4.3) implies that
$-A=A$
. Thus, Equation (4.3) implies that
while Equation (4.1) implies that
It follows that
![]() $|A| \leq 2$
and thus
$|A| \leq 2$
and thus
![]() $|S_d|=|(A+A) \setminus \{0\}| \leq 2$
, contradicting the assumption that
$|S_d|=|(A+A) \setminus \{0\}| \leq 2$
, contradicting the assumption that
![]() $|S_d|=\frac {q-1}{d} \geq 3$
.
$|S_d|=\frac {q-1}{d} \geq 3$
.
It remains to construct a subset B of A with the property (4.2). Write
![]() $|A|-1=(c_k, c_{k-1}, \ldots , c_1,c_0)_p$
in base-p, that is,
$|A|-1=(c_k, c_{k-1}, \ldots , c_1,c_0)_p$
in base-p, that is,
![]() $|A|-1=\sum _{i=0}^k c_ip^i$
with
$|A|-1=\sum _{i=0}^k c_ip^i$
with
![]() $0 \leq c_i \leq p-1$
for each
$0 \leq c_i \leq p-1$
for each
![]() $0 \leq i \leq k$
and
$0 \leq i \leq k$
and
![]() $c_k \geq 1$
. Next, we construct B according to the size of
$c_k \geq 1$
. Next, we construct B according to the size of
![]() $c_k$
.
$c_k$
.
(1)
![]() $c_k \leq p-1-\frac {p-1}{d}$
. In this case, let B be an arbitrary subset of A with
$c_k \leq p-1-\frac {p-1}{d}$
. In this case, let B be an arbitrary subset of A with
![]() $|B|-1=(c_k,0, \ldots , 0)_p$
, that is,
$|B|-1=(c_k,0, \ldots , 0)_p$
, that is,
![]() $|B|=c_kp^k+1$
. It is easy to verify that
$|B|=c_kp^k+1$
. It is easy to verify that
![]() $\binom {|B|-1+\frac {q-1}{d}}{\frac {q-1}{d}} \not \equiv 0 \ \pmod p$
using Kummer’s theorem. Since
$\binom {|B|-1+\frac {q-1}{d}}{\frac {q-1}{d}} \not \equiv 0 \ \pmod p$
using Kummer’s theorem. Since
![]() $|A| \leq (c_k+1)p^k$
, we also have that
$|A| \leq (c_k+1)p^k$
, we also have that
![]() $2|B|>|A|+1$
.
$2|B|>|A|+1$
.
(2)
![]() $c_k> p-1-\frac {p-1}{d}$
. In this case, let B be an arbitrary subset of A with
$c_k> p-1-\frac {p-1}{d}$
. In this case, let B be an arbitrary subset of A with
 $$ \begin{align*}|B|-1=\bigg(\frac{(d-1)(p-1)}{d},\frac{(d-1)(p-1)}{d}, \ldots, \frac{(d-1)(p-1)}{d}\bigg)_p,\end{align*} $$
$$ \begin{align*}|B|-1=\bigg(\frac{(d-1)(p-1)}{d},\frac{(d-1)(p-1)}{d}, \ldots, \frac{(d-1)(p-1)}{d}\bigg)_p,\end{align*} $$
that is,
![]() $|B|=\frac {(d-1)(p-1)}{d} \cdot \sum _{i=0}^k p^i +1$
. Again, it is easy to verify that
$|B|=\frac {(d-1)(p-1)}{d} \cdot \sum _{i=0}^k p^i +1$
. Again, it is easy to verify that
![]() $\binom {|B|-1+\frac {q-1}{d}}{\frac {q-1}{d}} \not \equiv 0 \ \pmod p$
. Since
$\binom {|B|-1+\frac {q-1}{d}}{\frac {q-1}{d}} \not \equiv 0 \ \pmod p$
. Since
![]() $d \geq 2$
, it follows that
$d \geq 2$
, it follows that
![]() $2|B| \geq (p-1)\sum _{i=0}^k p^i +2= p^{k+1}+1\geq |A|+1$
, where equality holds only if
$2|B| \geq (p-1)\sum _{i=0}^k p^i +2= p^{k+1}+1\geq |A|+1$
, where equality holds only if
![]() $d=2$
and
$d=2$
and
![]() $|A|=p^{k+1}$
.
$|A|=p^{k+1}$
.
(3) It remains to consider the case that
![]() $d=2$
and
$d=2$
and
![]() $|A|=p^{k+1}$
. Equation (4.1) implies that
$|A|=p^{k+1}$
. Equation (4.1) implies that
![]() $q-1 \leq |A|^2+|A|-|A \cap (-A)|$
and thus
$q-1 \leq |A|^2+|A|-|A \cap (-A)|$
and thus
![]() $|A|\geq \sqrt {q}-1$
. On the other hand,
$|A|\geq \sqrt {q}-1$
. On the other hand,
![]() $|A|\leq \sqrt {q}$
, where equality holds only if
$|A|\leq \sqrt {q}$
, where equality holds only if
![]() $A=-A$
. Therefore, q is a square,
$A=-A$
. Therefore, q is a square,
![]() $|A|=\sqrt {q}$
and
$|A|=\sqrt {q}$
and
![]() $A=-A$
. Since q is odd,
$A=-A$
. Since q is odd,
![]() $0 \in A$
and
$0 \in A$
and
![]() $A \subset S_2 \cup \{0\}$
. It follows that
$A \subset S_2 \cup \{0\}$
. It follows that
![]() $A-A=A+A=S_2 \cup \{0\}$
. Let
$A-A=A+A=S_2 \cup \{0\}$
. Let
![]() $A'=a_0^{-1}A$
, where
$A'=a_0^{-1}A$
, where
![]() $a_0$
is a nonzero element of A. Then we have
$a_0$
is a nonzero element of A. Then we have
![]() $0,1 \in A'$
,
$0,1 \in A'$
,
![]() $|A'|=\sqrt {q}$
and
$|A'|=\sqrt {q}$
and
![]() $A'-A' \subset S_2 \cup \{0\}$
. Now the conjecture of van Lint and MacWilliams [Reference van Lint and MacWilliams34] mentioned in the introduction (first confirmed by Blokhuis [Reference Blokhuis4]) implies that
$A'-A' \subset S_2 \cup \{0\}$
. Now the conjecture of van Lint and MacWilliams [Reference van Lint and MacWilliams34] mentioned in the introduction (first confirmed by Blokhuis [Reference Blokhuis4]) implies that
![]() $A'=\mathbb {F}_{\sqrt {q}}$
and thus
$A'=\mathbb {F}_{\sqrt {q}}$
and thus
![]() $A=a_0\mathbb {F}_{\sqrt {q}}$
. However, this implies that
$A=a_0\mathbb {F}_{\sqrt {q}}$
. However, this implies that
![]() $A+A=a_0\mathbb {F}_{\sqrt {q}} \neq S_2 \cup \{0\}$
, a contradiction.
$A+A=a_0\mathbb {F}_{\sqrt {q}} \neq S_2 \cup \{0\}$
, a contradiction.
4.2 Proof of Theorem 1.4 and its consequences
Proposition 3.1 implies the following corollary on strong structural information on A, which will be crucial in the proof of our main results.
Corollary 4.2 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod d$
be an odd prime power. Assume that there is
$q \equiv 1 \ \pmod d$
be an odd prime power. Assume that there is
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A\hat {+}A=S_d$
while
$A\hat {+}A=S_d$
while
![]() $A+A \not \subset S_d \cup \{0\}$
. If
$A+A \not \subset S_d \cup \{0\}$
. If
![]() $|A|$
is odd or
$|A|$
is odd or
![]() $0 \in A$
, then A is a Sidon set with
$0 \in A$
, then A is a Sidon set with
![]() $\{2a: a \in A\} \cap S_d=\emptyset $
and
$\{2a: a \in A\} \cap S_d=\emptyset $
and
If
![]() $|A|$
is even, then
$|A|$
is even, then
 $$ \begin{align*}N=2\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil, \quad \text{and} \quad \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
$$ \begin{align*}N=2\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil, \quad \text{and} \quad \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
Proof Let
![]() $|A|=\{a_1,a_2, \ldots , a_N\}$
. Note that
$|A|=\{a_1,a_2, \ldots , a_N\}$
. Note that
![]() $A \hat {+} A=S_d$
implies that
$A \hat {+} A=S_d$
implies that
Next, we divide the discussion according to the following two cases.
(1) N is odd. Then Proposition 3.1 implies that
It follows from Equation (4.4) that
that is, A is a weak Sidon set (the sums
![]() $a_i+a_j$
, for
$a_i+a_j$
, for
![]() $i<j$
, are all distinct). Moreover,
$i<j$
, are all distinct). Moreover,
![]() $2a \not \in S_d \cup \{0\}$
for each
$2a \not \in S_d \cup \{0\}$
for each
![]() $a \in A$
. Since q is odd, it is clear that
$a \in A$
. Since q is odd, it is clear that
![]() $2a_i \neq 2a_j$
for
$2a_i \neq 2a_j$
for
![]() $i \neq j$
. Thus, we conclude that A is a Sidon set.
$i \neq j$
. Thus, we conclude that A is a Sidon set.
(2) N is even and
![]() $0 \in A$
. Then Proposition 3.1 implies that
$0 \in A$
. Then Proposition 3.1 implies that
We can argue similarly to (1) to deduce the desired properties of A.
(3) N is even and
![]() $0 \not \in A$
. Then we have the weaker estimate
$0 \not \in A$
. Then we have the weaker estimate
from Proposition 3.1. It follows from Equation (4.4) that
equivalently,
 $$ \begin{align*}\frac{N}{2}-\frac{1}{2}< \sqrt{\frac{q-1}{2d}}<\frac{N}{2}-\frac{1}{4}. \end{align*} $$
$$ \begin{align*}\frac{N}{2}-\frac{1}{2}< \sqrt{\frac{q-1}{2d}}<\frac{N}{2}-\frac{1}{4}. \end{align*} $$
Recall that N is even, so
![]() $\frac {N}{2}$
is an integer. Thus, N is uniquely determined by
$\frac {N}{2}$
is an integer. Thus, N is uniquely determined by
 $$ \begin{align} N=2\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil, \quad \text{and} \quad \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align} $$
$$ \begin{align} N=2\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil, \quad \text{and} \quad \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align} $$
Next, we present the proof of Theorem 1.4.
Proof of Theorem 1.4
Let
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A\hat {+}A=S_d$
. In view of Corollary 4.2, it suffices to show that
$A\hat {+}A=S_d$
. In view of Corollary 4.2, it suffices to show that
![]() $A+A \not \subset S_d \cup \{0\}$
. Equivalently, it suffices to show that
$A+A \not \subset S_d \cup \{0\}$
. Equivalently, it suffices to show that
![]() $A+A \neq S_d$
and
$A+A \neq S_d$
and
![]() $A+A \neq S_d \cup \{0\}$
, which have been proved in Proposition 4.1.
$A+A \neq S_d \cup \{0\}$
, which have been proved in Proposition 4.1.
With Theorem 1.4, we deduce two interesting consequences below.
Proof of Theorem 1.3
Let
![]() $q=p^{2r}$
. Assume that there is
$q=p^{2r}$
. Assume that there is
![]() $A \subset \mathbb {F}_q$
with
$A \subset \mathbb {F}_q$
with
![]() $A \hat {+} A= S_d$
.
$A \hat {+} A= S_d$
.
(1) If
![]() $|A|$
is odd, then Theorem 1.4 implies that
$|A|$
is odd, then Theorem 1.4 implies that
![]() $q=p^{2r}=k^2 |A|(|A|-1)+1.$
Thus,
$q=p^{2r}=k^2 |A|(|A|-1)+1.$
Thus,
It follows that
![]() $(2p^r+2k|A|-k)$
is a divisor of
$(2p^r+2k|A|-k)$
is a divisor of
![]() $(k^2-4)$
. In particular,
$(k^2-4)$
. In particular,
![]() $p \leq 2p^r+2k|A|-k \leq k^2-4<d$
, violating the assumption that
$p \leq 2p^r+2k|A|-k \leq k^2-4<d$
, violating the assumption that
![]() $p \equiv 1 \ \pmod d$
.
$p \equiv 1 \ \pmod d$
.
(2) If
![]() $|A|$
is even, then Theorem 1.4 implies that
$|A|$
is even, then Theorem 1.4 implies that
 $$ \begin{align*}\frac{p^r-1}{2k}+\frac{\sqrt{p^{2r}-1}-(p^r-1)}{2k}=\frac{\sqrt{p^{2r}-1}}{2k}=\sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
$$ \begin{align*}\frac{p^r-1}{2k}+\frac{\sqrt{p^{2r}-1}-(p^r-1)}{2k}=\frac{\sqrt{p^{2r}-1}}{2k}=\sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
Since
![]() $p \equiv 1 \ \pmod d$
and
$p \equiv 1 \ \pmod d$
and
![]() $d=2k^2$
, it follows that
$d=2k^2$
, it follows that
![]() $2k \mid (p^r-1)$
and thus
$2k \mid (p^r-1)$
and thus
 $$ \begin{align*}\frac{\sqrt{p^{2r}-1}-(p^r-1)}{2k}\in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
$$ \begin{align*}\frac{\sqrt{p^{2r}-1}-(p^r-1)}{2k}\in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align*} $$
However, the number on the left-hand side is in
![]() $(0,\frac {1}{2k})$
, while
$(0,\frac {1}{2k})$
, while
![]() $\frac {1}{2k}\leq \frac {1}{6}<\frac {1}{2}$
, a contradiction.
$\frac {1}{2k}\leq \frac {1}{6}<\frac {1}{2}$
, a contradiction.
Proof of Corollary 1.5
Let
![]() $p \equiv 1 \ \pmod d$
to be a prime and let
$p \equiv 1 \ \pmod d$
to be a prime and let
![]() $A \subset \mathbb {F}_{p^k}$
such that
$A \subset \mathbb {F}_{p^k}$
such that
![]() $A\hat {+}A=S_d(\mathbb {F}_{p^k})$
. Assume that
$A\hat {+}A=S_d(\mathbb {F}_{p^k})$
. Assume that
![]() $|A|$
is odd or
$|A|$
is odd or
![]() $0 \in A$
. Then Theorem 1.4 implies that
$0 \in A$
. Then Theorem 1.4 implies that
First, consider the case
![]() $d=8$
. Then we have
$d=8$
. Then we have
![]() $p^k=4|A|(|A|-1)+1=(2|A|-1)^2$
, which is impossible since k is odd.
$p^k=4|A|(|A|-1)+1=(2|A|-1)^2$
, which is impossible since k is odd.
Next, we assume that
![]() $d \neq 8$
. Note that
$d \neq 8$
. Note that
is a smooth affine curve with genus
![]() $g=\lceil k/2 \rceil -1 \geq 1$
since
$g=\lceil k/2 \rceil -1 \geq 1$
since
![]() $f(x)=\frac {8}{d}(x^k-1)+1$
has no repeated root when
$f(x)=\frac {8}{d}(x^k-1)+1$
has no repeated root when
![]() $d \neq 8$
(see for example [Reference Hindry and Silverman17, Section A.4.5]). Thus, Siegel’s theorem on integral points [Reference Hindry and Silverman17, Theorem D.9.1] implies the curve C only has finitely many integral points. On the other hand, note that
$d \neq 8$
(see for example [Reference Hindry and Silverman17, Section A.4.5]). Thus, Siegel’s theorem on integral points [Reference Hindry and Silverman17, Theorem D.9.1] implies the curve C only has finitely many integral points. On the other hand, note that
![]() $(p, 2|A|-1)$
is an integral point on the curve C, thus p is upper bounded by a constant
$(p, 2|A|-1)$
is an integral point on the curve C, thus p is upper bounded by a constant
![]() $p_0$
depending only on d and k.
$p_0$
depending only on d and k.
4.3 A refinement on Proposition 3.1 when
 $|A|$
is even
$|A|$
is even
When
![]() $|A|$
is even and
$|A|$
is even and
![]() $0 \notin A$
, Proposition 3.1 is not strong enough for our purpose. Thus, we are led to pay extra attention to this more challenging situation and we establish the following proposition.
$0 \notin A$
, Proposition 3.1 is not strong enough for our purpose. Thus, we are led to pay extra attention to this more challenging situation and we establish the following proposition.
Proposition 4.3 Let
![]() $d \geq 2$
and let
$d \geq 2$
and let
![]() $q \equiv 1 \ \pmod d$
be an odd prime power. Assume that there is
$q \equiv 1 \ \pmod d$
be an odd prime power. Assume that there is
![]() $A \subset \mathbb {F}_q$
with
$A \subset \mathbb {F}_q$
with
![]() $|A|=N$
even, such that
$|A|=N$
even, such that
![]() $A\hat {+}A=S_d$
while
$A\hat {+}A=S_d$
while
![]() $A+A \not \subset S_d \cup \{0\}$
. Then the following conditions necessarily hold:
$A+A \not \subset S_d \cup \{0\}$
. Then the following conditions necessarily hold:
-
•
 $\binom {m+\frac {q-1}{d}}{m+1} \not \equiv 0 \ \pmod p$
, where
$\binom {m+\frac {q-1}{d}}{m+1} \not \equiv 0 \ \pmod p$
, where
 $m=\frac {N-2}{2}$
.
$m=\frac {N-2}{2}$
. -
•
 $\{2a: a \in A\} \cap S_d=\emptyset $
.
$\{2a: a \in A\} \cap S_d=\emptyset $
. -
• If
 $d=2$
, then
$d=2$
, then
 $q \equiv 3,5 \ \pmod 8$
and A is a Sidon set with
$q \equiv 3,5 \ \pmod 8$
and A is a Sidon set with
 $0 \in A$
.
$0 \in A$
.
Proof Let
![]() $A=\{a_1, a_2, \ldots , a_N\}$
and let
$A=\{a_1, a_2, \ldots , a_N\}$
and let
![]() $m=\frac {N-2}{2}$
. Consider instead the following auxiliary polynomial:
$m=\frac {N-2}{2}$
. Consider instead the following auxiliary polynomial:
 $$ \begin{align} f(x)=-(-1)^{m+1}+\sum_{i=1}^N c_i (x+a_i)^{m+\frac{q-1}{d}} (x-a_i)^{m+1}\in \mathbb{F}_q[x], \end{align} $$
$$ \begin{align} f(x)=-(-1)^{m+1}+\sum_{i=1}^N c_i (x+a_i)^{m+\frac{q-1}{d}} (x-a_i)^{m+1}\in \mathbb{F}_q[x], \end{align} $$
where
![]() $c_1,c_2,...,c_N$
is the unique solution of the following system of equations:
$c_1,c_2,...,c_N$
is the unique solution of the following system of equations:
 $$ \begin{align} \left\{ \begin{array}{ll} \sum_{i=1}^N c_i a_i^j=0, \quad &0 \leq j \leq 2m=N-2\\\\ \sum_{i=1}^N c_i a_i^{N-1}=1. \end{array}\right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} \sum_{i=1}^N c_i a_i^j=0, \quad &0 \leq j \leq 2m=N-2\\\\ \sum_{i=1}^N c_i a_i^{N-1}=1. \end{array}\right. \end{align} $$
With this new polynomial (4.6), similar arguments as in the proof of Proposition 3.1 lead to the following.
-
•
 $\deg f \leq \frac {q-1}{d}$
.
$\deg f \leq \frac {q-1}{d}$
. -
•
 $f(a_j)=0$
for each
$f(a_j)=0$
for each
 $1 \leq j \leq N.$
$1 \leq j \leq N.$
-
• An analogous claim, namely
(4.8)holds for each $$ \begin{align} \sum_{i=1}^N c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^{m+1}](a_j)=0. \end{align} $$
$$ \begin{align} \sum_{i=1}^N c_i E^{(k_1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(k_2)}[(x-a_i)^{m+1}](a_j)=0. \end{align} $$
 $1 \leq j \leq N$
, provided that
$1 \leq j \leq N$
, provided that
 $0 \leq k_1,k_2\leq m$
and
$0 \leq k_1,k_2\leq m$
and
 $1 \leq k_1+k_2 \leq m+1$
.
$1 \leq k_1+k_2 \leq m+1$
.
-
• Via claim (4.8), Lemma 2.3 then allows us to deduce that for each
 $1 \leq j \leq N$
, the multiplicity of
$1 \leq j \leq N$
, the multiplicity of
 $a_j$
as a root of f is at least
$a_j$
as a root of f is at least
 $m+1$
by showing that
$m+1$
by showing that
 $E^{(r)}f(a_j)=0$
for
$E^{(r)}f(a_j)=0$
for
 $1 \leq r \leq m$
.
$1 \leq r \leq m$
.
If f is not identically zero, then we obtain the inequality
which contradicts inequality (4.4) (a consequence of
![]() $A \hat {+} A=S_d$
). Thus, we deduce that the polynomial f we constructed in Equation (4.6) must be identically zero. Next, we use this strong algebraic condition to deduce some structural information of A.
$A \hat {+} A=S_d$
). Thus, we deduce that the polynomial f we constructed in Equation (4.6) must be identically zero. Next, we use this strong algebraic condition to deduce some structural information of A.
Since f is identically zero, in particular,
![]() $E^{(m+1)} f (a_j)=0$
for each
$E^{(m+1)} f (a_j)=0$
for each
![]() $1 \leq j \leq N$
. For each
$1 \leq j \leq N$
. For each
![]() $1\leq j \leq N$
, note that claim (4.8) and Lemma 2.3 together imply that
$1\leq j \leq N$
, note that claim (4.8) and Lemma 2.3 together imply that
 $$ \begin{align} E^{(m+1)} f (a_j) &= \sum_{i=1}^N c_i E^{(0)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(m+1)}[(x-a_i)^{m+1}](a_j) \notag\\ &\quad +\binom{m+\frac{q-1}{d}}{m+1} \sum_{i=1}^N c_i E^{(m+1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(0)}[(x-a_i)^{m+1}](a_j) \notag\\ &= \sum_{i=1}^N c_i (a_j+a_i)^{m+\frac{q-1}{d}} +\binom{m+\frac{q-1}{d}}{m+1} \sum_{i=1}^N c_i (a_j+a_i)^{\frac{q-1}{d}-1} (a_j-a_i)^{m+1}. \end{align} $$
$$ \begin{align} E^{(m+1)} f (a_j) &= \sum_{i=1}^N c_i E^{(0)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(m+1)}[(x-a_i)^{m+1}](a_j) \notag\\ &\quad +\binom{m+\frac{q-1}{d}}{m+1} \sum_{i=1}^N c_i E^{(m+1)}[(x+a_i)^{m+\frac{q-1}{d}}](a_j) \cdot E^{(0)}[(x-a_i)^{m+1}](a_j) \notag\\ &= \sum_{i=1}^N c_i (a_j+a_i)^{m+\frac{q-1}{d}} +\binom{m+\frac{q-1}{d}}{m+1} \sum_{i=1}^N c_i (a_j+a_i)^{\frac{q-1}{d}-1} (a_j-a_i)^{m+1}. \end{align} $$
In the following discussion, let
![]() $1 \leq j \leq N$
be such that
$1 \leq j \leq N$
be such that
![]() $a_j \neq 0$
. The same computation as in Equation (3.6) shows that
$a_j \neq 0$
. The same computation as in Equation (3.6) shows that
 $$ \begin{align*}\sum_{i=1}^N c_i (a_j+a_i)^{m+\frac{q-1}{d}}=c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg). \end{align*} $$
$$ \begin{align*}\sum_{i=1}^N c_i (a_j+a_i)^{m+\frac{q-1}{d}}=c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg). \end{align*} $$
Also note that for each
![]() $i \neq j$
,
$i \neq j$
,
 $$ \begin{align*}(a_j+a_i)^{\frac{q-1}{d}-1} (a_j-a_i)^{m+1}=\frac{(a_j-a_i)^{m+1}}{a_j+a_i}, \end{align*} $$
$$ \begin{align*}(a_j+a_i)^{\frac{q-1}{d}-1} (a_j-a_i)^{m+1}=\frac{(a_j-a_i)^{m+1}}{a_j+a_i}, \end{align*} $$
and the above equation holds even when
![]() $i=j$
and
$i=j$
and
![]() $a_j=0$
, since both sides are zero. In view of system (4.7), we have the following:
$a_j=0$
, since both sides are zero. In view of system (4.7), we have the following:
 $$ \begin{align*} \sum_{i=1}^N c_i \frac{(a_j-a_i)^{m+1}}{a_j+a_i} &=\sum_{i=1}^N c_i \frac{(2a_j-(a_j+a_i))^{m+1}}{a_j+a_i}\\ &= \sum_{k=0}^{m+1} \binom{m+1}{k} (2a_j)^k (-1)^{m+1-k} \bigg(\sum_{i=1}^N c_i (a_j+a_i)^{m-k}\bigg)\\ &=(2a_j)^{m+1} \sum_{i=1}^N \frac{c_i}{a_j+a_i}. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^N c_i \frac{(a_j-a_i)^{m+1}}{a_j+a_i} &=\sum_{i=1}^N c_i \frac{(2a_j-(a_j+a_i))^{m+1}}{a_j+a_i}\\ &= \sum_{k=0}^{m+1} \binom{m+1}{k} (2a_j)^k (-1)^{m+1-k} \bigg(\sum_{i=1}^N c_i (a_j+a_i)^{m-k}\bigg)\\ &=(2a_j)^{m+1} \sum_{i=1}^N \frac{c_i}{a_j+a_i}. \end{align*} $$
Therefore, using the above three equations, Equation (4.9) simplifies to
 $$ \begin{align} 0=E^{(m+1)} f (a_j)=c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg) +\binom{m+\frac{q-1}{d}}{m+1} (2a_j)^{m+1} \sum_{i=1}^N \frac{c_i}{a_j+a_i}. \end{align} $$
$$ \begin{align} 0=E^{(m+1)} f (a_j)=c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg) +\binom{m+\frac{q-1}{d}}{m+1} (2a_j)^{m+1} \sum_{i=1}^N \frac{c_i}{a_j+a_i}. \end{align} $$
Using the formula for the inverse of a Vandermonde matrix (see, for example, [Reference Horn and Johnson18, Section 0.9.11]), it is easy to verify that
 $$ \begin{align*}c_i=\bigg(\prod_{\substack{1 \leq k \leq N\\k \neq i}} (a_i-a_k)\bigg)^{-1}. \end{align*} $$
$$ \begin{align*}c_i=\bigg(\prod_{\substack{1 \leq k \leq N\\k \neq i}} (a_i-a_k)\bigg)^{-1}. \end{align*} $$
Consider the polynomial
 $$ \begin{align*}g(x)=\sum_{i=1}^N c_i\prod_{k \neq i} (x+a_k)=\sum_{i=1}^N \frac{\prod_{k \neq i} (x+a_k)}{\prod_{k \neq i} (a_i-a_k)} \in \mathbb{F}_q[x]. \end{align*} $$
$$ \begin{align*}g(x)=\sum_{i=1}^N c_i\prod_{k \neq i} (x+a_k)=\sum_{i=1}^N \frac{\prod_{k \neq i} (x+a_k)}{\prod_{k \neq i} (a_i-a_k)} \in \mathbb{F}_q[x]. \end{align*} $$
Note that g has degree at most
![]() $N-1$
, and for each
$N-1$
, and for each
![]() $1 \leq i \leq N$
, we have
$1 \leq i \leq N$
, we have
![]() $g(-a_i)=(-1)^{N-1}=-1$
. Therefore,
$g(-a_i)=(-1)^{N-1}=-1$
. Therefore,
![]() $g \equiv -1$
and thus
$g \equiv -1$
and thus
 $$ \begin{align*}\sum_{i=1}^N \frac{c_i}{a_j+a_i}=\frac{g(a_j)}{\prod_{i=1}^N (a_j+a_i)}=\frac{-1}{\prod_{i=1}^N (a_j+a_i)}. \end{align*} $$
$$ \begin{align*}\sum_{i=1}^N \frac{c_i}{a_j+a_i}=\frac{g(a_j)}{\prod_{i=1}^N (a_j+a_i)}=\frac{-1}{\prod_{i=1}^N (a_j+a_i)}. \end{align*} $$
As a summary, if
![]() $a_j \neq 0$
, we have shown that
$a_j \neq 0$
, we have shown that
 $$ \begin{align*} c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg) =\binom{m+\frac{q-1}{d}}{m+1} (2a_j)^{m+1} \frac{1}{\prod_{i=1}^N (a_j+a_i)}, \end{align*} $$
$$ \begin{align*} c_j (2a_j)^m \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg) =\binom{m+\frac{q-1}{d}}{m+1} (2a_j)^{m+1} \frac{1}{\prod_{i=1}^N (a_j+a_i)}, \end{align*} $$
equivalently
 $$ \begin{align} c_j \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg) \cdot \prod_{i=1}^N (a_j+a_i)= \binom{m+\frac{q-1}{d}}{m+1} \cdot 2a_j. \end{align} $$
$$ \begin{align} c_j \bigg((2a_j)^{\frac{q-1}{d}}-1\bigg) \cdot \prod_{i=1}^N (a_j+a_i)= \binom{m+\frac{q-1}{d}}{m+1} \cdot 2a_j. \end{align} $$
Since
![]() $A+A \not \subset S_d \cup \{0\}$
, there is
$A+A \not \subset S_d \cup \{0\}$
, there is
![]() $1\leq j_0\leq N$
such that
$1\leq j_0\leq N$
such that
![]() $2a_{j_0} \not \in S_d \cup \{0\}$
. By setting
$2a_{j_0} \not \in S_d \cup \{0\}$
. By setting
![]() $j=j_0$
in Equation (4.11), it follows that
$j=j_0$
in Equation (4.11), it follows that
![]() $\binom {m+\frac {q-1}{d}}{m+1}\neq 0$
. Now if
$\binom {m+\frac {q-1}{d}}{m+1}\neq 0$
. Now if
![]() $a_j \neq 0$
, Equation (4.11) implies that
$a_j \neq 0$
, Equation (4.11) implies that
![]() $(2a_j)^{\frac {q-1}{d}}\neq 1$
, that is,
$(2a_j)^{\frac {q-1}{d}}\neq 1$
, that is,
![]() $2a_j \notin S_d$
. Therefore,
$2a_j \notin S_d$
. Therefore,
![]() $\{2a: a \in A\} \cap S_d=\emptyset $
.
$\{2a: a \in A\} \cap S_d=\emptyset $
.
Finally, assume that
![]() $d=2$
. We have
$d=2$
. We have
 $$ \begin{align*} 0=f(0) &= -(-1)^{m+1}+\sum_{i=1}^N a_i^{m+\frac{q-1}{2}} (-a_i)^{m+1}\\ &= -(-1)^{m+1}+ (-1)^{m+1} \cdot \sum_{i=1}^N c_i a_i^{N-1+\frac{q-1}{2}}. \end{align*} $$
$$ \begin{align*} 0=f(0) &= -(-1)^{m+1}+\sum_{i=1}^N a_i^{m+\frac{q-1}{2}} (-a_i)^{m+1}\\ &= -(-1)^{m+1}+ (-1)^{m+1} \cdot \sum_{i=1}^N c_i a_i^{N-1+\frac{q-1}{2}}. \end{align*} $$
In view of the equation
![]() $\sum _{i=1}^N c_i a_i^{N-1}=1$
in system (4.7), we have
$\sum _{i=1}^N c_i a_i^{N-1}=1$
in system (4.7), we have
 $$ \begin{align*}\sum_{i=1}^N c_i a_i^{N-1+\frac{q-1}{2}}=\sum_{i=1}^N c_i a_i^{N-1}=1. \end{align*} $$
$$ \begin{align*}\sum_{i=1}^N c_i a_i^{N-1+\frac{q-1}{2}}=\sum_{i=1}^N c_i a_i^{N-1}=1. \end{align*} $$
Therefore,
![]() $\sum ^* c_i a_i^{N-1}=1$
, where the sum is over those i such that
$\sum ^* c_i a_i^{N-1}=1$
, where the sum is over those i such that
![]() $a_i \in S_2$
. In particular, there is
$a_i \in S_2$
. In particular, there is
![]() $1\leq k\leq N$
such that
$1\leq k\leq N$
such that
![]() $a_k \in S_2$
. If
$a_k \in S_2$
. If
![]() $q \equiv \pm 1 \ \pmod 8$
, then
$q \equiv \pm 1 \ \pmod 8$
, then
![]() $2 \in S_2$
and thus
$2 \in S_2$
and thus
![]() $2a_k \in S_2$
, contradicting the previous necessary condition. Thus, we must have
$2a_k \in S_2$
, contradicting the previous necessary condition. Thus, we must have
![]() $q \equiv 3,5 \ \pmod 8$
so that
$q \equiv 3,5 \ \pmod 8$
so that
![]() $2 \not \in S_2$
. It follows that
$2 \not \in S_2$
. It follows that
![]() $A \subset S_2 \cup \{0\}$
since
$A \subset S_2 \cup \{0\}$
since
![]() $2 \not \in S_2$
and
$2 \not \in S_2$
and
![]() $\{2a: a \in A\} \cap S_2=\emptyset $
.
$\{2a: a \in A\} \cap S_2=\emptyset $
.
Assume that
![]() $0 \not \in A$
so that
$0 \not \in A$
so that
![]() $A \subset S_2$
. Set
$A \subset S_2$
. Set
![]() $A'=A \cup \{0\}$
. We still have
$A'=A \cup \{0\}$
. We still have
![]() $A' \hat {+}A'=S_2$
since
$A' \hat {+}A'=S_2$
since
![]() $A \subset S_2$
. Since
$A \subset S_2$
. Since
![]() $|A|$
is even, it follows that
$|A|$
is even, it follows that
![]() $|A'|$
is odd and
$|A'|$
is odd and
![]() $A'$
is a Sidon set by Corollary 4.2. In particular, for each
$A'$
is a Sidon set by Corollary 4.2. In particular, for each
![]() $a \in A$
, we have
$a \in A$
, we have
![]() $a=0+a \not \in A+A$
while
$a=0+a \not \in A+A$
while
![]() $a \in S_2$
, which implies that
$a \in S_2$
, which implies that
![]() $A\hat {+}A\neq S_2$
, a contradiction. Therefore, we must have
$A\hat {+}A\neq S_2$
, a contradiction. Therefore, we must have
![]() $0 \in A$
. Consequently, Corollary 4.2 implies that A is a Sidon set.
$0 \in A$
. Consequently, Corollary 4.2 implies that A is a Sidon set.
4.4 Proof of Theorem 1.1
Proof of Theorem 1.1
Let
![]() $q=p^r>13$
and let
$q=p^r>13$
and let
![]() $A \subset \mathbb {F}_q$
. Suppose otherwise that
$A \subset \mathbb {F}_q$
. Suppose otherwise that
![]() $A \hat {+} A=S_2$
. Let
$A \hat {+} A=S_2$
. Let
![]() $|A|=N$
. By Proposition 4.1, Corollary 4.2, and Proposition 4.3, we deduce that A is a Sidon set and
$|A|=N$
. By Proposition 4.1, Corollary 4.2, and Proposition 4.3, we deduce that A is a Sidon set and
![]() $q=p^r=N^2-N+1$
. If
$q=p^r=N^2-N+1$
. If
![]() $r=1$
, then
$r=1$
, then
![]() $q=p$
, and the possibility that
$q=p$
, and the possibility that
![]() $A \hat {+} A =S_2$
has been ruled out by Shkredov [Reference Shkredov27, Theorem 1.2].
$A \hat {+} A =S_2$
has been ruled out by Shkredov [Reference Shkredov27, Theorem 1.2].
Next, we consider the case
![]() $r \geq 2$
. It turns out that
$r \geq 2$
. It turns out that
![]() $p^r=N(N-1)+1$
(where
$p^r=N(N-1)+1$
(where
![]() $r \geq 2$
) is a special case of the well-studied Nagell–Ljunggren equation. A classical result of Nagell [Reference Nagell22] (see also the survey [Reference Bugeaud and Mignotte5] by Bugeaud and Mignotte) implies that the only solution to
$r \geq 2$
) is a special case of the well-studied Nagell–Ljunggren equation. A classical result of Nagell [Reference Nagell22] (see also the survey [Reference Bugeaud and Mignotte5] by Bugeaud and Mignotte) implies that the only solution to
where
![]() $r \geq 2$
is
$r \geq 2$
is
![]() $(p,r, N)=(7,3,19)$
. Thus,
$(p,r, N)=(7,3,19)$
. Thus,
![]() $q=343$
and
$q=343$
and
![]() $|A|=N=19$
. However, in this case, a simple code via SageMath indicates that such A does not exist; in fact, the largest
$|A|=N=19$
. However, in this case, a simple code via SageMath indicates that such A does not exist; in fact, the largest
![]() $B \subset \mathbb {F}_{343}$
such that
$B \subset \mathbb {F}_{343}$
such that
![]() $B \hat {+}B \subset S_2$
has size
$B \hat {+}B \subset S_2$
has size
![]() $10$
. This completes the proof.
$10$
. This completes the proof.
Remark 4.4 When
![]() $q \in \{3,7,13\}$
, as already shown by Shkredov [Reference Shkredov27, Theorem 1.2], there is
$q \in \{3,7,13\}$
, as already shown by Shkredov [Reference Shkredov27, Theorem 1.2], there is
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A \hat {+} A=S_2$
. Thus, from the above proof, we can further deduce that if q is an odd prime power and
$A \hat {+} A=S_2$
. Thus, from the above proof, we can further deduce that if q is an odd prime power and
![]() $A \subset \mathbb {F}_q$
such that
$A \subset \mathbb {F}_q$
such that
![]() $A\hat {+}A= S_2$
, then the only possibilities are the following:
$A\hat {+}A= S_2$
, then the only possibilities are the following:
-
•
 $q=3, A=\{0,1\}$
.
$q=3, A=\{0,1\}$
. -
•
 $q=7, A=\{3,5,6\}$
.
$q=7, A=\{3,5,6\}$
. -
•
 $q=13$
,
$q=13$
,
 $A=\{0,1,3,9\}$
and
$A=\{0,1,3,9\}$
and
 $A=\{0,4,10,12\}$
.
$A=\{0,4,10,12\}$
.
Note that in each of the above cases, A is a Sidon set, and
![]() $q=|A|^2-|A|+1$
.
$q=|A|^2-|A|+1$
.
4.5 Proof of Theorem 1.2
Let
![]() $\mathcal {P}$
be the set of primes. For
$\mathcal {P}$
be the set of primes. For
![]() $d \geq 2$
, we define
$d \geq 2$
, we define
![]() $\mathcal {P}_d=\{p \in \mathcal {P}: p \equiv 1 \ \pmod d\}$
. To prove Theorem 1.2, we need the following result on uniform distribution due to Bergelson et. al. [Reference Bergelson, Kolesnik, Madritsch, Son and Tichy3, Corollary 2.3].
$\mathcal {P}_d=\{p \in \mathcal {P}: p \equiv 1 \ \pmod d\}$
. To prove Theorem 1.2, we need the following result on uniform distribution due to Bergelson et. al. [Reference Bergelson, Kolesnik, Madritsch, Son and Tichy3, Corollary 2.3].
Lemma 4.5 (Bergelson et. al.Footnote 4 )
Let
![]() $0 <\theta _1 <\theta _2 < \cdots < \theta _\ell $
and let
$0 <\theta _1 <\theta _2 < \cdots < \theta _\ell $
and let
![]() $\gamma _1, \gamma _2, \ldots , \gamma _\ell $
be nonzero real numbers such that
$\gamma _1, \gamma _2, \ldots , \gamma _\ell $
be nonzero real numbers such that
![]() $\gamma _j \not \in \mathbb {Q}$
if
$\gamma _j \not \in \mathbb {Q}$
if
![]() $\theta _j \in \mathbb {N}$
. Then for any
$\theta _j \in \mathbb {N}$
. Then for any
![]() $h \in \mathbb {Z}$
and positive integer d, the sequence
$h \in \mathbb {Z}$
and positive integer d, the sequence
 $$ \begin{align*}\bigg(\big(\gamma_1 (p-h)^{\theta_1},\gamma_2 (p-h)^{\theta_2}, \ldots, \gamma_\ell (p-h)^{\theta_\ell}\big)\bigg)_{p \in \mathcal{P}_d}\end{align*} $$
$$ \begin{align*}\bigg(\big(\gamma_1 (p-h)^{\theta_1},\gamma_2 (p-h)^{\theta_2}, \ldots, \gamma_\ell (p-h)^{\theta_\ell}\big)\bigg)_{p \in \mathcal{P}_d}\end{align*} $$
is equidistributed modulo
![]() $1$
in the
$1$
in the
![]() $\ell $
-dimensional torus
$\ell $
-dimensional torus
![]() $\mathbb {T}^\ell =\mathbb {R}^\ell /\mathbb {Z}^\ell $
.
$\mathbb {T}^\ell =\mathbb {R}^\ell /\mathbb {Z}^\ell $
.
Now we use the tools developed in this section to establish Theorem 1.2.
Proof of Theorem 1.2
Let
Our aim is to show the relative upper density of
![]() $\mathcal {B}_d \subset \mathcal {P}_d$
is at most
$\mathcal {B}_d \subset \mathcal {P}_d$
is at most
![]() $\frac {1}{4} \cdot (\frac {d-1}{d})^r$
.
$\frac {1}{4} \cdot (\frac {d-1}{d})^r$
.
We first consider the case where s is odd. In this case,
![]() $s=2r+1$
. For simplicity, for each
$s=2r+1$
. For simplicity, for each
![]() $p \in \mathcal {P}_d$
, we write
$p \in \mathcal {P}_d$
, we write
![]() $q=p^{2r+1}$
and
$q=p^{2r+1}$
and
 $$ \begin{align*}\alpha_p=\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil. \end{align*} $$
$$ \begin{align*}\alpha_p=\bigg\lceil \sqrt{\frac{q-1}{2d}} \bigg \rceil. \end{align*} $$
Let
![]() $p \in \mathcal {B}_d$
. Then there is
$p \in \mathcal {B}_d$
. Then there is
![]() $A \subset \mathbb {F}_q$
with
$A \subset \mathbb {F}_q$
with
![]() $A\hat {+}A=S_d$
. By Proposition 4.1,
$A\hat {+}A=S_d$
. By Proposition 4.1,
![]() $A+A \not \subset S_d \cup \{0\}$
. Let
$A+A \not \subset S_d \cup \{0\}$
. Let
![]() $|A|=N$
.
$|A|=N$
.
(1) If N is odd, then Theorem 1.4 implies that
(2) If N is even, then Theorem 1.4 implies that
![]() $N=2\alpha _p$
and
$N=2\alpha _p$
and
 $$ \begin{align} \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align} $$
$$ \begin{align} \sqrt{\frac{q-1}{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1. \end{align} $$
Let
![]() $m=\frac {N-2}{2}$
. By Proposition 4.1,
$m=\frac {N-2}{2}$
. By Proposition 4.1,
![]() $A+A \not \subset S_d \cup \{0\}$
so that we can apply Proposition 4.3 to deduce that
$A+A \not \subset S_d \cup \{0\}$
so that we can apply Proposition 4.3 to deduce that
 $$ \begin{align*}\binom{m+\frac{q-1}{d}}{m+1} \not \equiv 0 \ \ \pmod p. \end{align*} $$
$$ \begin{align*}\binom{m+\frac{q-1}{d}}{m+1} \not \equiv 0 \ \ \pmod p. \end{align*} $$
Note that
![]() $\alpha _p \in (p^r, p^{r+1})$
. Write
$\alpha _p \in (p^r, p^{r+1})$
. Write
![]() $\alpha _p=m+1=(c_r, c_{r-1}, \ldots , c_0)_p$
in its base-p representation. Then, Kummer’s theorem implies that
$\alpha _p=m+1=(c_r, c_{r-1}, \ldots , c_0)_p$
in its base-p representation. Then, Kummer’s theorem implies that
![]() $c_j \leq \frac {(d-1)(p-1)}{d}$
for
$c_j \leq \frac {(d-1)(p-1)}{d}$
for
![]() $j \geq 1$
and
$j \geq 1$
and
![]() $c_0 \leq \frac {(d-1)(p-1)}{d}+1$
. Note that
$c_0 \leq \frac {(d-1)(p-1)}{d}+1$
. Note that
![]() $c_j=\lfloor p\{\alpha _p/p^{j+1}\} \rfloor $
for
$c_j=\lfloor p\{\alpha _p/p^{j+1}\} \rfloor $
for
![]() $0 \leq j \leq r$
, where
$0 \leq j \leq r$
, where
![]() $\{x\}$
denotes the fractional part of a real number x. Indeed, in view of the base-p representation of
$\{x\}$
denotes the fractional part of a real number x. Indeed, in view of the base-p representation of
![]() $\alpha _p$
, we have
$\alpha _p$
, we have
 $$ \begin{align*}c_jp^j+\sum_{i=j+1}^r c_ip^i\leq \alpha_p <(c_j+1)p^j+\sum_{i=j+1}^r c_ip^i,\end{align*} $$
$$ \begin{align*}c_jp^j+\sum_{i=j+1}^r c_ip^i\leq \alpha_p <(c_j+1)p^j+\sum_{i=j+1}^r c_ip^i,\end{align*} $$
thus
![]() $c_j/p\leq \{\alpha _p/p^{j+1}\}<(c_j+1)/p$
, equivalently,
$c_j/p\leq \{\alpha _p/p^{j+1}\}<(c_j+1)/p$
, equivalently,
![]() $c_j=\lfloor p\{\alpha _p/p^{j+1}\} \rfloor $
.
$c_j=\lfloor p\{\alpha _p/p^{j+1}\} \rfloor $
.
The above discussion shows that
![]() $\mathcal {B}_d \subset \mathcal {C}_d \cup \mathcal {D}_d$
, where
$\mathcal {B}_d \subset \mathcal {C}_d \cup \mathcal {D}_d$
, where
 $$ \begin{align*}\mathcal{C}_d= \bigg\{p \in \mathcal{P}_d: p^{2r+1}=\frac{dk(k-1)}{2}+1 \text{ for some positive integer } k\bigg\} \end{align*} $$
$$ \begin{align*}\mathcal{C}_d= \bigg\{p \in \mathcal{P}_d: p^{2r+1}=\frac{dk(k-1)}{2}+1 \text{ for some positive integer } k\bigg\} \end{align*} $$
and
 $$ \begin{align*} \mathcal{D}_d= &\bigg\{p \in \mathcal{P}_d: \sqrt{\frac{q-1}{2d}} \in \bigg[\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1\bigg\} \bigcap \\ &\qquad\qquad\qquad\bigcap_{j=1}^{r} \bigg\{p \in \mathcal{P}_d: \frac{\alpha_p}{p^{j}} \in \bigg [0,\frac{(d-1)(p-1)}{dp}+\frac{2}{p}\bigg) \ \ \pmod 1 \bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{D}_d= &\bigg\{p \in \mathcal{P}_d: \sqrt{\frac{q-1}{2d}} \in \bigg[\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1\bigg\} \bigcap \\ &\qquad\qquad\qquad\bigcap_{j=1}^{r} \bigg\{p \in \mathcal{P}_d: \frac{\alpha_p}{p^{j}} \in \bigg [0,\frac{(d-1)(p-1)}{dp}+\frac{2}{p}\bigg) \ \ \pmod 1 \bigg\}. \end{align*} $$
In view of the prime number theorem for aritheoremetic progressions and Corollary 1.5, it is clear that the relative density of
![]() $\mathcal {C}_d \subset \mathcal {P}_d$
is
$\mathcal {C}_d \subset \mathcal {P}_d$
is
![]() $0$
. Note that as
$0$
. Note that as
![]() $p \to \infty $
,
$p \to \infty $
,
 $$ \begin{align} \alpha_p=\sqrt{\frac{q}{2d}}+o(1)=\frac{p^{r+1/2}}{\sqrt{2d}}+o(1), \quad \frac{(d-1)(p-1)}{dp}+\frac{2}{p}=\frac{d-1}{d}+o(1). \end{align} $$
$$ \begin{align} \alpha_p=\sqrt{\frac{q}{2d}}+o(1)=\frac{p^{r+1/2}}{\sqrt{2d}}+o(1), \quad \frac{(d-1)(p-1)}{dp}+\frac{2}{p}=\frac{d-1}{d}+o(1). \end{align} $$
Thus, in view of Lemma 4.5, it is easy to verify that the relative upper density of
![]() $\mathcal {B}_d \subset \mathcal {P}_d$
is at most the relative upper density of
$\mathcal {B}_d \subset \mathcal {P}_d$
is at most the relative upper density of
![]() $\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
, where
$\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
, where
![]() $\widetilde {\mathcal {D}_d}$
is essentially obtained by dropping the
$\widetilde {\mathcal {D}_d}$
is essentially obtained by dropping the
![]() $o(1)$
error terms from Equation (4.13). More precisely,
$o(1)$
error terms from Equation (4.13). More precisely,
 $$ \begin{align*} \widetilde{\mathcal{D}_d}=\bigg\{p \in \mathcal{P}_d: &\frac{p^{r+1/2}}{\sqrt{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1, \\ &\frac{p^{j+1/2}}{\sqrt{2d}} \in \bigg(0,\frac{d-1}{d}\bigg) \ \ \pmod 1 \text{ for each } 0 \leq j \leq r-1 \bigg\}. \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{D}_d}=\bigg\{p \in \mathcal{P}_d: &\frac{p^{r+1/2}}{\sqrt{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1, \\ &\frac{p^{j+1/2}}{\sqrt{2d}} \in \bigg(0,\frac{d-1}{d}\bigg) \ \ \pmod 1 \text{ for each } 0 \leq j \leq r-1 \bigg\}. \end{align*} $$
Lemma 4.5 then implies that the relative density of
![]() $\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
is
$\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
is
![]() $\frac {1}{4} \cdot (\frac {d-1}{d})^r$
, as desired.
$\frac {1}{4} \cdot (\frac {d-1}{d})^r$
, as desired.
Finally, we consider the case where s is even. In this case,
![]() $s=2r+2$
. Using an almost identical argument, we can show that the relative upper density of
$s=2r+2$
. Using an almost identical argument, we can show that the relative upper density of
![]() $\mathcal {B}_d \subset \mathcal {P}_d$
is at most the relative upper density of
$\mathcal {B}_d \subset \mathcal {P}_d$
is at most the relative upper density of
![]() $\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
, where
$\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
, where
 $$ \begin{align*} \widetilde{\mathcal{D}_d}=\bigg\{p \in \mathcal{P}_d: &\frac{p^{r+1}}{\sqrt{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1, \\ &\frac{p^{j}}{\sqrt{2d}} \in \bigg(0,\frac{d-1}{d}\bigg) \ \ \pmod 1 \text{ for each } 1 \leq j \leq r \bigg\}. \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{D}_d}=\bigg\{p \in \mathcal{P}_d: &\frac{p^{r+1}}{\sqrt{2d}} \in \bigg(\frac{1}{2},\frac{3}{4}\bigg) \ \ \pmod 1, \\ &\frac{p^{j}}{\sqrt{2d}} \in \bigg(0,\frac{d-1}{d}\bigg) \ \ \pmod 1 \text{ for each } 1 \leq j \leq r \bigg\}. \end{align*} $$
Since
![]() $2d$
is not a perfect square, it follows that
$2d$
is not a perfect square, it follows that
![]() $\sqrt {2d}$
is not rational, and thus Lemma 4.5 implies that the relative density of
$\sqrt {2d}$
is not rational, and thus Lemma 4.5 implies that the relative density of
![]() $\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
is
$\widetilde {\mathcal {D}_d} \subset \mathcal {P}_d$
is
![]() $\frac {1}{4} \cdot (\frac {d-1}{d})^r$
, as desired.
$\frac {1}{4} \cdot (\frac {d-1}{d})^r$
, as desired.
5 Applications to the question of Erdős and Moser
First, we recall Gallagher’s larger sieve [Reference Gallagher11].
Lemma 5.1 Let N be a natural number and
![]() $A\subset \{1,2,\ldots , N\}$
. Let
$A\subset \{1,2,\ldots , N\}$
. Let
![]() ${\mathcal P}$
be a set of primes. For each prime
${\mathcal P}$
be a set of primes. For each prime
![]() $p \in {\mathcal P}$
, let
$p \in {\mathcal P}$
, let
![]() $A_p=A \ \pmod {p}$
. For any
$A_p=A \ \pmod {p}$
. For any
![]() $1<Q\leq N$
, we have
$1<Q\leq N$
, we have
 $$ \begin{align*}|A|\leq \frac{\underset{p\leq Q, p\in \mathcal{P}}\sum\log p - \log N}{\underset{p\leq Q, p \in \mathcal{P}}\sum\frac{\log p}{|A_p|}-\log N}, \end{align*} $$
$$ \begin{align*}|A|\leq \frac{\underset{p\leq Q, p\in \mathcal{P}}\sum\log p - \log N}{\underset{p\leq Q, p \in \mathcal{P}}\sum\frac{\log p}{|A_p|}-\log N}, \end{align*} $$
provided that the denominator is positive.
We conclude the paper with the proof of Theorem 1.8.
Proof of Theorem 1.8
Let
![]() $A\subset \{1,2,\ldots , N\}$
such that
$A\subset \{1,2,\ldots , N\}$
such that
![]() $A \hat {+} A$
is contained in the set of d-th powers. To apply the Gallagher sieve inequality, we consider the set of primes
$A \hat {+} A$
is contained in the set of d-th powers. To apply the Gallagher sieve inequality, we consider the set of primes
![]() $\mathcal {P}=\{p: p \equiv 1 \ \pmod d\}.$
For each prime
$\mathcal {P}=\{p: p \equiv 1 \ \pmod d\}.$
For each prime
![]() $p \in \mathcal {P}$
, denote by
$p \in \mathcal {P}$
, denote by
![]() $A_{p}$
the image of
$A_{p}$
the image of
![]() $A \ \pmod {p}$
. For each
$A \ \pmod {p}$
. For each
![]() $p \in \mathcal {P}$
, we can naturally view
$p \in \mathcal {P}$
, we can naturally view
![]() $A_p$
as a subset of
$A_p$
as a subset of
![]() $\mathbb {F}_p$
so that
$\mathbb {F}_p$
so that
![]() $A_p \hat {+} A_p \subset S_d(\mathbb {F}_p) \cup \{0\}$
, and Theorem 1.6 implies that
$A_p \hat {+} A_p \subset S_d(\mathbb {F}_p) \cup \{0\}$
, and Theorem 1.6 implies that
Set
![]() $Q=\frac {2}{d}(\phi (d)\log N)^2$
. By the prime number theorem and standard partial summation, we have
$Q=\frac {2}{d}(\phi (d)\log N)^2$
. By the prime number theorem and standard partial summation, we have
 $$ \begin{align} \sum_{p \in \mathcal{P},p \le Q}\log p \sim \frac{Q}{\phi(d)}, \quad \sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{\sqrt{p}} \sim \frac{2\sqrt{Q}}{\phi(d)}. \end{align} $$
$$ \begin{align} \sum_{p \in \mathcal{P},p \le Q}\log p \sim \frac{Q}{\phi(d)}, \quad \sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{\sqrt{p}} \sim \frac{2\sqrt{Q}}{\phi(d)}. \end{align} $$
Thus, applying Lemma 5.1 and combining the above estimates (5.1) and (5.2), we conclude that
 $$ \begin{align*} |A| &\leq \frac{\sum_{p \in \mathcal{P},p \le Q}\log p - \log N}{\sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{|A_{p}|}-\log N} \leq \frac{\frac{(1+o(1))Q}{\phi(d)}- \log N}{(1+o(1))\sqrt{\frac{d}{2}}\cdot \frac{2\sqrt{Q}}{\phi(d)}-\log N}\\ &\leq \frac{\frac{2+o(1)}{d}\phi(d)(\log N)^2}{(2+o(1))\log N-\log N}=\frac{(2+o(1))\phi(d)}{d}\log N.\\[-42pt] \end{align*} $$
$$ \begin{align*} |A| &\leq \frac{\sum_{p \in \mathcal{P},p \le Q}\log p - \log N}{\sum_{p \in \mathcal{P},p \le Q} \frac{\log p}{|A_{p}|}-\log N} \leq \frac{\frac{(1+o(1))Q}{\phi(d)}- \log N}{(1+o(1))\sqrt{\frac{d}{2}}\cdot \frac{2\sqrt{Q}}{\phi(d)}-\log N}\\ &\leq \frac{\frac{2+o(1)}{d}\phi(d)(\log N)^2}{(2+o(1))\log N-\log N}=\frac{(2+o(1))\phi(d)}{d}\log N.\\[-42pt] \end{align*} $$
Acknowledgements
The author thanks Shamil Asgarli, Ritesh Goenka, Seoyoung Kim, Shuxing Li, Greg Martin, Karen Meagher, Venkata Raghu Tej Pantangi, Misha Rudnev, Ilya Shkredov, József Solymosi, Zixiang Xu, and Semin Yoo for inspiring discussions. The author is also grateful to anonymous referees for their valuable comments and suggestions.