Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T06:54:19.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Representing Multipliers of the Fourier Algebra on Non-Commutative Lp Spaces

Published online by Cambridge University Press:  20 November 2018

Matthew Daws
Matthew Daws*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, United Kingdom email: matt.daws@cantab.net
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the multiplier algebra of the Fourier algebra on a locally compact group $G$ can be isometrically represented on a direct sum on non-commutative 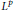${{L}^{p}}$ spaces associated with the right von Neumann algebra of $G$. The resulting image is the idealiser of the image of the Fourier algebra. If these spaces are given their canonical operator space structure, then we get a completely isometric representation of the completely bounded multiplier algebra. We make a careful study of the noncommutative 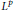${{L}^{p}}$ spaces we construct and show that they are completely isometric to those considered recently by Forrest, Lee, and Samei. We improve a result of theirs about module homomorphisms. We suggest a definition of a Figa-Talamanca–Herz algebra built out of these non-commutative 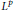${{L}^{p}}$ spaces, say 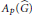${{A}_{p}}(\hat{G})$. It is shown that 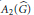${{A}_{2}}(\hat{G})$ is isometric to 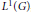${{L}^{1}}(G)$, generalising the abelian situation.

Keywords

43A2243A3046L5122D2542B1546L0746L52multiplierFourier algebranon-commutative Lp spacecomplex interpolation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 4 , 01 August 2011 , pp. 798 - 825
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bergh, J. and Löfström, J., Interpolation spaces. An introduction. Grundlehren der Mathematischen Wissenschaften, 223, Springer-Verlag, Berlin-New York, 1976.Google Scholar
[2] Dales, H. G., Banach algebras and automatic continuity. London Mathematical SocietyMonographs. New Series, 24, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[3] Daws, M., Dual Banach algebras: representations and injectivity. Studia Math. 178(2007), no. 3, 231–275. doi:10.4064/sm178-3-3Google Scholar
[4] De Cannière, J. and Haagerup, U., Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups. Amer. J. Math. 107(1985), no. 2, 455–500. doi:10.2307/2374423Google Scholar
[5] Effros, E. G. and Ruan, Z.-J., Operator spaces. London Mathematical Society Monographs, New Series, 23, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[6] Enock, M. and Schwartz, J.-M., Kac algebras and duality of locally compact groups. Springer-Verlag, Berlin, 1992.Google Scholar
[7] Eymard, P., L’algèbre de Fourier d’un groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.Google Scholar
[8] Forrest, B., Lee, H., and Samei, E., Projectivity of modules over Fourier algebras. Proc. London Math. Soc, to appear. arXiv:0807.4361v2 [math.FA].Google Scholar
[9] Ghahramani, F., Isometric representation of M(G) on B(H). Glasgow Math. J. 23(1982), no. 2, 119–122. doi:10.1017/S0017089500004882Google Scholar
[10] Haagerup, U., Lp-spaces associated with an arbitrary von Neumann algebra. In: Algèbres d’opérateurs et leurs applications en physique mathématique (Proc. Colloq., Marseille, 1977), Colloq. Internat. CNRS, 274, CNRS, Paris, 1979, pp. 175–184.Google Scholar
[11] Haagerup, U., Operator-valued weights in von Neumann algebras. II. J. Funct. Anal. 33(1979), no. 3, 339–361. doi:10.1016/0022-1236(79)90072-7Google Scholar
[12] Herz, C., The theory of p-spaces with an application to convolution operators. Trans. Amer. Math. Soc. 154(1971), 69–82.Google Scholar
[13] Herz, C., Harmonic synthesis for subgroups. Ann. Inst. Fourier (Grenoble) 23(1973), no. 3, 91–123.Google Scholar
[14] Hilsum, M., Les espaces Lp d’une algèbre de von Neumann définies par la derivée spatiale. J. Funct. Anal. 40(1981), no. 2, 151–169. doi:10.1016/0022-1236(81)90065-3Google Scholar
[15] Izumi, H., Constructions of non-commutative Lp-spaces with a complex parameter arising from modular actions. Internat. J. Math. 8(1997), no. 8, 1029–1066. doi:10.1142/S0129167X97000494Google Scholar
[16] Izumi, H., Natural bilinear forms, natural sesquilinear forms and the associated duality on non-commutative Lp-spaces. Internat. J. Math. 9(1998), no. 8, 975–1039. doi:10.1142/S0129167X98000439Google Scholar
[17] Johnson, B. E., An introduction to the theory of centralizers. Proc. London Math. Soc. 14(1964), 299–320. doi:10.1112/plms/s3-14.2.299Google Scholar
[18] Junge, M., Neufang, M., and Ruan, Z.-J., A representation theorem for locally compact quantum groups. Internat. J. Math. 20(2009), no. 3, 377–400. doi:10.1142/S0129167X09005285Google Scholar
[19] Junge, M., Ruan, Z.-J., and Xu, Q., Rigid OLp structures of non-commutative Lp-spaces associated with hyperfinite von Neumann algebras. Math. Scand. 96(2005), no. 1, 63–95.Google Scholar
[20] Kosaki, H., Applications of the complex interpolation method to a von Neumann algebra: noncommutative Lp-spaces. J. Funct. Anal. 56(1984), no. 1, 29–78. doi:10.1016/0022-1236(84)90025-9Google Scholar
[21] Kraus, J. and Ruan, Z.-J., Multipliers of Kac algebras. Internat. J. Math. 8(1997), no. 2, 213–248. doi:10.1142/S0129167X9700010XGoogle Scholar
[22] Kustermans, J. and Vaes, S., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), no. 1, 68–92.Google Scholar
[23] Kustermans, J., Locally compact quantum groups. In: Quantum independent increment processes. I, Lecture Notes in Math., 1865, Springer, Berlin, 2005, pp. 99–180.Google Scholar
[24] Neufang, M., Ruan, Z.-J., and Spronk, N., Completely isometric representations of McbA(G) and UCB(bG). Trans. Amer. Math. Soc. 360(2008), no. 3, 1133–1161. doi:10.1090/S0002-9947-07-03940-2Google Scholar
[25] Palmer, T.W., Banach algebras and the general theory of ¤-algebras, Vol. 1. Algebras and Banach algebras. Encyclopedia of Mathematics and its Applications, 49, Cambridge University Press, Cambridge, 1994.Google Scholar
[26] Pisier, G., The operator Hilbert space OH, complex interpolation and tensor norms. Mem. Amer. Math. Soc. 122(1996), no. 585.Google Scholar
[27] Pisier, G., Non-commutative vector valued Lp-spaces and completely p-summing maps. Astérisque 247(1998).Google Scholar
[28] Pisier, G., Introduction to operator space theory. London Mathematical Society Lecture Note Series, 294, Cambridge University Press, Cambridge, 2003.Google Scholar
[29] Pisier, G. and Xu, Q., Non-commutative Lp-spaces. In: Handbook of the geometry of Banach spaces, Vol. 2, North-Holland, Amsterdam, 2003, pp. 1459–1517.Google Scholar
[30] Runde, V., Operator Figà-Talamanca–Herz algebras. Studia Math. 155(2003), no. 2, 153–170. doi:10.4064/sm155-2-5Google Scholar
[31] Spronk, N., Measurable Schur multipliers and completely bounded multipliers of the Fourier algebras. Proc. London Math. Soc. 89(2004), no. 1, 161–192. doi:10.1112/S0024611504014650Google Scholar
[32] Stafney, J. D., The spectrum of an operator on an interpolation space. Trans. Amer. Math. Soc. 144(1969), 333–349. doi:10.1090/S0002-9947-1969-0253054-7Google Scholar
[33] Stratila, S. and Zsodó, L., Lectures on von Neumann algebras. Revision of the 1975 original, Translated from the Romanian by Silviu Teleman, Abacus Press, Tunbridge Wells, 1979.Google Scholar
[34] Takesaki, M., Theory of operator algebras. II. Encyclopaedia of Mathematical Sciences, 125, Operator Algebras and Non-commutative Geometry, 6, Springer-Verlag, Berlin, 2003.Google Scholar
[35] Terp, M., Interpolation spaces between a von Neumann algebra and its predual. J. Operator Theory 8(1982), no. 2, 327–360.Google Scholar
[36] Uygul, F., A representation theorem for completely contractive dual Banach algebras. J. Operator Theory 62(2009), no. 2, 237–340.Google Scholar
[37] Wendel, J. G., Left centralizers and isomorphisms of group algebras. Pacific J. Math. 2(1952), 251–261.Google Scholar
[38] Xu, Q., Interpolation of operator spaces. J. Funct. Anal. 139(1996), no. 2, 500–539. doi:10.1006/jfan.1996.0094Google Scholar
[39] Young, N. J., Periodicity of functionals and representations of normed algebras on reflexive spaces. Proc. Edinburgh Math. Soc. 20(1976/77), no. 2, 99–120. doi:10.1017/S0013091500010610Google Scholar