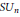Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-06T10:46:02.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Reducibility for $S{{U}_{n}}$ and Generic Elliptic Representations

Published online by Cambridge University Press:  20 November 2018

David Goldberg
David Goldberg*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, U.S.A. e-mail: goldberg@math.purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study reducibility of representations parabolically induced from discrete series representations of 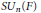$S{{U}_{n}}(F)$ for 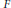$F$ a $p$-adic field of characteristic zero. We use the approach of studying the relation between $R$-groups when a reductive subgroup of a quasi-split group and the full group have the same derived group. We use restriction to show the quotient of $R$-groups is in natural bijection with a group of characters. Applying this to 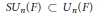$S{{U}_{n}}(F)\,\subset \,{{U}_{n}}(F)$ we show the $R$ group for 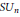$S{{U}_{n}}$ is the semidirect product of an $R$-group for 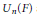${{U}_{n}}(F)$ and this group of characters. We derive results on nonabelian $R$-groups and generic elliptic representations as well.

Keywords

22E5022E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 2 , 01 April 2006 , pp. 344 - 361
Copyright
Copyright © Canadian Mathematical Society 2006

References

[A1] Arthur, J., Unipotent automorphic representations: conjectures. Soc. Math. France, Asterisque 171-172, 1989, pp. 13–17.Google Scholar
[A2] Arthur, J., On elliptic tempered characters. Acta. Math. 171(1993), 73–138.Google Scholar
[B] Borel, A., Automorphic L-functions. Proc. Sympos. Pure Math. 33, American Mathematical Society, Providence, RI, 1979, pp. 27–61.Google Scholar
[G-K] Gelbart, S. S. and Knapp, A. W., L-indistinguishability and R-groups for the special linear group. Adv. in Math. 43(1982), 101–121.Google Scholar
[G1] Goldberg, D., R-groups and elliptic representations for SLn . Pacific J. Math 165(1994), 77–92.Google Scholar
[G2] Goldberg, D., R-groups and elliptic representations for unitary groups. Proc. Amer.Math. Soc. 123(1995), 1267–1276.Google Scholar
[G3] Goldberg, D., Some results on reducibility for unitary groups and local Asai L-functions. J. reine angew. Math 448(1994), 65–95.Google Scholar
[G4] Goldberg, D., R-groups and elliptic representations for similitude groups. Math. Annalen 307(1997), 569–588.Google Scholar
[G-S] Goldberg, D. and Shahidi, F., The tempered spectrum of quasi-split classical groups. II. Canad. J. Math. 53(2001), no. 2, 244–277.Google Scholar
[H-C] Harish-Chandra, , Harmonic analysis on reductive p-adic groups. Proc. Sympos. Pure Math. 26, Providence, RI, 1973, pp. 167–192.Google Scholar
[H] Henniart, G., Correspondance de Langlands et fonctions L des carrés extérieur et symétrique. preprint IHES.Google Scholar
[Hr] Herb, R. A., Elliptic representations of Sp(2n . and SO(n). Pacific J. Math. 161(1993), 347–358.Google Scholar
[K1] Keys, C. D., Principal series representations of special unitary groups over local fields. Compo. Math. 51(1984), 115–130.Google Scholar
[K2] Keys, C. D., L-indistinguishability and R-groups for quasi-split unitary groups in even dimension. Ann. Sci. Ec. Norm. Sup. 20(1987), 31–64.Google Scholar
[L] Langlands, R. P., Representations of abelian algebraic groups. Yale University, 1968.Google Scholar
[P] Prasad, D., Theta correspondence for unitary groups. Pacific J. Math 194(2000), 427–438.Google Scholar
[Se] Serre, J.-P. Linear Representations of Finite Groups. Springer-Verlag, New York, 1977.Google Scholar
[Sh1] Shahidi, F., Twisted endoscopy and reducibility of induced representations for p-adic groups. Duke J. Math. 66(1992), 1–41.Google Scholar
[Sh2] Shahidi, F., A proof of Langlands conjecture for Plancherel measures; complementary series for p-adic groups. Ann. Math. (2) 132(1990), 273–330.Google Scholar
[Sh3] Shahidi, F., Some results on L-indistinguishability for SL(r). Canad. J. Math 35(1983), 1075–1109.Google Scholar
[Si1] Shahidi, F., The Knapp-Stein dimension theorem for p-adic groups. Proc. Amer.Math. Soc. 68(1978), 243–246.Google Scholar
[Si2] Silberger, A. J. The Knapp-Stein dimension theorem for p-adic groups. Correction. Proc. Amer. Math. Soc. 76(1979), 169–170.Google Scholar
[T] Tadic, M., Notes on representations of non-archimedean SL(n). Pacific J.Math. 152(1992), 375–396.Google Scholar