Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T09:50:16.137Z Has data issue: false hasContentIssue false
  • English
  • Français

Radical Ideals in Valuation Domains

Published online by Cambridge University Press:  20 November 2018

John E. van den Berg
John E. van den Berg*
Affiliation:
School of Mathematical Sciences, University of KwaZulu-Natal Pietermaritzburg, Private Bag X01, Scottsville 3209, South Africa email: vandenberg@ukzn.ac.za
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An ideal $I$ of a ring $R$ is called a radical ideal if 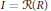$I\,=\,\mathcal{R}(R)$ where 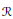$\mathcal{R}$ is a radical in the sense of Kurosh–Amitsur. The main theorem of this paper asserts that if $R$ is a valuation domain, then a proper ideal $I$ of $R$ is a radical ideal if and only if $I$ is a distinguished ideal of $R$ (the latter property means that if $J$ and 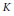$K$ are ideals of $R$ such that 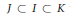$J\,\subset \,I\,\subset \,K$ then we cannot have 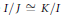$I/J\,\cong \,K/I$ as rings) and that such an ideal is necessarily prime. Examples are exhibited which show that, unlike prime ideals, distinguished ideals are not characterizable in terms of a property of the underlying value group of the valuation domain.

Keywords

16N8013A18
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 4 , 01 August 2007 , pp. 880 - 896
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Andrunakievič, V. A., Radicals of associative rings. I. Amer. Math. Soc. Translations 52(1966), 95–128.Google Scholar
[2] Andruszkiewicz, R. R. and Puczyłowski, E. R., Accessible subrings and Kurosh's chains of associative rings. Algebra Colloq. 4(1997), no. 1, 79–88.Google Scholar
[3] Divinsky, N. J., Rings and Radicals. Mathematical Expositions 14, University of Toronto Press, Toronto, 1965.Google Scholar
[4] Fuchs, L., Partially Ordered Algebraic Systems. Pergamon Press, Oxford, 1963.Google Scholar
[5] Fuchs, L. and Salce, L., Modules over Valuation Domains. Lecture Notes in Pure and Applied Mathematics Series 97, Marcel Dekker, New York, 1985.Google Scholar
[6] Gardner, B. J. and Wiegandt, R., Radical Theory of Rings. Monographs and Textbooks in Pure and Applied Mathematics 261, Marcel Dekker, New York, 2003.Google Scholar
[7] Hungerford, T. W., Algebra. Graduate Texts in Mathematics Series 73, Springer-Verlag, New York, 1980.Google Scholar
[8] McConnell, N. R., Radical ideals of Dedekind domains and their extensions. Comm. Algebra 19(1991), no. 2, 559–583.Google Scholar
[9] Propes, R. E., Radicals of PID's and Dedekind domains. Canad. J. Math. 24(1972), no. 4, 566–572.Google Scholar
[10] Puczyłowski, E. R., Radicals of rings. Comm. Algebra 22(1994), no. 13, 5419–5436.Google Scholar
[11] Ribenboim, P., Théorie des valuations. Second edition. Les Presses de l’Université de Montréal Press, Montréal, 1968.Google Scholar
[12] Zariski, O. and Samuel, P., Commutative Algebra. Vol. II, D. Van Nostrand, Princeton, NJ, 1960.Google Scholar