Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T08:54:16.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbation and Solvability of Initial Lp Dirichlet Problems for Parabolic Equations over Non-cylindrical Domains

Published online by Cambridge University Press:  20 November 2018

Jorge Rivera-Noriega
Jorge Rivera-Noriega*
Affiliation:
Facultad de Ciencias, Universidad Autónoma del Estado de Morelos, Av. Universidad 1001, Col Chamilpa, Cuernavaca Mor CP 62209, México. e-mail: rnoriega@uaem.mx
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For parabolic linear operators $L$ of second order in divergence form, we prove that the solvability of initial 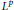${{L}^{p}}$ Dirichlet problems for the whole range 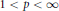$1\,<\,p\,<\,\infty $ is preserved under appropriate small perturbations of the coefficients of the operators involved. We also prove that if the coefficients of $L$ satisfy a suitable controlled oscillation in the form of Carleson measure conditions, then for certain values of 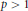$p\,>\,1$, the initial 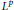${{L}^{p}}$ Dirichlet problem associated with 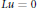$Lu\,=\,0$ over non-cylindrical domains is solvable. The results are adequate adaptations of the corresponding results for elliptic equations.

Keywords

35K20Initial Lp Dirichlet problemsecond order parabolic equations in divergence formnoncylindrical domainsreverse Hölder inequalities
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 2 , 01 April 2014 , pp. 429 - 452
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Argiolas, R. and Grimaldi, A. P., The Dirichlet problem for second order parabolic operators in non-cylindrical domains. Math. Nachr. 283(2010), no. 4, 522–543. http://dx.doi.org/10.1002/mana.200610815 Google Scholar
[2] Bramanti, M. and Cerutti, M. C.,W1;2 p solvability for the Cauchy-Dirichlet problem for parabolic equations with VMO coefficients. Comm. Partial Differential Equations 18(1993), no. 9–10, 1735–1763. http://dx.doi.org/10.1080/03605309308820991 Google Scholar
[3] Brown, R. M., Area integral estimates for caloric functions. Trans. Amer. Math. Soc. 315(1989), no. 2, 565–589. http://dx.doi.org/10.1090/S0002-9947-1989-0994163-7 Google Scholar
[4] Calderón, A. P. and Torchinsky, A., Parabolic maximal functions associated with a distribution. Advances in Math. 16(1975), 1–64. http://dx.doi.org/10.1016/0001-8708(75)90099-7 Google Scholar
[5] Dindos, M., Petermichl, S., and Pipher, J., The Lp dirichlet problem for second order elliptic operators and a p-adapted square function. J. Funct. Anal. 249(2007), no. 2, 372–392. http://dx.doi.org/10.1016/j.jfa.2006.11.012 Google Scholar
[6] Dindos, M. and Wall, T., The Lp Dirichlet problem for second order, non-divergence form operators: solvability and perturbation results. J. Funct. Anal. 261(2011), no. 7, 1753–1774. http://dx.doi.org/10.1016/j.jfa.2011.05.013 Google Scholar
[7] Eklund, N., Generalized parabolic functions using the Perron-Wiener-Brelot method. Proc. Amer. Math. Soc. 74(1979), no. 1, 247–253. http://dx.doi.org/10.1090/S0002-9939-1979-0524295-8 Google Scholar
[8] Escauriaza, L., Weak type-(1,1) inequalities and regularity properties of adjoint and normalized adjoint solutions to linear nondivergence form operators with VMO coefficients. Duke Math. J. 74(1994), no. 1, 177–201. http://dx.doi.org/10.1215/S0012-7094-94-07409-7 Google Scholar
[9] Escauriaza, L., The Lp Dirichlet problem for small perturbations of the Laplacian. Israel J. Math. 94(1996), 353–366. http://dx.doi.org/10.1007/BF02762711 Google Scholar
[10] Fabes, E. B., Singular integrals and partial differential equations of parabolic type. Studia Math. 28(1966/1967), 81–131.Google Scholar
[11] Fabes, E. B., Garofalo, N., and Salsa, S., A backward Harnack inequality and Fatou theorem for non-negative solutions of parabolic equations. Illinois J. Math. 30(1986), no. 4, 536–565.Google Scholar
[12] Fabes, E. B. and Rivière, N. M., Singular integrals with mixed homogeneity. Studia Math. 27(1966), 19–38.Google Scholar
[13] Fabes, E. B. and Safonov, M. V., Behavior near the boundary of positive solutions of second order parabolic equations. Proceedings of the conference dedicated to Professor Miguel de Guzmán (El Escorial, 1996), J. Fourier Anal. Appl. 3(1997), Special Issue, 871–882. http://dx.doi.org/10.1007/BF02656492 Google Scholar
[14] Fabes, E. B., Safonov, M. V., and Yuan, Y., Behavior near the boundary of positive solutions of second order parabolic equations. II. Trans. Amer. Math. Soc. 351(1999), no. 12, 4947–4961. http://dx.doi.org/10.1090/S0002-9947-99-02487-3 Google Scholar
[15] Hofmann, S., Parabolic singular integrals of Calderén-type, rough operators, and caloric layer potentials. Duke Math. J. 90(1997), no. 2, 209–259. http://dx.doi.org/10.1215/S0012-7094-97-09008-6 Google Scholar
[16] Hofmann, S. and Lewis, J. L., L2 solvability and representation by caloric layer potentials in time varying domains. Ann. of Math. 144(1996), no. 2, 349–420. http://dx.doi.org/10.2307/2118595 Google Scholar
[17] Hofmann, S., The Dirichlet problem for parabolic operators with singular drift terms. Mem. Amer. Math. Soc. 151(2001), no. 719.Google Scholar
[18] Hofmann, S., The Lp-Neumann problem for the heat equation in non-cylindrical domains. J. Funct. Anal. 220(2005), no. 1, 1–54. http://dx.doi.org/10.1016/j.jfa.2004.10.016 Google Scholar
[19] Hofmann, S., Lewis, J. L., and Nyström, K., Existence of big pieces of graphs for parabolic problems. Ann. Acad. Sci. Fenn. Math. 28(2003), no. 2, 355–384.Google Scholar
[20] Kenig, C. E., Koch, H., Pipher, J., and Toro, T., A new approach to absolute continuity of elliptic measure with applications to non-symmetric equations. Adv. Math. 153(2000), no. 2, 231–298. http://dx.doi.org/10.1006/aima.1999.1899 Google Scholar
[21] Kenig, C. E. and Pipher, J., The Dirichlet problem for elliptic equations with drift terms. Publ. Mat 45(2001), no. 1, 199–217.Google Scholar
[22] Lewis, J. L. and Murray, M. A. M., The method of layer potentials for the heat equation in time-varying domains. Mem. Amer. Math. Soc. 114(1995), no. 545.Google Scholar
[23] Lewis, J. L. and Silver, J., Parabolic measure and the Dirichlet problem for the heat equation in two dimensions. Indiana Univ. Math. J. 37(1988), no. 4, 801–839. http://dx.doi.org/10.1512/iumj.1988.37.37039 Google Scholar
[24] Nyström, K., The Dirichlet problem for second order parabolic operators. Indiana Univ. Math. J. 46(1997), no. 1, 183–245.Google Scholar
[25] Rivera-Noriega, J., Absolute continuity of parabolic measure and area integral estimates in non-cylindrical domains. Indiana Univ. Math. J. 52(2003), no. 2, 477–525.Google Scholar
[26] Rivera-Noriega, J., A parabolic version of Corona decompositions. Illinois J. Math. 53(2009), no. 2, 533–559.Google Scholar
[27] Safonov, M. V. and Yuan, Y., Doubling properties for second order parabolic equations. Ann. of Math. 150(1999), no. 1, 313–327. http://dx.doi.org/10.2307/121104 Google Scholar
[28] Sarason, D., Functions of vanishing mean oscillation. Trans. Amer. Math. Soc. 207(1975), 391–405. http://dx.doi.org/10.1090/S0002-9947-1975-0377518-3 Google Scholar
[29] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43. Monographs in Harmonic Analysis, III, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[30] Strichartz, R. S., Bounded mean oscillation and Sobolev spaces. Indiana Univ. Math. J. 29(1980), no. 4, 539–558. http://dx.doi.org/10.1512/iumj.1980.29.29041 Google Scholar