Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T05:52:52.658Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Commutators of Singular Integral Operators with Rough Convolution Kernels

Published online by Cambridge University Press:  20 November 2018

Xiaoli Guo  and
Guoen Hu
Xiaoli Guo
Affiliation:
Department of Mathematics and Information Science, Zhengzhou University of Light Industry, Zhengzhou 450002, P.R., China e-mail: xlguo@zzuli.edu.cn
Guoen Hu
Affiliation:
Department of Applied Mathematics, Zhengzhou Information Science and Technology Institute, Zhengzhou 450001, P. R., China e-mail: huguoen@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 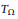${{T}_{\Omega }}$ be the singular integral operator with kernel 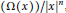$\left( \Omega \left( x \right) \right)/{{\left| x \right|}^{n}}$, where 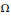$\Omega $ is homogeneous of degree zero, has mean value zero, and belongs to 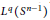${{L}^{q}}\left( {{S}^{n-1}} \right)$ for some 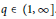$q\,\in \,\left( 1,\,\infty \right]$. In this paper, the authors establish the compactness on weighted 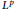${{L}^{p}}$ spaces and the Morrey spaces, for the commutator generated by 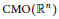$\text{CMO}\left( {{\mathbb{R}}^{n}} \right)$ function and 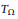${{T}_{\Omega }}$. The associated maximal operator and the discrete maximal operator are also considered.

Keywords

42B2047B07commutatorsingular integral operatorcompact operatorcompletely continuous operatormaximal operatorMorrey space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 4 , 01 August 2016 , pp. 816 - 840
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Adams, D. R. and Xiao, J., Morrey potential and harmonic analysis. Ark. Mat. 50(2012), no. 2,201–230 http://dx.doi.Org/10.1007/s11512-010-0134-0 Google Scholar
[2] Alvarez, J., Bagby, R. J., Kurtz, D. S., and Perez, C., Weighted estimates for commutators of linear operators. Studia Math. 104(1993), no. 2,195–209.Google Scholar
[3] Benyi, A., Damian, W., Moen, K., and Torres, R. H., Compact bilinear commutator: the weighted case. Michigan Math. J. 64(2015), no. 1, 39–51.http://dx.doi.org/10.1307/mmjV1427203284 Google Scholar
[4] Bourdaud, G., Lanze de Cristoforis, M., and Sickel, W., Functional calculus on BMO and related spaces. J. Funct. Anal. 189(2002), 515–538.http://dx.doi.Org/10.1OO6/jfan.2OO1.3847 Google Scholar
[5] Calderon, A. P. and Zygmund, A., On the existence of certain singular integrals. Acta Math. 88(1952), 85–139.http://dx.doi.org/10.1007/BF02392130 Google Scholar
[6] Calderon, A. P. ,On singular integrals. Amer. J. Math. 78(1956), 289–309.http://dx.doi.Org/10.2307/2372517 Google Scholar
[7] Capri, O. N. and Segovia, C., Behavior of Lr-Dini singular integrals in weighted L1 spaces.Studia Math. 92(1989), 21–36.Google Scholar
[8] Chen, J. and Hu, G., Compact commutators of rough singular integral operators. Canada Math.Bull.. 58(2015), no. 1, 19–29.http://dx.doi.org/10.4153/CMB-2014-042-1 Google Scholar
[9]. Chen, Y., Ding, Y., and Wang, X., Compactness of commutators for singular integrals on Morrey spaces. Canad. J. Math. 64(2012), no. 2, 257–281.http://dx.doi.Org/10.4153/CJM-2O11-043-1 Google Scholar
[10] Clop, A. and Cruz, V., Weighted estimates for Beltrami equations. Ann. Acad. Sci. Fenn. Math. 38(2013), no. 1,91–113.http://dx.doi.org/10.5186/aasfm.2013.3818 Google Scholar
[11] Coifman, R. R., Rochberg, R., and Weiss, G., Factorizaton theorems for Hardy spaces in several variables. Ann. Math. 103(1976), no. 3, 611–635.http://dx.doi.Org/10.2307/1970954 Google Scholar
[12] Coifman, R. R. and Weiss, G., Extension of Hardy spaces and their use in analysis. Bull. Amer.Math. Soc. 83(1977),569–645.http://dx.doi.org/10.1090/S0002-9904-1977-14325-5 Google Scholar
[13] Connett, W., Singular integrals near Ll. In: Harmonic analysis in Euclidean spaces, Proc. Sympos. Pure Math., 35, American Mathematical Society, Providence, RI, 1979, pp. 163–165.Google Scholar
[14] Fan, D. and Pan, Y., Singular integral operators with rough kernels supported by subvarieties. Amer.J. Math. 119(1997), no. 4, 799–839.http://dx.doi.Org/10.1353/ajm.1997.0024 Google Scholar
[15] Duoandikoetxea, J., Weighted norm inequalities for homogeneous singular integrals. Trans. Amer.Math. Soc. 336(1993), no. 2, 869–880.http://dx.doi.org/10.1090/S0002-9947-1993-1089418-5 Google Scholar
[16] Duoandikoetxea, J. and Rubio de Francia, J. L., Maximal and singular integrals via Fourier transform estimates. Invent. Math. 84(1986), no. 3, 541–561.http://dx.doi.Org/10.1007/BF01388746 Google Scholar
[17] Grafakos, L., Modern Fourier analysis. Second éd., Graduate Texts in Mathematics, 250, Springer, New York, 2008.Google Scholar
[18] Grafakos, L. and Stefanov, A., Lp bounds for singular integrals and maximal singular integrals with rough kernels. Indiana Univ. Math. J. 47(1998), no. 2, 455–469.Google Scholar
[19] Hu, G., Weighted norm inequalities for the commutators of homogeneous singular integral operators. Acta Math. Sinica New Ser. 11(1995), Special Issue, 77–88.Google Scholar
[20] Hu, G., Lf boundedness for the commutator of a homogeneous singular integral operator. Studia Math. 154(2003), no. 1. 13–27.http://dx.doi.org/10.4064/sm154-1-2 Google Scholar
[21] Kurtz, D. S. and Wheeden, R., Results on weighted norm inequalities for multipliers. Trans. Amer.Math. Soc. 255(1979),343–362.http://dx.doi.org/10.1090/S0002-9947-1979-0542885-8 Google Scholar
[22] Morrey, C., On the solution of quasi-linear elliptic partial differential equation. Trans. Amer. Math.Soc. 43(1938), no. 1, 126–166.http://dx.doi.org/10.1090/S0002-9947-1938-1501936-8 Google Scholar
[23] Nakai, E., Hardy-Littlewood maximal operators, singular integral operators and the Rieszpotentials on generalized Morrey spaces. Math. Nachr. 166(1994), 95–103.http://dx.doi.Org/10.1002/mana.19941660108 Google Scholar
[24] Ricci, F. and Weiss, G., A characterization ofH1(S“∼1). In: Harmonic analysis in Euclidean spaces Part 1, Proc. Sympos. Pure Math., 35, American Mathematical Society, Providence, RI, 1979, pp. 289–294.Google Scholar
[25] Ruiz, A. and Vega, L.,Unique continuation for Schrodinger operators with potential in Morre space. Publ. Mat. 35(1991), no. 1, 291–298. http://dx.doi.Org/10.5565/PUBLMAT_35191_15 Google Scholar
[26] Seeger, A., Singular integral operators with rough convolution kernels. J. Amer. Math. Soc. 9(1996),no. 1, 95–105.http://dx.doi.org/10.1090/S0894-0347-96-00185-3 Google Scholar
[27] Shen, Z., Boundary value problems in Morrey spaces for elliptic systems on Lipschitz domains. Amer. J.Math. 125(2003), no. 5, 1079–1115.http://dx.doi.org/10.1353/ajm.2003.0035 Google Scholar
[28] Stein, E. M. and Weiss, G., Interpolation of operators with changes of measures. Trans. Amer. Math.Soc. 87(1958), 159–172.http://dx.doi.org/10.1090/S0002-9947-1958-0092943-6 Google Scholar
[29] Uchiyama, A., On the compactness of operators ofHankel type. Tohoku Math. J. 30(1978), 163–171.http://dx.doi.org/10.2748/tmjV1178230105 Google Scholar
[30] Watson, D. K., Weighted estimates for singular integrals via Fourier transform estimates.Duke Math. J. 60(1990), no. 2, 389–399.http://dx.doi.org/10.1215/S0012-7094-90-06015-6 Google Scholar