Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-11T08:10:51.807Z Has data issue: false hasContentIssue false
  • English
  • Français

On $\mathcal{C}\mathcal{R}$-Epic Embeddings and Absolute $\mathcal{C}\mathcal{R}$-Epic Spaces

Published online by Cambridge University Press:  20 November 2018

Michael Barr ,
R. Raphael  and
R. G. Woods
Michael Barr
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, QC, H3A 2K6, e-mail: barr@barrs.org
R. Raphael
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montreal, QC, H4B 1R6, e-mail: raphael@alcor.concordia.ca
R. G. Woods
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, MB, R3T 2N2, rgwoods@cc.umanitoba.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study Tychonoff spaces 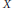$X$ with the property that, for all topological embeddings 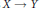$X\,\to \,Y$, the induced map 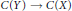$C(Y)\,\to \,C(X)$ is an epimorphism of rings. Such spaces are called absolute $\mathcal{C}\mathcal{R}$-epic. The simplest examples of absolute $\mathcal{C}\mathcal{R}$-epic spaces are $\sigma $-compact locally compact spaces and Lindelöf $P$-spaces. We show that absolute $\mathcal{C}\mathcal{R}$-epic first countable spaces must be locally compact.

However, a “bad” class of absolute $\mathcal{C}\mathcal{R}$-epic spaces is exhibited whose pathology settles, in the negative, a number of open questions. Spaces which are not absolute $\mathcal{C}\mathcal{R}$-epic abound, and some are presented.

Keywords

18A2054C4554B30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1121 - 1138
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Ball, R. N., Comfort, W. W., Garcia-Ferreira, S., Hager, A.W., van Mill, J., and Robertson, L. C., ǫ-spaces. Rocky Mountain J. Math. 25(1995), 867–886.Google Scholar
[2] Ball, R. N. and Hager, A. W., The relative uniform density of the continuous functions in the Baire functions, and of a divisible Archimedean l-group in any epicompletion. Topology Appl. 97(1999), 109–126.Google Scholar
[3] Barr, M., Burgess, W., and Raphael, R., Ring epimorphisms and C(X). Theory Appl. Categ. 11(2003), 283–308.Google Scholar
[4] Blair, R. L. and Hager, A. W., Extensions of zero-sets and real-valued functions. Math. Z. 136(1974), 41–52.Google Scholar
[5] van Douwen, E., Remote points. Dissertationes Math. 188(1981),Warsaw.Google Scholar
[6] van Douwen, E., Applications of maximal topologies. Topology Appl. 51(1993), 125–193.Google Scholar
[7] van Douwen, E., Kunen, K., and van Mill, J., There can be C*-embedded dense proper subspaces in βω − ω. Proc. Amer.Math. Soc. 105(1989), 462–470.Google Scholar
[8] Engelking, R., General topology. Second edition. Sigma Series in Pure Mathematics 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[9] Fine, N. J. and Gillman, L., Extension of continuous functions in βN. Bull. Amer.Math. Soc. 66(1960), 376–381.Google Scholar
[10] Fine, N., Gillman, L., and Lambek, J., Rings of Quotients of Rings of Functions. McGill University Press, Montreal, 1966.Google Scholar
[11] Gillman, L. and Jerison, M., Rings of Continuous Functions. D. Van Nostrand, Princeton, NJ, 1960.Google Scholar
[12] Hager, A.W. and Martinez, J., C-epic compactifications. Topology Appl. 117(2002), 113–138.Google Scholar
[13] Hodel, R., Cardinal functions. In: Handbook of Set Theoretic Topology, (Kunen, I. K. and Vaughan, J. E., eds.), North Holland, Amsterdam, 1984, pp. 1–61.Google Scholar
[14] Isbell, J. R., Epimorphisms and dominions. In: Proc. Conf. Categorical Algebra, Springer-Verlag, New York, 1966, pp. 232–246.Google Scholar
[15] Kruse, A. H., Badly incomplete normed linear spaces. Math. Z. 83(1964), 314–320.Google Scholar
[16] Levy, R., Almost P-spaces. Canad. J. Math. 29(1977), 284–288.Google Scholar
[17] Levy, R., Non-extendability of bounded continuous functions. Canad. J. Math. 32(1980), 867–879.Google Scholar
[18] Levy, R. and Rice, M. D., Normal P-spaces and the Gδ-topology. Colloq. Math. 44(1981), 227–240.Google Scholar
[19] Martinez, J. and McGovern, W. W., When the maximal ring of quotients of C(X) is uniformly complete. Topology Appl. 116(2001), 185–198.Google Scholar
[20] Mazet, P., Générateurs, relations et épimorphismes d’anneaux. C. R. Acad. Sci. Paris Sér A-B 266(1968), A309–A311.Google Scholar
[21] Olivier, J.-P., Anneaux absolument plats universels et épimorphismes. C.R. Acad. Sci. Paris Sér A-B, 266(1968), A317–A318.Google Scholar
[22] Porter, J. R. and Woods, R. G., Extensions and Absolutes of Hausdorff Spaces. Springer-Verlag, New York, 1988.Google Scholar
[23] Schwartz, N., Rings of continuous functions as real closed rings. In: Ordered Algebraic Structures, (Holland, W. C. and Martinez, J., eds.), Kluwer, Dordecht, 1997, pp. 277–313.Google Scholar
[24] Smirnov, Yu. M., On normally placed sets of normal spaces. Mat. Sbornik N.S. 29(1951), 173–176 (Russian).Google Scholar
[25] Storrer, H., Epimorphismen von kommutativen Ringen. Comment.Math. Helv. 43(1968), 378–401.Google Scholar
[26] Woods, R. G., Characterizations of some C*-embedded subspaces of βN. Pacific J. Math. 65(1976), 573–579.Google Scholar