Published online by Cambridge University Press: 20 November 2018
In this paper, we investigate Dirichlet spaces  ${{D}_{\mu }}$ with superharmonic weights induced by positive Borel measures
${{D}_{\mu }}$ with superharmonic weights induced by positive Borel measures 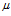 $\mu $
on the open unit disk. We establish the Alexander-Taylor-Ullman inequality for
$\mu $
on the open unit disk. We establish the Alexander-Taylor-Ullman inequality for  ${{D}_{\mu }}$
spaces and we characterize the cases where equality occurs. We define a class of weighted Hardy spaces
${{D}_{\mu }}$
spaces and we characterize the cases where equality occurs. We define a class of weighted Hardy spaces  $H_{\mu }^{2}$ via the balayage of the measure
$H_{\mu }^{2}$ via the balayage of the measure 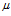 $\mu $
. We show that
$\mu $
. We show that  ${{D}_{\mu }}$
is equal to
${{D}_{\mu }}$
is equal to  $H_{\mu }^{2}$
if and only if
$H_{\mu }^{2}$
if and only if 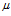 $\mu $
is a Carleson measure for
$\mu $
is a Carleson measure for  ${{D}_{\mu }}$
. As an application, we obtain the reproducing kernel of
${{D}_{\mu }}$
. As an application, we obtain the reproducing kernel of  ${{D}_{\mu }}$
when
${{D}_{\mu }}$
when 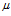 $\mu $ is an infinite sum of point-mass measures. We consider the boundary behavior and innerouter factorization of functions in
$\mu $ is an infinite sum of point-mass measures. We consider the boundary behavior and innerouter factorization of functions in  ${{D}_{\mu }}$. We also characterize the boundedness and compactness of composition operators on
${{D}_{\mu }}$. We also characterize the boundedness and compactness of composition operators on  ${{D}_{\mu }}$.
${{D}_{\mu }}$.