Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T12:50:13.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Nearly Countable Dense Homogeneous Spaces

Published online by Cambridge University Press:  20 November 2018

Michael Hrušák  and
Jan van Mill
Michael Hrušák
Affiliation:
Centro de Ciencas Matemáticas, UNAM, A.P. 61-3, Xangari, Morelia, Michoacán, 58089, México. e-mail: michael@matmor.unam.mx
Jan van Mill
Affiliation:
Faculty of Sciences, Department of Mathematics, VU University Amsterdam, De Boelelaan 1081a , 1081 HV Amsterdam, The Netherlands. e-mail: j.van.mill@vu.nl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study separable metric spaces with few types of countable dense sets. We present a structure theorem for locally compact spaces having precisely $n$ types of countable dense sets: such a space contains a subset 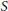$S$ of size at most $n-1$ such that 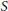$S$ is invariant under all homeomorphisms of 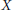$X$ and 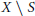$X\,\backslash \,S$ is countable dense homogeneous. We prove that every Borel space having fewer than $\mathfrak{c}$ types of countable dense sets is Polish. The natural question of whether every Polish space has either countably many or $\mathfrak{c}$ many types of countable dense sets is shown to be closely related to Topological Vaught's Conjecture.

Keywords

54H0503E1554E50countable dense homogeneousnearly countable dense homogeneousEffros TheoremVaught's conjecture
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 4 , 01 August 2014 , pp. 743 - 758
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

*

The first author was supported by a PAPIIT grant IN 102311 and CONACyT grant 177758. The second author is pleased to thank the Centro de Ciencas Matemáticas in Morelia for generous hospitality and support.

References

[1] Ancel, F. D., An alternative proof and applications of a theorem of E. G. Effros. Michigan Math. J. 34(1987), no. 1, 39–55. http://dx.doi.org/10.1307/mmj/1029003481 CrossRefGoogle Scholar
[2] Baumgartner, J. E., Partition relations for countable topological spaces. J. Combin. Theory Ser. A. 43(1986), no. 2, 178–195. http://dx.doi.org/10.1016/0097-3165(86)90059-2 CrossRefGoogle Scholar
[3] Becker, H. and Kechris, A. S., The descriptive set theory of Polish group actions. London Mathematical Society Lecture Note Series, 232, Cambridge University Press, Cambridge, 1996.Google Scholar
[4] Bessaga, C. and Pełczyński, A., The estimated extension theorem, homogeneous collections and skeletons, and their applications to the topological classification of linear matrix spaces and convex sets. Fund. Math. 69(1970), 153–190.CrossRefGoogle Scholar
[5] Brian, W., van Mill, J., and Suabedissen, R., Homogeneity and generalizations of 2-point sets. Houston J. Math, to appear. http://www.few.vu.nl/_vanmill/papers/preprints/SliceSets.pdf Google Scholar
[6] Charatonik, J. J. and Maćkowiak, T., Around Effros' theorem. Trans. Amer. Math. Soc. 298(1986), no. 2, 579–602.Google Scholar
[7] I. M. Dektjarev, , A closed graph theorem for ultracomplete spaces. Russian, Dokl. Akad. Nauk SSSR 157(1964), 771–773.Google Scholar
[8] Effros, E. G., Transformation groups and C*-algebras. Ann. of Math. 81(1965), 38–55. http://dx.doi.org/10.2307/1970381 CrossRefGoogle Scholar
[9] Fitzpatrick, B., Jr. and Zhou, H-X., Countable dense homogeneity and the baire property. Topology Appl. 43(1992), no. 1, 1–14. http://dx.doi.org/10.1016/0166-8641(92)90148-S CrossRefGoogle Scholar
[10] Hausdorff, F., Über innere Abbildungen. Fund. Math. 23(1934),no. 1, 279–291.CrossRefGoogle Scholar
[11] Hoht, A.i, Another alternative proof of Effros’ theorem. Topology Proc. 12(1987), no. 2, 295–298.Google Scholar
[12] Homma, T., On the embedding of polyhedra in manifolds., Yokohama Math. J. 10(1962), 5–10.Google Scholar
[13] Hrušák, M. and Zamora Avilés, B., Countable dense homogeneity of definable spaces. Proc. Amer. Math. Soc. 133(2005), no. 11, 3429–3435. http://dx.doi.org/10.1090/S0002-9939-05-07858-5 CrossRefGoogle Scholar
[14] Hurewicz, W., Relativ perfekte Teile von Punktmengen und Mengen (A). Fund. Math. 12(1928), 78–109.CrossRefGoogle Scholar
[15] Kechris, A. S., Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, New York, 1995.Google Scholar
[16] Levi, S., On Baire cosmic spaces. In: General topology and its relations to modern analysis and algebra, V (Prague, 1981), Sigma Ser. Pure Math., 3, Heldermann, Berlin, 1983, pp. 450–454.Google Scholar
[17] Morley, M., The number of countable models. J. Symbolic Logic 35(1970), 14–18. http://dx.doi.org/10.2307/2271150 CrossRefGoogle Scholar
[18] Ungar, G. S., On all kinds of homogeneous spaces. Trans. Amer. Math. Soc. 212(1975), 393–400. http://dx.doi.org/10.1090/S0002-9947-1975-0385825-3 CrossRefGoogle Scholar
[19] Ungar, G. S., Countable dense homogeneity and n-homogeneity. Fund. Math. 99(1978), no. 3, 155–160.CrossRefGoogle Scholar
[20] van Mill, J., The infinite-dimensional topology of function spaces. North-Holland Mathematical Library, 64, North-Holland Publishing Co., Amsterdam, 2001.Google Scholar
[21] van Mill, J., A note on Ford's example. Topology Proc. 28(2004), no. 2, 689–694.Google Scholar
[22] van Mill, J., A note on the Effros theorem. Amer. Math. Monthly. 111(2004), no. 9, 801–806. http://dx.doi.org/10.2307/4145191 CrossRefGoogle Scholar
[23] van Mill, J., On countable dense and strong n-homogeneity. Fund. Math. 214(2011), no. 3, 215–239. http://dx.doi.org/10.4064/fm214-3-2 CrossRefGoogle Scholar
[24] Vaught, R. L., Denumerable models of complete theories. In: Infinitistic Methods (Proc. Sympos. Foundations of Math.,Warsaw, 1959), Pergamon, Oxford; Państwowe Wydawnictwo Naukowe,Warsaw, 1961, pp. 303–321.Google Scholar