Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T18:00:11.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Multipliers on Vector Valued Bergman Spaces

Published online by Cambridge University Press:  20 November 2018

Oscar Blasco  and
José Luis Arregui
Oscar Blasco
Affiliation:
Departamento de Análisis Matemático, Universidad de Valencia, 46100 Burjassot, Valencia, Spain, email: oblasco@uv.es
José Luis Arregui
Affiliation:
Departamento de Matemáticas, Universidad de Zaragoza, 50005 Zaragoza, Spain, email: arregui@posta.unizar.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $X$ be a complex Banach space and let 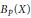${{B}_{p}}\left( X \right)$ denote the vector-valued Bergman space on the unit disc for 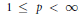$1\,\le \,p\,<\,\infty $. A sequence 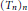${{\left( {{T}_{n}} \right)}_{n}}$ of bounded operators between two Banach spaces $X$ and 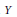$Y$ defines a multiplier between 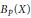${{B}_{p}}\left( X \right)$ and 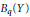${{B}_{q}}\left( Y \right)$ (resp. 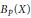${{B}_{p}}\left( X \right)$ and 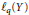${{l}_{q}}\left( Y \right)$) if for any function 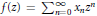$f\left( z \right)\,=\,\sum _{n=0}^{\infty }\,{{x}_{n}}{{z}^{n}}$ in 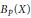${{B}_{p}}\left( X \right)$ we have that 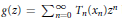$g\left( z \right)\,=\,\sum _{n=0}^{\infty }\,{{T}_{n}}\left( {{x}_{n}} \right){{z}^{n}}$ belongs to 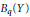${{B}_{q}}\left( Y \right)$ (resp. ${{\left( {{T}_{n}}\left( {{x}_{n}} \right) \right)}_{n}}\,\in \,{{\ell }_{q}}\left( Y \right)$). Several results on these multipliers are obtained, some of them depending upon the Fourier or Rademacher type of the spaces $X$ and 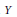$Y$. New properties defined by the vector-valued version of certain inequalities for Taylor coefficients of functions in 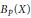${{B}_{p}}\left( X \right)$ are introduced.

Keywords

42A4546E40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 6 , 01 December 2002 , pp. 1165 - 1186
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Amann, H., Operator-valued Fourier multipliers, vector valued Besov spaces and applications. Math. Nachr. 186 (1997), 15–56.Google Scholar
[2] Anderson, J. M., Coefficient multipliers and Sobolev spaces. J. Analysis 1 (1993), 13–19.Google Scholar
[3] Anderson, J. M., Clunie, J. and Pommerenke, C., On Bloch functions and normal functions. J. Reine Angew.Math. 270 (1974), 12–37.Google Scholar
[4] Berg, J. and Löfstrom, J., Interpolation spaces. An introduction. Springer-Verlag, Berlin-New York, 1973.Google Scholar
[5] Arregui, J. L. and Blasco, O., Bergman and Bloch spaces of vector valued functions. To appear.Google Scholar
[6] Blasco, O., Spaces of vector valued analytic functions and applications. London Math. Soc. Lecture Note Ser. 158 (1990), 33–48.Google Scholar
[7] Blasco, O., Operators on weighted Bergman spaces and applications. Duke Math. J. 66 (1992), 443–467.Google Scholar
[8] Blasco, O., Multipliers on weighted Besov spaces of analytic functions. Contemp.Math. 144 (1993), 23–33.Google Scholar
[9] Blasco, O., A characterization of Hilbert spaces in terms of multipliers between spaces of vector valued analytic functions. Michigan Math. J. 42 (1995), 537–543.Google Scholar
[10] Blasco, O., Vector valued analytic functions of bounded mean oscillation and geometry of Banach spaces. Illinois J. Math. 41 (1997), 532–558.Google Scholar
[11] Blasco, O., Multipliers on spaces of analytic functions. Canad. J. Math. 47 (1995), 44–64.Google Scholar
[12] Blasco, O., Convolution by means of bilinear maps. Contemp.Math. 232 (1999), 85–103.Google Scholar
[13] Blasco, O., Remarks on vector-valued BMOA and vector-valued multipliers. Positivity 4 (2000), 339–356.Google Scholar
[14] Blasco, O., Vector-valued Hardy inequality and B-convexity. Ark. Mat. 38 (2000), 21–36.Google Scholar
[15] Blasco, O. and Xu, Q., Interpolation between vector-valued Hardy spaces. J. Funct. Anal. 102 (1991), 331–359.Google Scholar
[16] Duren, P., Hp-spaces. Academic Press, New York, 1970.Google Scholar
[17] Duren, P. L., Romberg, B. W. and Shields, A. L., Linear functionals on Hp spaces, 0 < p < 1. J. Reine Angew.Math. 238 (1969), 32–60.Google Scholar
[18] Duren, P. L. and Shields, A. L., Coefficient multipliers of Hp and Bp spaces. Pacific J. Math. 32 (1970), 69–78.Google Scholar
[19] Flett, T. M., On the rate of growth of mean values of holomorphic and harmonic functions. Proc. LondonMath. Soc. 20 (1976), 749–768.Google Scholar
[20] Garćà-Cuerva, J., Kazarian, K. S., Kolyada, V. I. and Torrea, J. L., Vector-valued Hausdorff-Young inequality and applications. Russian Math. Surveys 53 (1998), 435–13.Google Scholar
[21] Garnett, J. B., Bounded analytic functions. Academic Press, New York, 1981.Google Scholar
[22] Gaudry, G. I., Jefferies, B. R. F. and Ricker, W. F., Vector-valued multipliers. Convolution with operator-valued measures. Dissertationes Math. 385, 2000.Google Scholar
[23] Hardy, G. H. and Littlewood, J. E., Some properties of fractional integrals, II. Math. Z. 34 (1932), 403–439.Google Scholar
[24] Jevtic, M. and Jovanovic, I., Coefficient multipliers of mixed norm spaces. Canad. Math. Bull. 36 (1993), 283–285.Google Scholar
[25] Jevtic, M. and Pavlovic, M., Coefficient multipliers on spaces of analytic functions. Acta Sci. Math. (Szeged) 64 (1998), 531–545.Google Scholar
[26] Kellogg, C. N., An extension of Hausdorff-Young theorem. Michigan Math. J. 18 (1971), 121–127.Google Scholar
[27] Mateljevic, M. and Pavlovic, M., Lp-behaviour of the integral means of analytic functions. Studia Math. 77 (1984), 219–237.Google Scholar
[28] Maurey, B. and Pisier, G., Séries de variables aléatoires vectorielles indépendantes et propriétés géométriques des espaces de Banach. Studia Math. 58 (1976), 45–90.Google Scholar
[29] Peetre, J., Sur la transformation de Fourier des fonctions à valeurs vectorielles. Rend. Sem. Mat. Univ. Padova 42 (1969), 15–46.Google Scholar
[30] Shields, A. L. and Williams, D. L., Bounded projections, duality and multipliers in spaces of analytic functions. Trans. Amer. Math. Soc. 162 (1971), 287–302.Google Scholar
[31] Vukotic, D., On the coefficient multipliers of Bergman spaces. J. London Math. Soc. 50 (1994), 341–348.Google Scholar
[32] Weis, L., Operator valued Fourier multiplier theorems and maximal regularity. Math. Ann. 319 (2001), 735–758.Google Scholar
[33] Wojtaszczyk, P., On multipliers into Bergman spaces and Nevalinna class. Canad. Math. Bull. 33 (1990), 151–161.Google Scholar
[34] Zhu, K., Operators on Bergman spaces. Marcel Dekker, Inc., New York, 1990.Google Scholar
[35] Zygmund, A., Trigonometric series. Cambrigde University Press, New York, 1959.Google Scholar