Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T18:37:16.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Solvability of Laplacian Difference Operators Arising from the Discrete Heisenberg Group

Published online by Cambridge University Press:  20 November 2018

Keri A. Kornelson
Keri A. Kornelson*
Affiliation:
Department of Mathematics and Computer Science, Grinnell College, Grinnell, Iowa USA, 50112-1690, e-mail: kornelso@math.grinnell.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Differential operators 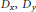${{D}_{x,}}\,{{D}_{y}}$, and 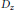${{D}_{z}}$ are formed using the action of the 3-dimensional discrete Heisenberg group $G$ on a set $S$, and the operators will act on functions on $S$. The Laplacian operator $L\,=\,D_{x}^{2}+D_{y}^{2}+D_{z}^{2}$ is a difference operator with variable differences which can be associated to a unitary representation of $G$ on the Hilbert space 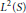${{L}^{2}}\left( S \right)$. Using techniques from harmonic analysis and representation theory, we show that the Laplacian operator is locally solvable.

Keywords

43A8522D1039A70discrete Heisenberg groupunitary representationlocal solvabilitydifference operator
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 3 , 01 June 2005 , pp. 598 - 615
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Lawrence W., Baggett, Processing a radar signal and representations of the discrete Heisenberg group. Colloq. Math. LX/LXI 1(1990), 195–203.Google Scholar
[2] Lawrence W., Baggett, Functional Analysis: A Primer. Marcel Dekker, Inc., 1992.Google Scholar
[3] Lawrence, Corwin and Linda Preiss Rothschild, Necessary conditions for local solvability of homogeneous left invariant differential operators on nilpotent Lie groups. Acta Math. 147(1981), 265–288.Google Scholar
[4] Gerald B., Folland, Harmonic Analysis in Phase Space. Ann. of Math. Stud., Princeton University Press.Google Scholar
[5] Gerald B., Folland, A Course in Abstract Harmonic Analysis. CRC Press, Inc., 1995.Google Scholar
[6] Roger E., Howe, On the role of the Heisenberg group in harmonic analysis. Bull. Amer. Math. Soc. 3(1980), 821–843.Google Scholar
[7] George W., Mackey, Induced representations of locally compact groups, I. Ann. of Math. 55(1952), 101–139.Google Scholar
[8] Detlef, Müller and Fulvio, Ricci, Analysis of second order differential operators on the Heisenberg group I. Invent.Math. 101(1990), 545–582.Google Scholar
[9] James R., Munkres, Topology: A First Course. Prentice-Hall, Inc., 1975.Google Scholar
[10] Arlan, Ramsay, Nontransitive quasi-orbits in Mackey's analysis of group extensions. Acta Math. 137(1976), 17–48.Google Scholar
[11] Melissa Anne, Richey, Locally Solvable Operators on the Discrete Heisenberg Group. PhD thesis, University of Colorado at Boulder, 1999.Google Scholar
[12] Linda Preiss, othschild, Local solvability of left invariant differential operators on the Heisenberg group. Proc. Amer.Math. Soc. 74(1979), 383–388.Google Scholar
[13] Eckart, Schulz and Keith F., Taylor, Extensions of the Heisenberg group and wavelet analysis in the plane. CRMProc. Lecture Notes 18(1999), 217–225.Google Scholar