Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-06T05:54:39.607Z Has data issue: false hasContentIssue false
  • English
  • Français

The Level 2 and 3 Modular Invariants for the Orthogonal Algebras

Published online by Cambridge University Press:  20 November 2018

Terry Gannon
Terry Gannon*
Affiliation:
Department of Mathematical Sciences, University of Alberta, Edmonton, Alberta, T6G 2G1 email: tgannon@math.ualberta.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The ‘1-loop partition function’ of a rational conformal field theory is a sesquilinear combination of characters, invariant under a natural action of 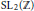$\text{S}{{\text{L}}_{2}}(\mathbb{Z})$, and obeying an integrality condition. Classifying these is a clearly defined mathematical problem, and at least for the affine Kac-Moody algebras tends to have interesting solutions. This paper finds for each affine algebra 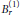$B_{r}^{\left( 1 \right)}$ and $D_{r}^{(1)}$ all of these at level 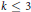$k\le 3$. Previously, only those at level 1 were classified. An extraordinary number of exceptionals appear at level 2—the 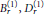$B_{r}^{(1)},D_{r}^{(1)}$ level 2 classification is easily the most anomalous one known and this uniqueness is the primary motivation for this paper. The only level 3 exceptionals occur for 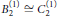$B_{2}^{(1)}\cong C_{2}^{(1)}$ and 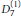$D_{7}^{(1)}$. The 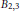${{B}_{2,3}}$ and 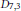${{D}_{7,3}}$ exceptionals are cousins of the 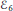${{\varepsilon }_{6}}$-exceptional and 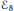${{\varepsilon }_{8}}$-exceptional, respectively, in the 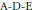$\text{A-D-E}$ classification for 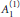$A_{1}^{(1)}$, while the level 2 exceptionals are related to the lattice invariants of affine 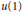$u(1)$.

Keywords

17B6781T40Kac-Moody algebraconformal field theorymodular invariants
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 3 , 01 June 2000 , pp. 503 - 521
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Bauer, M., Coste, A., Itzykson, C. and Ruelle, Ph., Comments on the links between SU(3) modular invariants, simple factors in the Jacobian of Fermat curves, and rational triangular billiards. J. Geom. Phys. 22(1997), 134–189.Google Scholar
[1a] Ruelle, Ph., Thiran, E. and Weyers, J., Implications of an arithmetic symmetry of the commutant for modular invariants . Nucl. Phys. B402(1993), 693–708.Google Scholar
[2] Bernard, D., String characters from Kac-Moody automorphisms . Nucl. Phys. B288(1987), 628–648.Google Scholar
[3] Cappelli, A., Itzykson, C. and Zuber, J.-B., The A-D-E classification of A (1) 1 and minimal conformal field theories. Commun. Math. Phys. 113(1987), 1–26.Google Scholar
[4] Coste, A. and Gannon, T., Remarks on Galois symmetry in rational conformal field theories . Phys. Lett. B323(1994), 316–321.Google Scholar
[5] Evans, D. E. and Kashahigashi, Y., Quantum Symmetries on Operator Algebras. Oxford University Press, Oxford, 1998.Google Scholar
[6] Fuchs, J., Schellekens, A. N. and Schweigert, C., Galois modular invariants of WZW models . Nucl. Phys. B437(1995), 667–694.Google Scholar
[7] Gannon, T., WZW commutants, lattices, and level-one partition functions . Nucl. Phys. B396(1993), 708–736.Google Scholar
[8] Gannon, T., Symmetries of the Kac-Peterson modular matrices of affine algebras. Invent. Math. 122(1995), 341–357.Google Scholar
[9] Gannon, T., The classification of SU(3) modular invariants revisited. Ann. Inst. H. Poincaré Phys. Théor. 65(1996), 15–56.Google Scholar
[10] Gannon, T., The level 2 and 3 modular invariant partition functions for SU(n). Lett.Math. Phys. 39(1997), 289–298.Google Scholar
[11] Gannon, T., U(1)m modular invariants, N = 2 minimal models, and the quantum Hall effect. Nucl. Phys. 491(1997), 659–688.Google Scholar
[12] Gannon, T., The Cappelli-Itzykson-Zuber A-D-E classification. Preprint math.QA/9902064; Rev.Math. Phys., to appear.Google Scholar
[13] Gannon, T., Kac-Peterson, Perron-Frobenius, and the classification of conformal field theories. Preprint qalg/ 9510026; T. Gannon, The ADE7-type invariants of affine algebras. In preparation.Google Scholar
[14] Gannon, T., Ruelle, Ph. and Walton, M. A., Automorphism modular invariants of current algebras. Commun. Math. Phys. 179(1996), 121–156.Google Scholar
[15] Hanany, A. and He, Y.-H., Non-abelian finite gauge theories. Preprint hep-th/9811183.Google Scholar
[16] Kac, V. G. and Peterson, D., Infinite-dimensional Lie algebras, theta functions and modular forms. Adv. Math. 53(1984), 125–264.Google Scholar
[17] Kac, V. G. and Wakimoto, M., Modular and conformal constraints in representation theory of affine algebras. Adv. Math. 70(1988), 156–236.Google Scholar
[18] Koblitz, N. and Rohrlich, D., Simple factors in the Jacobian of a Fermat curve. Canad. J. Math. 30(1978), 1183–1205.Google Scholar
[19] Mlawer, E. J., Naculich, S. G., Riggs, H. A. and Schnitzer, H. J., Group-level duality of WZW fusion coefficients and Chern-Simons link observables. Nucl. Phys. B352(1991), 863–896.Google Scholar
[20] Schellekens, A. N., Cloning SO(N)level 2 . Internat. J. Modern Phys. A14(1999), 1283–1291.Google Scholar
[21] Schellekens, A. N. and Yankielowicz, S., Modular invariants from simple currents. An explicit proof. Phys. Lett. B227(1989), 387–391.Google Scholar
[22] Slodowy, P., Platonic solids, Kleinian singularities, and Lie groups . Lecture Notes in Math. 1008, Springer-Verlag, New York, 1983, 102–138.Google Scholar
[23] Verstegen, D., New exceptional modular invariant partition functions for simple Kac-Moody algebras. Nucl. Phys. B346(1990), 349–386.Google Scholar