Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T18:50:41.446Z Has data issue: false hasContentIssue false
  • English
  • Français

The Homology of Singular Polygon Spaces

Published online by Cambridge University Press:  20 November 2018

Yasuhiko Kamiyama
Yasuhiko Kamiyama*
Affiliation:
Department of Mathematics University of the Ryukyus Nishihara-Cho Okinawa 903-01 Japan, e-mail: kamiyama@sci.u-ryukyu.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ${{M}_{n}}$ be the variety of spatial polygons 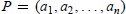$P\,=\,({{a}_{1}},\,{{a}_{2}},...,{{a}_{n}})$ whose sides are vectors 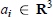${{a}_{i}}\,\in \,{{\mathbf{R}}^{3}}$ of length 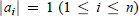$\left| {{a}_{i}} \right|\,=\,1\,(1\,\le \,i\,\le \,n)$, up to motion in 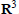${{\mathbf{R}}^{3}}$. It is known that for odd $n$, ${{M}_{n}}$ is a smooth manifold, while for even $n$, ${{M}_{n}}$ has cone-like singular points. For odd $n$, the rational homology of ${{M}_{n}}$ was determined by Kirwan and Klyachko [6], [9]. The purpose of this paper is to determine the rational homology of ${{M}_{n}}$ for even $n$. For even $n$, let 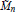${{\tilde{M}}_{n}}$ be the manifold obtained from ${{M}_{n}}$ by the resolution of the singularities. Then we also determine the integral homology of 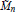${{\tilde{M}}_{n}}$.

Keywords

14D2057N65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 3 , 01 June 1998 , pp. 581 - 594
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Andreotti, A. and Frankel, T., The Lefschetz theorem on hyperplane sections. Ann. of Math. 69(1959), 713– 717.Google Scholar
2. Kamiyama, Y., Topology of equilateral polygon linkages. Topology Appl. 68(1996), 13–31.Google Scholar
3. Kamiyama, Y. and Tezuka, M., Topology and geometry of equilateral polygon linkages in the Euclidean plane. Preprint.Google Scholar
4. Kamiyama, Y., Remarks on the topology of spatial polygon spaces. Preprint.Google Scholar
5. Kapovich, M. and Millson, J., The symplectic geometry of polygons in the Euclidean space. J. Differential Geom. 44(1996), 479–513.Google Scholar
6. Kirwan, F., The cohomology of quotients in symplectic and algebraic geometry. Math. Notes 31, Princeton University Press, Princeton, NJ, 1984.Google Scholar
7. Kirwan, F., The cohomology rings of moduli spaces of bundles over Riemann surfaces. J. Amer.Math. Soc. 5(1992), 853–906.Google Scholar
8. Klyachko, A., Equivariant vector bundles on toric varieties. Math. USSR Izv. 53(1989), 1001–1039.(Russian).Google Scholar
9. Klyachko, A., Spatial polygons and stable configurations of points in the projective line. Algebraic geometry and its applications, Aspects of Math. 25(1994), 67–84.Google Scholar