Published online by Cambridge University Press: 20 November 2018
Let 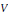 $V$ be an analytic variety in some open set in
$V$ be an analytic variety in some open set in  ${{\mathbb{C}}^{n}}$ which contains the origin and which is purely
${{\mathbb{C}}^{n}}$ which contains the origin and which is purely 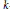 $k$-dimensional. For a curve
$k$-dimensional. For a curve  $\gamma $ in
$\gamma $ in  ${{\mathbb{C}}^{n}}$, defined by a convergent Puiseux series and satisfying
${{\mathbb{C}}^{n}}$, defined by a convergent Puiseux series and satisfying 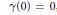 $\gamma (0)\,=\,0$, and
$\gamma (0)\,=\,0$, and 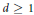 $d\,\ge \,1$, define
$d\,\ge \,1$, define 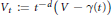 ${{V}_{t}}\,:=\,{{t}^{-d}}\,\left( V\,-\,\gamma \left( t \right) \right)$. Then the currents defined by
${{V}_{t}}\,:=\,{{t}^{-d}}\,\left( V\,-\,\gamma \left( t \right) \right)$. Then the currents defined by  ${{V}_{t}}$ converge to a limit current
${{V}_{t}}$ converge to a limit current 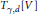 ${{T}_{\gamma ,d}}\left[ V \right]$ as
${{T}_{\gamma ,d}}\left[ V \right]$ as  $t$ tends to zero.
$t$ tends to zero. 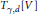 ${{T}_{\gamma ,d}}\left[ V \right]$ is either zero or its support is an algebraic variety of pure dimension
${{T}_{\gamma ,d}}\left[ V \right]$ is either zero or its support is an algebraic variety of pure dimension 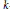 $k$ in
$k$ in  ${{\mathbb{C}}^{n}}$. Properties of such limit currents and examples are presented. These results will be applied in a forthcoming paper to derive necessary conditions for varieties satisfying the local Phragmén-Lindelöf condition that was used by Hörmander to characterize the constant coefficient partial differential operators which act surjectively on the space of all real analytic functions on
${{\mathbb{C}}^{n}}$. Properties of such limit currents and examples are presented. These results will be applied in a forthcoming paper to derive necessary conditions for varieties satisfying the local Phragmén-Lindelöf condition that was used by Hörmander to characterize the constant coefficient partial differential operators which act surjectively on the space of all real analytic functions on 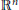 ${{\mathbb{R}}^{n}}$.
${{\mathbb{R}}^{n}}$.