No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In this paper, we find configurations of points in  $n$-dimensional projective space
$n$-dimensional projective space 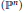 $\left( {{\mathbb{P}}^{n}} \right)$ which simultaneously generalize both
$\left( {{\mathbb{P}}^{n}} \right)$ which simultaneously generalize both  $k$-configurations and reduced 0-dimensional complete intersections. Recall that
$k$-configurations and reduced 0-dimensional complete intersections. Recall that  $k$-configurations in
$k$-configurations in  ${{\mathbb{P}}^{2}}$ are disjoint unions of distinct points on lines and in
${{\mathbb{P}}^{2}}$ are disjoint unions of distinct points on lines and in 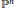 ${{\mathbb{P}}^{n}}$ are inductively disjoint unions of
${{\mathbb{P}}^{n}}$ are inductively disjoint unions of  $k$-configurations on hyperplanes, subject to certain conditions. Furthermore, the Hilbert function of a
$k$-configurations on hyperplanes, subject to certain conditions. Furthermore, the Hilbert function of a  $k$-configuration is determined from those of the smaller
$k$-configuration is determined from those of the smaller  $k$-configurations. We call our generalized constructions
$k$-configurations. We call our generalized constructions  ${{k}_{D}}$-configurations, where
${{k}_{D}}$-configurations, where 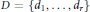 $D\,=\,\left\{ {{d}_{1}},\ldots ,{{d}_{r}} \right\}$ (a set of
$D\,=\,\left\{ {{d}_{1}},\ldots ,{{d}_{r}} \right\}$ (a set of  $r$ positive integers with repetition allowed) is the type of a given complete intersection in
$r$ positive integers with repetition allowed) is the type of a given complete intersection in 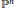 ${{\mathbb{P}}^{n}}$. We show that the Hilbert function of any
${{\mathbb{P}}^{n}}$. We show that the Hilbert function of any  ${{k}_{D}}$-configuration can be obtained from those of smaller
${{k}_{D}}$-configuration can be obtained from those of smaller  ${{k}_{D}}$-configurations. We then provide applications of this result in two different directions, both of which are motivated by corresponding results about
${{k}_{D}}$-configurations. We then provide applications of this result in two different directions, both of which are motivated by corresponding results about  $k$-configurations.
$k$-configurations.