Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-21T19:56:33.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalization of Schwarz-Pick Lemma to Invariant Volume

Published online by Cambridge University Press:  20 November 2018

K. T. Hahn  and
Josephine Mitchell
K. T. Hahn
Affiliation:
The Pennsylvania State University, University Park, Pennsylvania
Josephine Mitchell
Affiliation:
Mathematics Research Center, University of Wisconsin, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give an extension of (6, Theorem 1), using a similar method of proof, to every homogeneous Siegel domain of second kind which can be mapped biholomorphically into a Kâhler manifold of a certain class 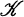(Theorem 1). Then by a well-known result of Vinberg, Gindikin, and Pjateckiï-Sapiro (10) that every bounded homogeneous domain D,contained in a complex euclidean space CN,can be mapped biholomorphically onto an affinely homogeneous Siegel domain of second kind, the theorem follows for D(Theorem 2). (6, Theorem 1) is a generalization of the Ahlfors version of the Schwarz-Pick lemma in C1(1) to invariant volume for a star-like homogeneous bounded domain in CN;see also (4). In § 3 we give the inequality for a special non-symmetric Siegel domain of second kind using an explicit form of TD(z, )due to Lu (7).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 669 - 674
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Ahlfors, L. V., An extension of Schwarz's lemma, Trans. Amer. Math. Soc. 43 (1938), 359–364.Google Scholar
2. Behnke, H. and Thullen, P., Théorie der Funktionen mehrer komplexer Verdnderlichen, Ergebnisse der Math, und ihrer Grenzgebiete, Band 3 (Springer, Berlin, 1934).Google Scholar
3. Bergman, S., Sur les fonctions orthogonales de plusieurs variables complexes avec les applications à la théorie des fonctions analytiques, Mém. Sci. Math. no. 106 (Gauthier-Villars, Paris, 1947).Google Scholar
4. Bergman, S., Zur Théorie von pseudokonformen Abbildungen, Recueil Math. (N.S.) Nouv. sér. 1 (43) (1936), 79–96.Google Scholar
5. Fuks, B. A., Special chapters in the theory of analytic functions of several complex variables. Transi. Math. Monog., Vol. 14 (Amer. Math. Soc, Providence, R. I., 1965; Gosudarstv. Izdat. Fiz.-Mat. Lit., Moscow, 1963).Google Scholar
6. Hahn, K. T. and Mitchell, Josephine, Generalization of Schwarz-Pick lemma to invariant volume in a Kàhler manifold, Trans. Amer. Math. Soc. 128 (1967), 221–231.Google Scholar
7. Lu, R. Q., Harmonic functions in a class of non-symmetric transitive domains, Acta. Math. Sinica 15 (1965), No. 5, 614–650.Google Scholar
8. Pjateckiï-Sapiro, I. I., Geometry of classical domains and theory of automorphic functions (Fizmatgiz, Moscow, 1961).Google Scholar
9. Schaefer, H. H., Topological vector spaces (Macmillan, New York, 1966).Google Scholar
10. Vinberg, E. B., Gindikin, S. G., and Pjateckiï-Sapiro, I. I., Classification and canonical realization of complex homogeneous domains, Trudy Moscow Mat. Obsc. 12 (1963), 359-388 = Transi. Moscow Math. Soc. 12 (1963), 404–437.Google Scholar