Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T03:38:01.368Z Has data issue: false hasContentIssue false
  • English
  • Français

Fourier Spaces and Completely Isometric Representations of Arens Product Algebras

Part of: Abstract harmonic analysis Linear spaces and algebras of operators Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  07 January 2019

Ross Stokke
Ross Stokke*
Affiliation:
Department of Mathematics and Statistics, University of Winnipeg, Winnipeg, MB R3B 2E9, Canada Email: r.stokke@uwinnipeg.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by the definition of a semigroup compactication of a locally compact group and a large collection of examples, we introduce the notion of an (operator) homogeneous left dual Banach algebra (HLDBA) over a (completely contractive) Banach algebra 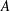$A$. We prove a Gelfand-type representation theorem showing that every HLDBA over A has a concrete realization as an (operator) homogeneous left Arens product algebra: the dual of a subspace of 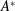$A^{\ast }$ with a compatible (matrix) norm and a type of left Arens product $\Box$. Examples include all left Arens product algebras over 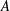$A$, but also, when 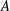$A$ is the group algebra of a locally compact group, the dual of its Fourier algebra. Beginning with any (completely) contractive (operator) 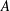$A$-module action 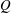$Q$ on a space 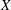$X$, we introduce the (operator) Fourier space 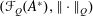$({\mathcal{F}}_{Q}(A^{\ast }),\Vert \cdot \Vert _{Q})$ and prove that 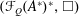$({\mathcal{F}}_{Q}(A^{\ast })^{\ast },\Box )$ is the unique (operator) HLDBA over $A$ for which there is a weak$^{\ast }$-continuous completely isometric representation as completely bounded operators on $X^{\ast }$ extending the dual module representation. Applying our theory to several examples of (completely contractive) Banach algebras $A$ and module operations, we provide new characterizations of familiar HLDBAs over A and we recover, and often extend, some (completely) isometric representation theorems concerning these HLDBAs.

Keywords

Banach algebraoperator spaceArens productgroup algebraFourier algebra

MSC classification

Primary: 47L10: Algebras of operators on Banach spaces and other topological linear spaces
Secondary: 43A20: $L^1$-algebras on groups, semigroups, etc. 43A30: Fourier and Fourier-Stieltjes transforms on nonabelian groups and on semigroups, etc. 46H15: Representations of topological algebras 46H25: Normed modules and Banach modules, topological modules (if not placed in or ) 47L25: Operator spaces (= matricially normed spaces)
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 3 , June 2019 , pp. 717 - 747
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This research was partially supported by an NSERC grant.

References

Arens, R., The adjoint of a bilinear operation . Proc. Amer. Math. Soc. 2(1951), 839–848. https://doi.org/10.2307/2031695.Google Scholar
Arsac, G., Sur l’espace de Banach engendré par les coefficients d’une représentation unitaire . Publ. Dép. Math. (Lyon) 13(1976), 1–101.Google Scholar
Bekka, M. E. B., Amenable unitary representations of locally compact groups . Invent. Math. 100(1990), 383–401. https://doi.org/10.1007/BF01231192.Google Scholar
Berglund, J. F., Junghenn, H., and Milnes, P., Analysis on semigroups: Function spaces, compactifications, representations. Canadian Mathematical Society Series of Monographs and Advanced Texts, John Wiley, New York, 1989.Google Scholar
Conway, J., A course in functional analysis. Second edition. Graduate Texts in Mathematics, 96. Springer-Verlag, New York, 1990.Google Scholar
P. C. Curtis, Jr. and A. Figá-Talamanca, Factorization theorems for Banach algebras. In: Function algebras. Scott-Foresman, Chicago, IL, 1966, pp. 169–185.Google Scholar
Dales, H. G., Banach algebras and automatic continuity. London Mathematical Society Monographs, 24. Clarendon Press, New York, 2000.Google Scholar
Dales, H. G. and Lau, A. T.-M., The second duals of Beurling algebras. Mem. Amer. Math. Soc. 177 (2005). no. 836, vi $+$ 191 pp. https://doi.org/10.1090/memo/0836.Google Scholar
Daws, M., Dual Banach algebras: representations and injectivity. Studia Math. 178 (2007), no. 3, 231–275. https://doi.org/10.4064/sm178-3-3.Google Scholar
Effros, E. G. and Ruan, Z.-J., Operator spaces. London Mathematical Society Monographs, 23. Oxford University Press, New York, 2000.Google Scholar
Filali, M., Neufang, M., and Sangani Monfared, M., Representations of Banach algebras subordinate to topologically introverted spaces. Trans. Amer. Math. Soc. 367 (2015), no. 11, 8033–8050. https://doi.org/10.1090/tran/6435.Google Scholar
Ghahramani, F., Isometric representation of $M(G)$ on $B(H)$ . Glasgow Math. J. 23 (1982), no. 2, 119–122. https://doi.org/10.1017/S0017089500004882.Google Scholar
Hu, Z., Neufang, M., and Ruan, Z.-J., Multipliers on a new class of Banach algebras, locally compact quantum groups, and topological centres. Proc. Lond. Math. Soc. (3) 100 (2010) no. 2, 429–458. https://doi.org/10.1112/plms/pdp026.Google Scholar
Hewitt, E. and Ross, K. A., Abstract harmonic analysis II. Structure and analysis for compact groups. Analysis on locally compact Abelian groups. Grundelehern der Mathematischen Wissenschasften, 152. Springer-Verlag, New York, 1970.Google Scholar
Lau, A. T.-M., Uniformly continuous functionals on the Fourier algebra of any locally compact group . Trans. Amer. Math. Soc. 251(1979), 39–59. https://doi.org/10.2307/1998682.Google Scholar
Lau, A. T.-M., Uniformly continuous functionals on Banach algebras . Colloq. Math. 51(1987), 195–205. https://doi.org/10.4064/cm-51-1-195-205.Google Scholar
Neufang, M., Abstrakte harmonische Analyse und Modulhomomorphismen über von Neumann-Algebren. Ph.D. Thesis, Universität des Saarlandes, 2000.Google Scholar
Neufang, M., Isometric representation of convolution algebras as completely bounded module homomorphisms and a characterization of the measure algebra. Carleton University, Canada, 2001.Google Scholar
Neufang, M., Ruan, Z.-J., and Spronk, N., Completely isometric representations of $M_{c.b.}A(G)$ and $UCB(\widehat{G})$ . Trans. Amer. Math. Soc. 360 (2008), no. 3, 1133–1161. https://doi.org/10.1090/S0002-9947-07-03940-2.Google Scholar
Pisier, G., Introduction to operator space theory. London Mathematical Society Lecture Note Series, 294. Cambridge University Press, Cambridge, 2003. https://doi.org/10.1017/CBO9781107360235.Google Scholar
Spronk, N. and Stokke, R., Matrix coefficients of unitary representations and associated compactifications of locally compact groups. Indiana Univ. Math. J. 62 (2013), no. 1, 99–148. https://doi.org/10.1512/iumj.2013.62.4825.Google Scholar
Stokke, R., Homomorphisms of convolution algebras. J. Funct. Anal. 261 (2011), no. 12, 3665–3695. https://doi.org/10.1016/j.jfa.2011.08.014.Google Scholar
Stokke, R., Amenability and modules for Arens product algebras. Q. J. Math. 66 (2015), no. 1, 295–321. https://doi.org/10.1093/qmath/hau018.Google Scholar
Størmer, E., Regular abelian Banach algebras of linear maps of operator algebras. J. Funct. Anal. 37 (1980), no. 3, 331–373. https://doi.org/10.1016/0022-1236(80)90048-8.Google Scholar
Uygul, F., A representation theorem for completely contractive dual Banach algebras. J. Operator Theory 62 (2009), no. 2, 327–340.Google Scholar