Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T11:22:32.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Endomorphism Algebras of Kronecker Modules Regulated by Quadratic Function Fields

Published online by Cambridge University Press:  20 November 2018

F. Okoh  and
F. Zorzitto
F. Okoh
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI 48202, U.S.A. e-mail: okoh@math.wayne.edu
F. Zorzitto
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: fazorzit@uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Purely simple Kronecker modules 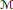$M$, built from an algebraically closed field 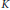$K$, arise from a triplet 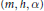$\left( m,\,h,\,\alpha \right)$ where 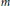$m$ is a positive integer, $h:\,K\,\cup \,\{\infty \}\,\to \,\{\infty ,\,0,\,1,\,2,\,3,\,.\,.\,.\,\}$ is a height function, and $\alpha$ is a 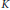$K$-linear functional on the space 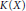$K\left( X \right)$ of rational functions in one variable 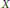$X$. Every pair 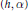$\left( h,\,\alpha \right)$ comes with a polynomial 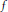$f$ in $K\left( X \right)\left[ Y\, \right]$ called the regulator. When the module 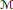$M$ admits non-trivial endomorphisms, 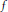$f$ must be linear or quadratic in $Y$. In that case 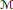$M$ is purely simple if and only if 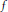$f$ is an irreducible quadratic. Then the 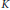$K$-algebra End 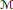$M$ embeds in the quadratic function field 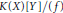${K\left( X \right)\left[ Y\, \right]}/{(f\,)}\;$. 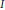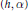For some height functions $h$ of infinite support $I$, the search for a functional $\alpha$ for which $\left( h,\,\alpha \right)$ has regulator $0$ comes down to having functions 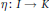$\eta \,:\,I\,\to \,K$ such that no planar curve intersects the graph of $\eta$ on a cofinite subset. 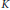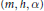If $K$ has characterictic not $2$, and the triplet $\left( m,\,h,\,\alpha \right)$ gives a purely-simple Kronecker module 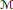$M$ having non-trivial endomorphisms, then $h$ attains the value $\infty$ at least once on 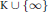$\text{K}\,\cup \,\text{ }\!\!\{\!\!\text{ }\infty \text{ }\!\!\}\!\!\text{ }$ and $h$ is finite-valued at least twice on 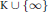$\text{K}\,\cup \,\text{ }\!\!\{\!\!\text{ }\infty \text{ }\!\!\}\!\!\text{ }$. Conversely all these $h$ form part of such triplets. The proof of this result hinges on the fact that a rational function $r$ is a perfect square in 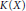$K\left( X \right)$ if and only if $r$ is a perfect square in the completions of 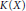$K\left( X \right)$ with respect to all of its valuations.

Keywords

16S5015A27Purely simple Kronecker moduleregulating polynomialLaurent expansionsendomorphism algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 1 , 01 February 2007 , pp. 186 - 210
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Auslander, M., Reiten, I., and Smalø, S. O., Representation Theory of Artin Algebras. Cambridge Studies in Advanced Mathematics 36, Cambridge University Press, Cambridge, 1995.Google Scholar
[2] Dean, A. and Zorzitto, F. A., A criterion for pure simplicity. J. Algebra 132(1990), no. 1, 50–71.Google Scholar
[3] Fixman, U., On algebraic equivalence between pairs of linear transformations. Trans. Amer. Math. Soc. 113(1964), 424–453.Google Scholar
[4] Fixman, U. and Okoh, F., Extensions of modules characterized by finite sequences of linear functionals. Rocky Mountain J. Math. 21(1991), no. 4, 1235–1258.Google Scholar
[5] Göbel, R. and Simson, D., Embeddings of Kronecker modules into the category of prinjective modules and the endomorphism ring problem. Colloq. Math. 75(1998), no. 2, 213–244.Google Scholar
[6] Göbel, R. and Simson, D., Rigid families and endomorphism algebras of Kronecker modules. Israel J. Math. 110(1999), 293–315.Google Scholar
[7] Lawrence, J., Okoh, F., and Zorzitto, F., Rational functions and Kronecker module. Comm. Alg. 14(1986), no. 10, 1947–1965.Google Scholar
[8] Lenzing, H., Homological transfer from finitely presented to infinite modules. In: Abelian Group Theory, Lecture Notes in Math. 1006, Springer, Berlin, 1983, pp. 734–761.Google Scholar
[9] Lenzing, H., The pure-projective dimension of torsion-free divisible modules. Comm. Alg. 12(1984), no. 5-6, 649–662.Google Scholar
[10] Lukas, F., A class of infinite rank modules over tame algebras. J. Algebra 158(1993), no. 1, 18–30.Google Scholar
[11] Neukirch, J., Algebraic Number Theory. Grundlehren der Mathematischen Wissenschaften 322, Springer-Verlag, Berlin, 1999.Google Scholar
[12] Okoh, F. and Zorzitto, F. A., A family of commutative endomorphism algebras. J. Algebra 201(1998), no. 1, 501–527.Google Scholar
[13] Okoh, F. and Zorzitto, F. A., Curves arising from Kronecker modules. Linear Algebra Appl. 365(2003), 311–348.Google Scholar
[14] Okoh, F. and Zorzitto, F. A., Commutative endomorphism algebras of torsion-free, rank-two Kronecker modules with singular height functions. Rocky Mountain J. Math. 32(2002), no. 4, 1559–1576.Google Scholar
[15] Okoh, F. and Zorzitto, F. A., Commutative algebras of rational function matrices as endomorphisms of Kronecker modules. I. Linear Algebra Appl. 374(2003), 41–62.Google Scholar
[16] Okoh, F. and Zorzitto, F. A., Commutative algebras of rational function matrices as endomorphisms of Kronecker modules. II. Linear Algebra Appl. 374(2003), 63–85 Google Scholar
[17] Ringel, C. M., Infinite-dimensional representations of finite-dimensional algebras. In: Symposia Mathematica 23, Academic Press, London, 1979, pp. 321–412.Google Scholar