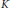Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-05T23:51:47.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalues, $K$-theory and Minimal Flows

Published online by Cambridge University Press:  20 November 2018

Benjamín A. Itzá-Ortiz
Benjamín A. Itzá-Ortiz*
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 585 King Edward Ave., Ottawa, K1N-6N5, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $(Y,\,T)$ be a minimal suspension flow built over a dynamical system 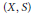$(X,\,S)$ and with (strictly positive, continuous) ceiling function 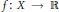$f:\,X\,\to \,\mathbb{R}$. We show that the eigenvalues of $(Y,\,T)$ are contained in the range of a trace on the ${{K}_{0}}$-group of 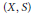$(X,\,S)$. Moreover, a trace gives an order isomorphism of a subgroup of 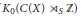${{K}_{0}}\left( C(X)\,{{\rtimes }_{S}}\,\mathbb{Z} \right)$ with the group of eigenvalues of $(Y,\,T)$. Using this result, we relate the values of $t$ for which the time-$t$ map on the minimal suspension flow is minimal with the 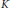$K$-theory of the base of this suspension.

Keywords

37A5537B05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 3 , 01 June 2007 , pp. 596 - 613
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Connes, A., An analogue of the Thom isomorphism for crossed products of a C*-algebra by an action of. ℝ. Adv. in Math. 39(1981), no. 1, 31–35.Google Scholar
[2] Cortez, M. I., Durand, F., Host, B., and Maass, A., Continuous and measurable eigenfunctions of linearly recurrent dynamical Cantor systems. J. London Math. Soc. 67(2003), no. 3, 790–804.Google Scholar
[3] Downarowicz, T. and Lacroix, Y., Almost 1-1 extensions of Furstenberg-Weiss type and applications to Toeplitz flows. Studia Math. 130(1998), no. 2, 149–170.Google Scholar
[4] Exel, R., Rotation numbers for automorphisms of C*-algebras. Pacific J. Math. 127(1987), no. 1, 31–89.Google Scholar
[5] Furstenberg, H., Strict ergodicity and transformation of the torus. Amer. J. Math. 83(1961), 573–601.Google Scholar
[6] Giordano, T., Putnam, I. and Skau, C., Topological orbit equivalence and C*-crossed products. J. Reine Angew.Math. 469(1995), 51–111.Google Scholar
[7] Gjerde, R. and Johansen, Ø., C*-algebras associated to non-homogeneous minimal systems and their K-theory. Math. Scand. 85(1999), no. 1, 87–104.Google Scholar
[8] Glasner, E., Ergodic Theory via Joinings. Mathematical Surveys and Monographs 101, American Mathematical Society, Providence, RI, 2003.Google Scholar
[9] Glasner, E. and Weiss, B., Weak orbit equivalence of Cantor minimal systems. Internat. J. Math 6(1995), no. 4, 559–579.Google Scholar
[10] Iwanik, A., Toeplitz flows with pure point spectrum. Studia Math. 118(1996), no. 1, 27–35.Google Scholar
[11] Katok, A. B. and Hasselblatt, B., Introduction to the modern theory of dynamical systems. Encyclopedia of Mathematics and Its Applications, Vol. 54, Cambridge University Press, Cambridge, 1995.Google Scholar
[12] Packer, J., K-theoretic invariants for C*-algebras associated to transformations and induced flows. J. Funct. Anal. 67(1986), no. 1, 25–59.Google Scholar
[13] Packer, J., Flow equivalence for dynamical systems and the corresponding C*-algebras. Oper. Theory Adv. Appl., 28, Birkhäuser, Basel, 1988, pp. 223–242.Google Scholar
[14] Phillips, N. C., Cancellation and stable rank for direct limits of recursive subhomogeneous algebras. Trans. Amer. Math. Soc. To appear.Google Scholar
[15] Pimsner, M. and Voiculescu, D., Exact sequences for K-groups and Ext-groups of certain cross-product C*-algebras. J. Operator Theory 4(1980), no. 1, 93–118.Google Scholar
[16] Putnam, I., The C*-algebras associated with minimal homeomorphisms of the Cantor set. Pacific J. Math. 136(1989), no. 2, 329–353.Google Scholar
[17] Putnam, I., Schmidt, K., and Skau, C., C*-algebras associated with Denjoy homeomorphisms of the circle. J. Operator Theory 16(1986), no. 1, 99–126.Google Scholar
[18] Riedel, N., Classification of the C*-algebras associated with minimal rotations. Pacific J. Math. 101(1982), no. 1, 153–161.Google Scholar
[19] Rieffel, M., C*-algebras associated with irrational rotations. Pacific J. Math. 93(1981), no. 2, 415–429.Google Scholar
[20] Rieffel, M., Applications of strong Morita equivalence to transformation group C*-algebras. In: Operator Algebras and Applications, Proc. Sympos. Pure Math. 38, American Mathematical Society, Providence, RI, 1982, pp. 299–310.Google Scholar
[21] Schwartzman, S., Asymptotic cycles. Ann. of Math. 66(1957), 270–284.Google Scholar
[22] de Vries, J., Elements of Topological Dynamics. Mathematics and Its Applications 257, Kluwer Academic Publishers, Dordrecht, 1993.Google Scholar
[23] Walters, P., An Introduction to Ergodic Theory. Graduate Texts in Mathematics 79, Springer-Verlag, New York, 1982.Google Scholar
[24] Wegge-Olsen, N. E., K-Theory and C*-Algebras. Oxford University Press, New York, 1993.Google Scholar