Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-10T03:03:58.661Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison Properties of the CuntzSemigroup and Applications to C* -algebras

Published online by Cambridge University Press:  20 November 2018

Joan Bosa  and
Henning Petzka
Joan Bosa
Affiliation:
School of Mathematics and Statistics, niversity of Glasgow, 15 University Gardens, G12 8QW, Glasgow, UK e-mail: joan.bosa@glasgow.ac.uk
Henning Petzka
Affiliation:
Fraunhofer Institute for Intelligent Analysis and Information Systems IAIS, Schloss Birlinghoven, 53757 Sankt Augustin, Germany and, University of Bonn, Institut für Informatik III, Rheinische Friedrich-Wilhelms-Universität Bonn, Rཫmerstraße 164, 53117 Bonn, Germany e-mail: henning.petzka@iais.fraunhofer.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study comparison properties in the category 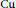$\text{Cu}$ aiming to lift results to the 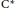${{\text{C}}^{\text{*}}}$-algebraic setting. We introduce a new comparison property and relate it to both the corona factorization property 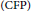$\left( \text{CFP} \right)$ and $\omega $-comparison. We show differences of all properties by providing examples that suggest that the corona factorization for 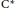${{\text{C}}^{\text{*}}}$-algebras might allow for both finite and infinite projections. In addition, we show that Rørdam's simple, nuclear 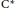${{\text{C}}^{\text{*}}}$-algebra with a finite and an inifnite projection does not have the 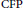$\text{CFP}$.

Keywords

46L3506F0546L0519K14classification of C*-algebrascuntz semigroup
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 1 , 01 February 2018 , pp. 26 - 52
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Ara, P. and Pardo, E., Refinement monoids with weak comparability and applications to regular rings and C* -algebras. Proc. Amer. Math. Soc. 124(1996), 715–750.http://dx.doi.org/10.1090/S0002-9939-96-03059-6 Google Scholar
[2] Ara, P., Perera, F., and Toms, A. S., K-theory for operator algebras, classification of C* -algebras. In: Aspects of operator algebras and applications. Contemp. Math. 534, American Mathematical Society, Providence, RI, 2011, pp. 1–71.Google Scholar
[3] Antoine, R., Bosa, J., and Perera, E., Completions of monoids with applications to the Cuntz semigroup. Int. J. Math, 22(2011), no. 6, 837–861.http://dx.doi.Org/10.1142/S0129167X11007057 Google Scholar
[4] Antoine, R., Bosa, J., Perera, F., and Petzka, H., Geometric structure of dimension functions of certain continuous fields. J. Func. Anal. 266(2014), no. 4, 2403–2423. http://dx.doi.Org/10.1016/j.jfa.2013.09.013 Google Scholar
[5] Antoine, R., Perera, F., and Thiel, H., Tensor products and regularity properties of Cuntz semigroups. To appear in Mem. Am. Math. Soc. arxiv:1410.0483v3 Google Scholar
[6] Blackadar, B., K-theory for operator algebras. Mathematical Sciences Research Institute Publications, 5. Cambridge University Press, Cambridge, 1998.Google Scholar
[7] Blackadar, B., Robert, L.,Toms, A., Tikuisis, A., and Winter, W., An algebraic approach of the radius of comparison. Trans. Amer. Math. Soc. 364(2012), No. 7, 3657–3674. http://dx.doi.Org/10.1090/S0002-9947-2012-05538-3 Google Scholar
[8] Blackadar, B. and Rordam, M., Extending states on preordered semigroups and the existence of quasitraces on C* -algebras. J. Algebra 152(1992),no. 11, 240–247.http://dx.doi.Org/10.1016/0021-8693(92)90098-7 Google Scholar
[9] Brown, N. P., Perera, F., and Toms, A., The Cuntz semigroup, the Elliott conjecture and dimension functions on C* -algebras. J. Reine. Angew. Math. 621(2008), 191–211.Google Scholar
[10] Cuntz, J., Dimension functions on simple C* -algebras. Math. Ann. 233(1978), no. 2,145–153.http://dx.doi.org/10.1007/BF01421922 Google Scholar
[11] Coward, K. T., Elliott, G. A., and Ivanescu, C.. The Cuntz semigroup as an invariant for C* -algebras. J. Reine. Angew. Math. 623(2008), 161–193.http://dx.doi.Org/10.1515/CRELLE.2008.075 Google Scholar
[12] Dadarlat, M., and Eilers, S., On the classification of nuclear C* -algebras. Proc. London Math. Soc.(3) 85(2002), no. 1,168–210.http://dx.doi.Org/10.1112/plms/85.1.168 Google Scholar
[13] Elliott, G. A. and Kucerovsky, D., An abstract Voiculescu-Brown-Douglas-Fillmore absorption theorem. Pacific J. Math. 198(2001), no. 2, 385–409.http://dx.doi.org/10.2140/pjm.2001.198.385 Google Scholar
[14] Elliott, G. A., Gong, G., and Li, L.. On the classification of simple inductive limit C*-algebras, II. The isomorphism theorem. Invent. Math. 168(2007), 249–320.http://dx.doi.org/10.1007/s00222-006-0033-y Google Scholar
[15] Elliott, G. A., Gong, G., Lin, H., and Niu, Z., On the classification of simple amenable C* -algebras with finite decomposition rank, II. arxiv:1 507.03437v2 Google Scholar
[16] Elliott, G. A., Robert, L., and Santiago, L., The cone of lower semicontinuous traces on a C* -algebra. Amer. J. Math. 133(2011), no. 4, 969–1005. http://dx.doi.Org/10.1353/ajm.2O11.0027 Google Scholar
[17] Goodearl, K. R., Partially ordered abelian groups with interpolation. Mathematical Surveys and Monographs, 20. American Mathematical Society, Providence, RI, 1986.Google Scholar
[18] Goodearl, K. R. and Handelman, D.. Rank functions and Kg of regular rings. J. Pure Appl. Algebra 7(1976), no. 2, 195–216.http://dx.doi.org/10.1016/0022-4049(76)90032-3 Google Scholar
[19] Kirchberg, E. and Rordam, M., Infinite non-simple C* -algebras: Absorbing the Cuntz algebras O∞. Adv. Math. 167(2002), no. 2, 198–264. http://dx.doi.org/10.1006/aima.2001.2041 Google Scholar
[20] Kirchberg, E. and Phillips, N. C., Embedding of exact C* -algebras in the Cuntz algebra O2. J. Reine Angew. Math. 525(2000), 17–53.http://dx.doi.org/10.1515/crll.2000.065 Google Scholar
[21] Kucerovsky, D. and Ng, P. W., S-regularity and the corona factorization property. Math. Scand. 99(2006), no. 2, 204–216.http://dx.doi.org/10.7146/math.scand.a-15009 Google Scholar
[22] Ng, P. W., The corona factorization property. In: Operator theory, operator algebras and applications. Contemp Math. 414. American Mathematical Society, Providence, RI, 2006, pp. 97–111.http://dx.doi.Org/10.1090/conm/414/07802 Google Scholar
[23] Ortega, E., Perera, E., and Rordam, M., The corona factorization property and refinement monoids. Trans. Amer. Math. Soc. 363(2011), no. 9, 4505–4525.http://dx.doi.Org/10.1090/S0002-9947-2011-05480-2 Google Scholar
[24] Ortega, E., The corona factorization property, stability, and the Cuntz semigroup of a C* -Algebra. Int. Math. Res. Notices 2012(2012), no. 1, 34–66.Google Scholar
[25] Petzka, H., The Blackadar-Handelman theorem for non-unital C* -algebras. J. Funct. Anal. 264(2013), no. 7, 1547–1564.http://dx.doi.Org/10.101 6/j.jfa.2O13.01.016 Google Scholar
[26] Robert, L., Nuclear dimension and n-comparison. Munster J. Math. 4(2011), 65–71.Google Scholar
[27] Robert, L., The cone offunctionals on the Cuntz semigroup. Math. Scand. 113(2013), no. 2,161–186.http://dx.doi.org/10.7146/math.scand.a-15568 Google Scholar
[28] Robert, L. and Rordam, M., Divisibility properties for C* -algebras. Proc. London Math. Soc. (3) 106(2013), no. 6, 1330–1370.http://dx.doi.Org/10.1112/plms/pdsO82 Google Scholar
[29] Rordam, M., A simple C*-algebra with a finite and an infinite projection. Acta Math. 191(2003), 109–142.http://dx.doi.org/10.1007/BF02392697 Google Scholar
[30] Rordam, M. and Winter, W., Thejiang-Su algebra revisited. J. Reine Angew. Math. 642(2010), 129–155.Google Scholar
[31] Toms, A. S.. On the classification problem for nuclear C* -algebras. Ann. of Math. 167(2008),1029–1044. http://dx.doi.Org/10.4007/annals.2008.167.1029 Google Scholar
[32] Toms, A. S. and Winter, W., The Elliott conjecture for Villadsen algebras of the first type. J. Funct. Anal. 256(2009), no. 5, 1311–1340.http://dx.doi.Org/10.1016/j.jfa.2008.12.015 Google Scholar
[33] Tikuisis, A., White, S., and Winter, W., Quasidiagonality of nuclear C* -algebras. To appear in Ann. of Math. arxiv:1509.08318 Google Scholar