Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T04:37:32.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Coinvariant Algebras of Finite Subgroups of SL(3;C)

Published online by Cambridge University Press:  20 November 2018

Yasushi Gomi ,
Iku Nakamura  and
Ken-ichi Shinoda
Yasushi Gomi
Affiliation:
Department of Mathematics, Sophia University, Tokyo 102-8554, Japan e-mail: gomi@mm.sophia.ac.jp
Iku Nakamura
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan e-mail: nakamura@math.sci.hokudai.ac.jp
Ken-ichi Shinoda
Affiliation:
Department of Mathematics, Sophia University, Tokyo 102-8554, Japan e-mail: shinoda@mm.sophia.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For most of the finite subgroups of 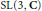$\text{SL(3,}\,\text{C)}$ we give explicit formulae for the Molien series of the coinvariant algebras, generalizing McKay's formulae 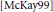$\text{ }\!\![\!\!\text{ McKay99 }\!\!]\!\!\text{ }$ for subgroups of $\text{SU(2)}$. We also study the $G $-orbit Hilbert scheme 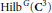$\text{Hil}{{\text{b}}^{G}}({{\mathbf{C}}^{3}})$ for any finite subgroup $G $ of 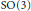$\text{SO(3)}$, which is known to be a minimal (crepant) resolution of the orbit space ${{\mathbf{C}}^{3}}/G$ . In this case the fiber over the origin of the Hilbert-Chow morphism from 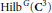$\text{Hil}{{\text{b}}^{G}}({{\mathbf{C}}^{3}})$ to ${{\mathbf{C}}^{3}}/G$ consists of finitely many smooth rational curves, whose planar dual graph is identified with a certain subgraph of the representation graph of $G $. This is an 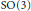$\text{SO(3)}$ version of the McKay correspondence in the $\text{SU(2)}$ case.

Keywords

14J3014J17Hilbert schemeInvariant theoryCoinvariant algebraMcKay quiverMcKay correspondence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 3 , 01 June 2004 , pp. 495 - 528
Copyright
Copyright © Canadian Mathematical Society 2004

References

[BDM16] Blichfeldt, H. F., Dickson, L. E. and Miller, G. A., Theory and Application of Finite Groups. Dover, New York, 1916.Google Scholar
[Blichfeldt05] Blichfeldt, H.F., The finite discontinuous primitive groups of collineations in three variables. Math. Ann. 63(1905), 552–572.Google Scholar
[Blichfeldt17] Blichfeldt, H.F., Finite collineation groups. Univ. Chicago Press, Chicago, 1917.Google Scholar
[BKR01] Bridgeland, T., King, A. and Reid, M., The McKay correspondence as an equivalence of derived categories. J. Amer.Math. Soc. 14(2001), 535–554.Google Scholar
[Bourbaki] Bourbaki, N., Éléments de mathétique. Chapitres 4, 5 et 6. Masson, Paris, 1981.Google Scholar
[Cohen76] Cohen, A. M., Finite complex reflection groups. Ann. Sci. École Norm. Sup. 9(1976), 379–436.Google Scholar
[GNS00] Gomi, Y., Nakamura, I. and Shinoda, K., Hilbert Schemes of G-orbits in dimension three. Kodaira's issue, Asian J. Math. (1) 4(2000), 51–70.Google Scholar
[GNS3] Gomi, Y., Nakamura, I. and Shinoda, K., Duality of the quotient ring by a regular sequence of G-invariants. In preparation.Google Scholar
[IN96] Ito, Y. and Nakamura, I., McKay correspondence and Hilbert Schemes. Proc. Japan Acad. 72(1996), 135–138.Google Scholar
[IN99] Ito, Y. and Nakamura, I., Hilbert schemes and simple singularities. New trends in algebraic geometry, Warwick, 1996, 151–233, London Math. Soc. Lecture Note Series 264, Cambridge Univ. Press, Cambridge, 1999.Google Scholar
[Lang84] Lang, S., Algebra. Second edition. Addison-Wesley Publishing Co., 1984.Google Scholar
[McKay99] McKay, J., Semi-affine Coxeter-Dynkin graphs and G ⊂ SU2(C). Canad. J. Math. 51(1999), 1226–1229.Google Scholar
[N01] Nakamura, I., Hilbert scheme of abelian group orbits. J. Algebraic Geom. 10(2001), 757–779.Google Scholar
[Springer87] Springer, T. A., Poincaré series of binary polyhedral groups and McKay's correspondence. Math. Ann. 278(1987), 99–116.Google Scholar
[Stanley79] Stanley, R. P., Invariants of finite groups and their applications to combinatorics. Bull. Amer.Math. Soc. (N.S.) 1(1979), 475–511.Google Scholar
[Steinberg64] Steinberg, R., Differential equations invariant under finite reflection groups. Trans. Amer. Math. Soc. 112(1964), 392–400.Google Scholar
[YY93] Yau, Stephen S.-T. and Yu, Y., Gorenstein quotient singularities in dimension three. Mem. Amer.Math. Soc. 105(1993).Google Scholar