Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-20T23:22:27.522Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Intrinsic Functions on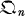

Published online by Cambridge University Press:  20 November 2018

R. E. Carlson  and
C. G. Cullen
R. E. Carlson
Affiliation:
University of Pittsburgh, Pittsburgh, Pennsylvania
C. G. Cullen
Affiliation:
University of Pittsburgh, Pittsburgh, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 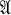be an associative algebra over the field 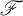and let 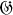be the group of all automorphisms and anti-automorphisms of 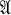which leave 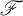elementwise invariant. A function Fwith domain 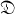and range contained in 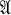is called an intrinsic functionon 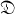if (i) 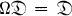for each Ω in 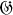and (ii) F(ΩZ) = ΩF(Z) for every Z in .

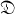Rinehart (5) has introduced and motivated the study of the class of intrinsic functions on 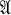, and has characterized these functions for the cases in which 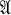is the algebra 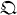of real quaternions, the algebra of n × ncomplex matrices, or the algebra 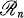of n× nreal matrices (5; 6). The algebras listed above, along with the algebra of n × nquaternion matrices, constitute the full list of possibilities for the simple direct summands of any semi-simple algebra ove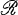r or 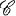; see (2).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 136 - 146
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Carlson, R. E. and Cullen, C. G., Commutativity for matrices of quaternions, Can. J. Math. 20 (1968), 21–24.Google Scholar
2. Cullen, C. G., Intrinsic functions of matrices of real quaternions, Can. J. Math. 15 (1963), 456–466.Google Scholar
3. Cullen, C. G. and Hall, C. A., Functions on semi-simple algebras. Amer. Math. Monthly 74 (1967), 14–19 Google Scholar
4. Lee, H. C., Eigenvalues and canonical forms of matrices with quaternion coefficients, Proc. Roy. Irish Acad. Sect. A 52 (1949), 253–260.Google Scholar
5. Rinehart, R. F., Elements of a theory of intrinsic functions on algebras, Duke Math. J. 27 (1960), 1–19.Google Scholar
6. Rinehart, R. F., Intrinsic functions on matrices, Duke Math. J. 28 (1961), 291–300.Google Scholar
7. Walsh, J. L., Interpolation and approximation, Amer. Math. Soc. Colloq. Publ., Vol. 20 (Amer. Math. Soc, Providence, R.I., 1935).Google Scholar
8. Wiegmann, N. A., Some theorems on matrices with real quaternion elements, Can. J. Math. 7 (1955), 191–201.Google Scholar