Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T21:07:50.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Formulae for the Lattice Point Enumerator

Published online by Cambridge University Press:  20 November 2018

U. Betke  and
K. Böröczky Jr.
U. Betke
Affiliation:
Mathematisches Institut, Universität Siegen, D–570068 Siegen, Germany email: betke@mathematik.uni-siegen.d400.de
K. Böröczky Jr.
Affiliation:
Rényi Institute of Mathematics, Budapest Pf. 127., 1364 Hungary email: carlos@math-inst.hu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 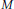$M$ be a convex body such that the boundary has positive curvature. Then by a well developed theory dating back to Landau and Hlawka for large $\lambda$ the number of lattice points in 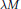$\lambda M$ is given by 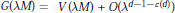$G\left( \lambda M \right)=V\left( \lambda M \right)+O\left( {{\lambda }^{d-1-\varepsilon \left( d \right)}} \right)$ for some positive 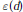$\varepsilon (d)$. Here we give for general convex bodies the weaker estimate

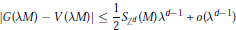$$|G\left( \lambda M \right)-V\left( \lambda M \right)|\,\le \,\frac{1}{2}{{S}_{{{Z}^{d}}}}\left( M \right){{\lambda }^{d-1}}+o\left( {{\lambda }^{d-1}} \right)$$

where ${{S}_{{{Z}^{d}}}}\left( M \right)$ denotes the lattice surface area of 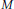$M$. The term ${{S}_{{{Z}^{d}}}}\left( M \right)$ is optimal for all convex bodies and $o\left( {{\lambda }^{d-1}} \right)$ cannot be improved in general. We prove that the same estimate even holds if we allow small deformations of 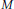$M$.

Further we deal with families 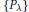$\left\{ {{P}_{\lambda }} \right\}$ of convex bodies where the only condition is that the inradius tends to infinity. Here we have

$$|G\left( {{P}_{\lambda }} \right)-V\left( {{P}_{\lambda }} \right)|\,\le \,dV\left( {{P}_{\lambda }},\,K;1 \right)+o\left( S\left( {{P}_{\lambda }} \right) \right)$$

where the convex body $K$ satisfies some simple condition, 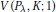$V\left( {{P}_{\lambda }},K;1 \right)$ is some mixed volume and 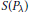$S\left( {{P}_{\lambda }} \right)$ is the surface area of 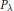${{P}_{\lambda }}$.

Keywords

11P2152C07
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 2 , 01 April 1999 , pp. 225 - 249
Copyright
Copyright © Canadian Mathematical Society 1999

References

[ABB] Arhelger, V., Betke, U. and Böröczky, K., Jr., Large finite packings Preprint, Siegen, 1996. http://www.math-inst.hu/∼carlos/abb.ps Google Scholar
[BB] Betke, U. and Böröczky, K., Jr., Finite lattice packings and the Wulff-shape. Mathematika (accepted). http://www.math-inst.hu/∼carlos/wulff.ps Google Scholar
[BH] Betke, U. and Henk, M., Estimating Sizes of a Convex Body by Successive Diameters and Widths. Mathematika 39 (1992), 247–257.Google Scholar
[BW] Betke, U. and Wills, J. M., Stetige und diskrete Funktionale konvexer Körper. In: Contributions to Geometry (Eds. Tölke, J. and Wills, J. M.), Proc. Geom. Sympos. (Siegen, 1978), 226–237, Birkhäuser, Basel, 1979.Google Scholar
[BHW] Bokowski, J., Hadwiger, H. and Wills, J. M., Eine Ungleichung zwischen Volumen, Oberfläche und Gitterpunktanzahl konvexer Körper im n-dimensionalen euklidischen Raum. Math. Z. 127 (1972), 363–364.Google Scholar
[BF] Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper Springer, Berlin, 1934.Google Scholar
[C] Cassels, J. W. S., An introduction to Diophantine Approximation. Cambridge University Press, London, 1965.Google Scholar
[DR] Diaz, R. and Robins, S., The Ehrhardt polynomial of a lattice n-simplex. Electron. Res. Announc. Amer. Math. Soc. (1) 2 (1996).Google Scholar
[F] Federer, H., Geometric measure theory Springer, Berlin, 1969.Google Scholar
[GL] Gruber, P. M. and Lekkerkerker, C. G., Geometry of Numbers. North Holland, Amsterdam 1987.Google Scholar
[GW] Gritzmann, P. and Wills, J. M., Finite packing and covering. Chapter 3.4 in: Handbook of Convex Geometry (Eds. Gruber, P. M. and Wills, J. M.), North Holland, Amsterdam 1993.Google Scholar
[KN] Krätzel, E. and Nowak, W. G., Lattice points in large convex bodies, II. Acta Arith. 62 (1992), 285–295.Google Scholar
[MN] Müller, W. and Nowak, W. G., Lattice Points in Planar Domains. Lecture Notes in Math. 1452 (1990), 139–164.Google Scholar
[P] Pinkus, A., n-Widths in Approximation Theory. Springer-Verlag, Berlin, 1985.Google Scholar
[S] Schneider, R., Convex Bodies—the Brunn-Minkowski theory. Cambridge University Press, Cambridge, 1993.Google Scholar
[Sc] Schneider, T., Einführung in die transzendenten Zahlen Springer, Berlin, 1957.Google Scholar