Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-10T03:00:20.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Apolar Schemes of Algebraic Forms

Published online by Cambridge University Press:  20 November 2018

Jaydeep Chipalkatti
Jaydeep Chipalkatti*
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, MB, R3T 2N2 e-mail: chipalka@cc.umanitoba.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This is a note on the classical Waring's problem for algebraic forms. Fix integers 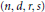$(n,d,r,s)$, and let 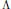$\Lambda $ be a general $r$-dimensional subspace of degree $d$ homogeneous polynomials in 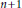$n+1$ variables. Let 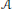$\mathcal{A}$ denote the variety of $s$-sided polar polyhedra of 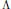$\Lambda $. We carry out a case-by-case study of the structure of 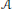$\mathcal{A}$ for several specific values of 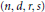$(n,d,r,s)$. In the first batch of examples, 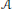$\mathcal{A}$ is shown to be a rational variety. In the second batch, 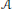$\mathcal{A}$ is a finite set of which we calculate the cardinality.

Keywords

14N0514N15Waring's problemapolaritypolar polyhedron
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 3 , 01 June 2006 , pp. 476 - 491
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of Algebraic Curves, Volume I. Grundlehren der math. Wissenschaften 267, Springer-Verlag, New York, 1985.Google Scholar
[2] Carlini, E. and Chipalkatti, J., On Waring's problem for several algebraic forms. Comment. Math. Helv. 78(2003), no. 3, 494–517.Google Scholar
[3] Ciliberto, C., Geramita, A. V. and Orecchia, F., Remarks on a theorem of Hilbert–Burch. Boll. Un. Mat. Ital. B (7) 2(1988), no. 3, 463–483.Google Scholar
[4] Dionisi, C. and Fontanari, C., Grassmann defectivity à la Terracini. Le Matematiche, to appear.Google Scholar
[5] Dolgachev, I., On certain families of elliptic curves in projective space. Ann. Mat. Pura Appl. 183(2004), no. 3, 317–331.Google Scholar
[6] Dolgachev, I. and Kanev, V., Polar covariants of cubics and quartics. Adv. in Math. 98(1993), no. 2, 216–301.Google Scholar
[7] Ehrenborg, R. and Rota, G.-C., Apolarity and canonical forms for homogeneous polynomials. European J. Combin. (3) 14(1993), 157–181.Google Scholar
[8] Eisenbud, D., Commutative Algebra, with a View Toward Algebraic Geometry. Graduate Texts in Math., Springer-Verlag, New York, 1995.Google Scholar
[9] Eisenbud, D., Green, M. and Harris, J., Cayley-Bacharach theorems and conjectures. Bull. Amer. Math. Soc. N.S. 33(1996), no. 3, 295–324.Google Scholar
[10] Ellingsrud, G. and Strømme, S. A., The number of twisted cubic curves on a quintic threefold. Math. Scand. 76(1995), no. 1, 5–34.Google Scholar
[11] Fontanari, C., On Waring's problem for many forms and Grassmann defective varieties. J. Pure Appl. Algebra 74(2002), no. 3, 243–247.Google Scholar
[12] Fulton, W., Intersection Theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, 3 Folge. Springer-Verlag, Berlin, 2nd edition, 1998.Google Scholar
[13] Fulton, W. and Harris, J., Representation Theory, A First Course. Graduate Texts in Math., Springer-Verlag, New York, 1991.Google Scholar
[14] Geramita, A. V., Inverse Systems of Fat Points. Queen's Papers in Pure and Applied Math. X, Queen's University, 1995.Google Scholar
[15] Griffiths, P. A. and Harris, J., Principles of Algebraic Geometry. Wiley Interscience, New York, 1978.Google Scholar
[16] Harris, J., Algebraic Geometry, A First Course. Graduate Texts in Math., Springer-Verlag, New York, 1992.Google Scholar
[17] Hartshorne, R., Algebraic Geometry. Graduate Texts in Math., Springer-Verlag, New York, 1977.Google Scholar
[18] Iarrobino, A., Inverse system of a symbolic power II. The Waring problem for forms. J. Algebra 174(1995), no. 3, 1091–1110.Google Scholar
[19] Iarrobino, A. and Kanev, V., Power Sums, Gorenstein Algebras and Determinantal Loci. Springer Lecture Notes in Math. 1721, 1999.Google Scholar
[20] Lakatos, I., Proofs and Refutations. Cambridge University Press, 1976.Google Scholar
[21] London, F., Über die Polarfiguren der ebenen Curven dritter Ordnung. Math. Ann. 36(1890), 535–584.Google Scholar
[22] Ranestad, K. and Schreyer, F.-O., Varieties of sums of powers. J. Reine Angew. Math. 525(2000), 147–181.Google Scholar
[23] Reichstein, B. and Reichstein, Z., Surfaces parametrizing Waring presentation of smooth plane cubics. Michigan Math. J. 40(1993), 95–118.Google Scholar
[24] Room, T. G., The Geometry of Determinantal Loci. Cambridge University Press, Cambridge, 1938.Google Scholar
[25] Schlesinger, O., Ueber die Verwerthung der ϑ-Functionen . Math. Ann. 31(1888), 183–219.Google Scholar
[26] Terracini, A., Sulla rappresentazione delle coppie di forme ternarie mediante somme di potenze di forme lineari. Ann. Mat. Serie III XXIV(1915).Google Scholar