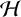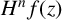Let $\mathcal {H}$ be the class of all analytic self-maps of the open unit disk $\mathbb {D}$. Denote by $H^n f(z)$ the nth-order hyperbolic derivative of 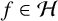$f\in \mathcal H$ at 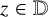$z\in \mathbb {D}$. We develop a method allowing us to calculate higher-order hyperbolic derivatives in an expeditious manner. We also generalise certain classical results for variability regions of the nth derivative of bounded analytic functions. For 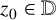$z_0\in \mathbb {D}$ and $\gamma = (\gamma _0, \gamma _1 , \ldots , \gamma _{n-1}) \in {\mathbb D}^{n}$, let 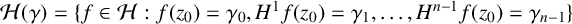${\mathcal H} (\gamma ) = \{f \in {\mathcal H} : f (z_0) = \gamma _0,H^1f (z_0) = \gamma _1,\ldots ,H^{n-1}f (z_0) = \gamma _{n-1} \}$. We determine the variability region $\{ f^{(n)}(z_0) : f \in {\mathcal H} (\gamma ) \}$ to prove a Schwarz–Pick lemma for the nth derivative. We apply this result to establish an nth-order Dieudonné lemma, which provides an explicit description of the variability region 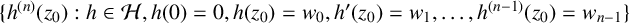$\{h^{(n)}(z_0): h\in \mathcal {H}, h(0)=0,h(z_0) =w_0, h'(z_0)=w_1,\ldots , h^{(n-1)}(z_0)=w_{n-1}\}$ for given 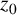$z_0$, 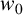$w_0$, $w_1,\ldots ,w_{n-1}$. Moreover, we determine the form of all extremal functions.