We explore transversals of finite index subgroups of finitely generated groups. We show that when 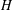$H$ is a subgroup of a rank-$n$ group 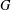$G$ and 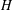$H$ has index at least $n$ in 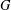$G$, we can construct a left transversal for $H$ which contains a generating set of size $n$ for 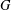$G$; this construction is algorithmic when $G$ is finitely presented. We also show that, in the case where $G$ has rank 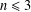$n\leq 3$, there is a simultaneous left–right transversal for 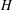$H$ which contains a generating set of size $n$ for 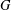$G$. We finish by showing that if 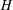$H$ is a subgroup of a rank-$n$ group 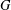$G$ with index less than 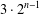$3\cdot 2^{n-1}$, and 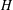$H$ contains no primitive elements of 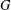$G$, then 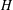$H$ is normal in 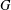$G$ and 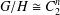$G/H\cong C_{2}^{n}$.