Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-06T20:24:18.440Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSFORMATION FORMULAS FOR THE NUMBER OF REPRESENTATIONS OF $n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS

Part of: Series expansions Diophantine equations Forms and linear algebraic groups Other special functions

Published online by Cambridge University Press:  08 January 2020

ZHI-HONG SUN Open the ORCID record for ZHI-HONG SUN [Opens in a new window]
ZHI-HONG SUN*
Affiliation:
School of Mathematics and Statistics,Huaiyin Normal University, Huaian, Jiangsu 223300, PR China email zhsun@hytc.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\mathbb{Z}$ and $\mathbb{Z}^{+}$ be the set of integers and the set of positive integers, respectively. For 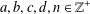$a,b,c,d,n\in \mathbb{Z}^{+}$, let 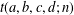$t(a,b,c,d;n)$ be the number of representations of $n$ by $\frac{1}{2}ax(x+1)+\frac{1}{2}by(y+1)+\frac{1}{2}cz(z+1)+\frac{1}{2}dw(w+1)$ with 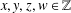$x,y,z,w\in \mathbb{Z}$. Using theta function identities we prove 13 transformation formulas for 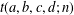$t(a,b,c,d;n)$ and evaluate 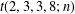$t(2,3,3,8;n)$, 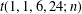$t(1,1,6,24;n)$ and 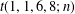$t(1,1,6,8;n)$.

Keywords

theta functiontriangular numberquadratic form

MSC classification

Primary: 11D85: Representation problems
Secondary: 11E20: General ternary and quaternary quadratic forms; forms of more than two variables 11E25: Sums of squares and representations by other particular quadratic forms 30B10: Power series (including lacunary series) 33E20: Other functions defined by series and integrals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 39 - 49
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

The author is supported by the National Natural Science Foundation of China (Grant No. 11771173).

References

Adiga, C., Cooper, S. and Han, J. H., ‘A general relation between sums of squares and sums of triangular numbers’, Int. J. Number Theory 1 (2005), 175–182.CrossRefGoogle Scholar
Baruah, N. D., Cooper, S. and Hirschhorn, M., ‘Sums of squares and sums of triangular numbers induced by partitions of 8’, Int. J. Number Theory 4 (2008), 525–538.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).CrossRefGoogle Scholar
Cooper, S., ‘On the number of representations of integers by certain quadratic forms, II’, J. Comb. Number Theory 1 (2009), 153–182.Google Scholar
Dickson, L. E., History of the Theory of Numbers, Vol. III (Carnegie Institute of Washington, Washington, DC, 1923), reprinted by Chelsea, New York, 1999.Google Scholar
Sun, Z.-H., ‘Some relations between t (a, b, c, d; n) and N (a, b, c, d; n)’, Acta Arith. 175 (2016), 269–289.Google Scholar
Sun, Z.-H., ‘The number of representations of n as a linear combination of triangular numbers’, Int. J. Number Theory 15 (2019), 1191–1218.CrossRefGoogle Scholar
Wang, M. and Sun, Z.-H., ‘On the number of representations of n as a linear combination of four triangular numbers’, Int. J. Number Theory 12 (2016), 1641–1662.CrossRefGoogle Scholar
Wang, M. and Sun, Z.-H., ‘On the number of representations of n as a linear combination of four triangular numbers II’, Int. J. Number Theory 13 (2017), 593–617.CrossRefGoogle Scholar
Williams, K. S., ‘n =𝛥 +𝛥 + 2(𝛥+𝛥)’, Far East J. Math. Sci. 11 (2003), 233–240.Google Scholar
Williams, K. S., Number Theory in the Spirit of Liouville (Cambridge University Press, New York, 2011).Google Scholar