Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-09T15:01:16.032Z Has data issue: false hasContentIssue false
  • English
  • Français

TOEPLITZ OPERATORS BETWEEN FOCK SPACES

Part of: Holomorphic functions of several complex variables Special classes of linear operators

Published online by Cambridge University Press:  02 June 2015

JIN LU  and
XIAOFEN LV
JIN LU
Affiliation:
Department of Mathematics, Huzhou University, Huzhou, Zhejiang 313000, PR China email lujin@mail.ustc.edu.cn
XIAOFEN LV*
Affiliation:
Department of Mathematics, Huzhou University, Huzhou, Zhejiang 313000, PR China email lvxf@hutc.zj.cn
*
✉lvxf@hutc.zj.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a positive Borel measure ${\it\mu}$ on the $n$-dimensional Euclidean space $\mathbb{C}^{n}$, we characterise the boundedness (and compactness) of Toeplitz operators 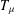$T_{{\it\mu}}$ between Fock spaces 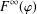$F^{\infty }({\it\varphi})$ and 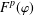$F^{p}({\it\varphi})$ with $0<p\leq \infty$ in terms of $t$-Berezin transforms and averaging functions of ${\it\mu}$. Our result extends recent work of Mengestie [‘On Toeplitz operators between Fock spaces’, Integral Equations Operator Theory78 (2014), 213–224] and others.

Keywords

Toeplitz operatorFock spacet-Berezin transforms

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 32A36: Bergman spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 316 - 324
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bauer, W., Coburn, L. and Isralowitz, J., ‘Heat flow, BMO, and the compactness of Toeplitz operators’, J. Funct. Anal. 259 (2010), 57–78.CrossRefGoogle Scholar
Hu, Z. J. and Lv, X. F., ‘Toeplitz operators from one Fock space to another’, Integral Equations Operator Theory 70 (2011), 541–559.CrossRefGoogle Scholar
Hu, Z. J. and Lv, X. F., ‘Toeplitz operators on Fock spaces F p(𝜙)’, Integral Equations Operator Theory 80(1) (2014), 33–59.CrossRefGoogle Scholar
Isralowitz, J. and Zhu, K. H., ‘Toeplitz operators on the Fock space’, Integral Equations Operator Theory 66(4) (2010), 593–611.CrossRefGoogle Scholar
Mengestie, T., ‘On Toeplitz operators between Fock spaces’, Integral Equations Operator Theory 78 (2014), 213–224.CrossRefGoogle Scholar
Schuster, A. and Varolin, D., ‘Toeplitz operators and Carleson measures on generalized Bargmann–Fock spaces’, Integral Equations Operator Theory 72(3) (2012), 363–392.CrossRefGoogle Scholar
Zhu, K. H., Analysis on Fock Spaces, Graduate Texts in Mathematics, 263 (Springer, New York, 2012).CrossRefGoogle Scholar