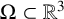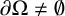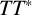1 Introduction
1.1 The cylindrical model problem
Let
![]() $\Omega =\{x\geq 0,(y,z)\in \mathbb {R}^2\}\subset \mathbb {R}^3$
with smooth boundary
$\Omega =\{x\geq 0,(y,z)\in \mathbb {R}^2\}\subset \mathbb {R}^3$
with smooth boundary
![]() $\partial \Omega =\{x=0\}$
and let
$\partial \Omega =\{x=0\}$
and let
![]() $\Delta =\partial _x^2+(1+x)\partial _y^2+\partial _z^2$
. We consider solutions of the linear Dirichlet wave equation inside
$\Delta =\partial _x^2+(1+x)\partial _y^2+\partial _z^2$
. We consider solutions of the linear Dirichlet wave equation inside
![]() $\Omega $
:
$\Omega $
:
The Riemannian manifold
![]() $(\Omega ,\Delta )$
with
$(\Omega ,\Delta )$
with
![]() $\Delta =\partial _x^2+(1+x)\partial _y^2+\partial _z^2$
can be locally seen as a cylindrical domain in
$\Delta =\partial _x^2+(1+x)\partial _y^2+\partial _z^2$
can be locally seen as a cylindrical domain in
![]() $\mathbb {R}^3$
by taking cylindrical coordinates
$\mathbb {R}^3$
by taking cylindrical coordinates
![]() $(r,\theta ,z)$
, where we set
$(r,\theta ,z)$
, where we set
![]() $r=1-x/2,\theta =y$
and
$r=1-x/2,\theta =y$
and
![]() $z=z$
. The main goal of this work is to prove the Strichartz estimates inside cylindrical convex domains for the solution u to (1.1).
$z=z$
. The main goal of this work is to prove the Strichartz estimates inside cylindrical convex domains for the solution u to (1.1).
1.2 Some known results
Let us recall a few results about Strichartz estimates (see [Reference Ivanovici, Lebeau and Planchon10, Section 1]). Let
![]() $(\Omega ,g)$
be a Riemannian manifold without boundary of dimension
$(\Omega ,g)$
be a Riemannian manifold without boundary of dimension
![]() $d\geq 2$
. Local-in-time Strichartz estimates state that
$d\geq 2$
. Local-in-time Strichartz estimates state that
where
![]() $\dot {H}^\beta $
denotes the homogeneous Sobolev space over
$\dot {H}^\beta $
denotes the homogeneous Sobolev space over
![]() $\Omega $
of order
$\Omega $
of order
![]() $\beta $
,
$\beta $
,
![]() $2\leq q,r\leq \infty $
and
$2\leq q,r\leq \infty $
and
 $$ \begin{align*} \frac{1}{q}+\frac{d}{r}=\frac{d}{2}-\beta,\quad \frac{1}{q}\leq \frac{d-1}{2}\bigg(\frac{1}{2}-\frac{1}{r}\bigg). \end{align*} $$
$$ \begin{align*} \frac{1}{q}+\frac{d}{r}=\frac{d}{2}-\beta,\quad \frac{1}{q}\leq \frac{d-1}{2}\bigg(\frac{1}{2}-\frac{1}{r}\bigg). \end{align*} $$
Here
![]() $u=u(t,x)$
is a solution to the wave equation
$u=u(t,x)$
is a solution to the wave equation
where
![]() $\Delta _g$
denotes the Laplace–Beltrami operator on
$\Delta _g$
denotes the Laplace–Beltrami operator on
![]() $(\Omega ,g)$
. The estimates (1.2) hold on
$(\Omega ,g)$
. The estimates (1.2) hold on
![]() $\Omega =\mathbb {R}^d$
and
$\Omega =\mathbb {R}^d$
and
![]() $g_{ij}=\delta _{ij}.$
$g_{ij}=\delta _{ij}.$
Blair et al. [Reference Blair, Smith and Sogge4] proved the Strichartz estimates for the wave equation on a (compact or noncompact) Riemannian manifold with boundary. They proved that the Strichartz estimates (1.2) hold if
![]() $\Omega $
is a compact manifold with boundary and
$\Omega $
is a compact manifold with boundary and
![]() $ (q,r,\beta )$
is a triple satisfying
$ (q,r,\beta )$
is a triple satisfying
 $$ \begin{align*} \frac{1}{q}+\frac{d}{r}=\frac{d}{2}-\beta \quad \text{for } \begin{cases} \dfrac{3}{q}+\dfrac{d-1}{r}\leq\dfrac{d-1}{2},\quad d\leq 4,\\[0.3 cm] \dfrac{1}{q}+\dfrac{1}{r}\leq \dfrac{1}{2},\quad d\geq 4. \end{cases} \end{align*} $$
$$ \begin{align*} \frac{1}{q}+\frac{d}{r}=\frac{d}{2}-\beta \quad \text{for } \begin{cases} \dfrac{3}{q}+\dfrac{d-1}{r}\leq\dfrac{d-1}{2},\quad d\leq 4,\\[0.3 cm] \dfrac{1}{q}+\dfrac{1}{r}\leq \dfrac{1}{2},\quad d\geq 4. \end{cases} \end{align*} $$
Recently in [Reference Ivanovici, Lebeau and Planchon10], Ivanovici et al. deduced local-in-time Strichartz estimates (1.2) from the optimal dispersive estimates inside strictly convex domains of dimension
![]() $d\geq 2$
for a triple
$d\geq 2$
for a triple
![]() $(d,q,\beta )$
satisfying
$(d,q,\beta )$
satisfying
 $$ \begin{align*} \frac{1}{q}\leq\bigg(\frac{d-1}{2}-\frac{1}{4}\bigg)\bigg(\frac{1}{2}-\frac{1}{r}\bigg) \quad \text{and}\quad \beta=d\bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}. \end{align*} $$
$$ \begin{align*} \frac{1}{q}\leq\bigg(\frac{d-1}{2}-\frac{1}{4}\bigg)\bigg(\frac{1}{2}-\frac{1}{r}\bigg) \quad \text{and}\quad \beta=d\bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}. \end{align*} $$
For
![]() $d\geq 3$
, this improves the range of indices for which sharp Strichartz estimates hold compared to the result by Blair et al. [Reference Blair, Smith and Sogge4]. However, the results in [Reference Blair, Smith and Sogge4] apply to any domains or manifolds with boundary. The latest results in [Reference Ivanovici, Lebeau and Planchon11] on Strichartz estimates inside the Friedlander model domain have been obtained for pairs
$d\geq 3$
, this improves the range of indices for which sharp Strichartz estimates hold compared to the result by Blair et al. [Reference Blair, Smith and Sogge4]. However, the results in [Reference Blair, Smith and Sogge4] apply to any domains or manifolds with boundary. The latest results in [Reference Ivanovici, Lebeau and Planchon11] on Strichartz estimates inside the Friedlander model domain have been obtained for pairs
![]() $(q, r)$
such that
$(q, r)$
such that
 $$ \begin{align*}\frac{1}{q}\leq \bigg(\frac{1}{2}-\frac{1}{9}\bigg)\bigg(\frac{1}{2}-\frac{1}{r}\bigg).\end{align*} $$
$$ \begin{align*}\frac{1}{q}\leq \bigg(\frac{1}{2}-\frac{1}{9}\bigg)\bigg(\frac{1}{2}-\frac{1}{r}\bigg).\end{align*} $$
This result improves on the known results for strictly convex domains for
![]() $d=2$
, while [Reference Ivanovici, Lebeau and Planchon10] only gives a loss of
$d=2$
, while [Reference Ivanovici, Lebeau and Planchon10] only gives a loss of
![]() $\tfrac 14$
.
$\tfrac 14$
.
Let us also recall that dispersive estimates for the wave equation in
![]() $\mathbb {R}^ d$
follow from the representation of the solution as a sum of Fourier integral operators (see [Reference Bahouri, Chemin and Danchin1, Reference Brener5, Reference Ginibre and Velo8]). They read as follows:
$\mathbb {R}^ d$
follow from the representation of the solution as a sum of Fourier integral operators (see [Reference Bahouri, Chemin and Danchin1, Reference Brener5, Reference Ginibre and Velo8]). They read as follows:
 $$ \begin{align} \|\,\chi(hD_t)e^{\pm it\sqrt{-\Delta_{\mathbb{R}^d}}}\|_{L^1(\mathbb{R}^ d)\rightarrow L^\infty(\mathbb{R}^ d)}\leq Ch^{-d}\min\bigg\{1,\bigg(\frac{h}{|t|}\bigg)^{{(d-1)}/{2}}\bigg\}, \end{align} $$
$$ \begin{align} \|\,\chi(hD_t)e^{\pm it\sqrt{-\Delta_{\mathbb{R}^d}}}\|_{L^1(\mathbb{R}^ d)\rightarrow L^\infty(\mathbb{R}^ d)}\leq Ch^{-d}\min\bigg\{1,\bigg(\frac{h}{|t|}\bigg)^{{(d-1)}/{2}}\bigg\}, \end{align} $$
where
![]() $\Delta _{\mathbb {R}^d}$
is the Laplace operator in
$\Delta _{\mathbb {R}^d}$
is the Laplace operator in
![]() $\mathbb {R}^d$
. Here and in the following, the function
$\mathbb {R}^d$
. Here and in the following, the function
![]() $\chi $
belongs to
$\chi $
belongs to
![]() $C_0^\infty (]0,\infty [)$
and is equal to
$C_0^\infty (]0,\infty [)$
and is equal to
![]() $1$
on
$1$
on
![]() $[1,2]$
and
$[1,2]$
and
![]() $D_t={(1}/{i})\partial _t$
. Inside strictly convex domains
$D_t={(1}/{i})\partial _t$
. Inside strictly convex domains
![]() $\Omega _D$
of dimensions
$\Omega _D$
of dimensions
![]() $d\geq 2$
, the optimal (local-in-time) dispersive estimates for the wave equation have been established by Ivanovici et al. [Reference Ivanovici, Lebeau and Planchon10]. More precisely, they have proved that
$d\geq 2$
, the optimal (local-in-time) dispersive estimates for the wave equation have been established by Ivanovici et al. [Reference Ivanovici, Lebeau and Planchon10]. More precisely, they have proved that
 $$ \begin{align} \|\,\chi(hD_t)e^{\pm it\sqrt{-\Delta_D}}\|_{L^1(\Omega_D)\rightarrow L^\infty(\Omega_D)}\leq Ch^{-d}\min\bigg\{1,\bigg(\frac{h}{|t|}\bigg)^{{(d-1)}/{2}-{1}/{4}}\bigg\}, \end{align} $$
$$ \begin{align} \|\,\chi(hD_t)e^{\pm it\sqrt{-\Delta_D}}\|_{L^1(\Omega_D)\rightarrow L^\infty(\Omega_D)}\leq Ch^{-d}\min\bigg\{1,\bigg(\frac{h}{|t|}\bigg)^{{(d-1)}/{2}-{1}/{4}}\bigg\}, \end{align} $$
where
![]() $\Delta _D$
is the Laplace operator on
$\Delta _D$
is the Laplace operator on
![]() $\Omega _D$
. Due to the formation of caustics in arbitrarily small times, (1.4) induces a loss of
$\Omega _D$
. Due to the formation of caustics in arbitrarily small times, (1.4) induces a loss of
![]() $\tfrac 14$
powers of the
$\tfrac 14$
powers of the
![]() $(h/|t|)$
factor compared to (1.3). The local-in-time dispersive estimates for the wave equation inside cylindrical convex domains in dimension
$(h/|t|)$
factor compared to (1.3). The local-in-time dispersive estimates for the wave equation inside cylindrical convex domains in dimension
![]() $3$
have been derived in [Reference Meas13, Reference Meas14] as follows:
$3$
have been derived in [Reference Meas13, Reference Meas14] as follows:
 $$ \begin{align*} \|\,\chi(hD_t)\mathcal{G}_a(t,x,y,z)\|_{L^1(\Omega)\rightarrow L^\infty(\Omega)}\leq Ch^{-3}\min\bigg\{1,\bigg(\frac{h}{|t|}\bigg)^{{3}/{4}}\bigg\}, \end{align*} $$
$$ \begin{align*} \|\,\chi(hD_t)\mathcal{G}_a(t,x,y,z)\|_{L^1(\Omega)\rightarrow L^\infty(\Omega)}\leq Ch^{-3}\min\bigg\{1,\bigg(\frac{h}{|t|}\bigg)^{{3}/{4}}\bigg\}, \end{align*} $$
where
![]() $\mathcal {G}_a$
is the Green function for (1.1).
$\mathcal {G}_a$
is the Green function for (1.1).
2 Main result
We now state our main result concerning the Strichartz estimates inside cylindrical convex domains in dimension
![]() $3$
.
$3$
.
Theorem 2.1. Let
![]() $(\Omega ,\Delta )$
be defined as before. Let u be a solution of the wave equation on
$(\Omega ,\Delta )$
be defined as before. Let u be a solution of the wave equation on
![]() $\Omega $
:
$\Omega $
:
Then for all T, there exists
![]() $C_T$
such that
$C_T$
such that
with
 $$ \begin{align*} \frac{1}{q}\leq \frac{3}{4}\bigg(\frac{1}{2}-\frac{1}{r}\bigg) \quad \text{and}\quad \beta=3\bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}. \end{align*} $$
$$ \begin{align*} \frac{1}{q}\leq \frac{3}{4}\bigg(\frac{1}{2}-\frac{1}{r}\bigg) \quad \text{and}\quad \beta=3\bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}. \end{align*} $$
To prove Theorem 2.1, we first prove the frequency-localised Strichartz estimates by utilising the frequency-localised dispersive estimates, interpolation and
![]() $TT^\ast $
arguments. We then apply the Littlewood–Paley square function estimates (see [Reference Blair, Ford, Herr and Marzuola2, Reference Blair, Ford and Marzuola3, Reference Ivanovici and Planchon12]) to get the Strichartz estimates (Theorem 2.1) in the context of cylindrical domains. For
$TT^\ast $
arguments. We then apply the Littlewood–Paley square function estimates (see [Reference Blair, Ford, Herr and Marzuola2, Reference Blair, Ford and Marzuola3, Reference Ivanovici and Planchon12]) to get the Strichartz estimates (Theorem 2.1) in the context of cylindrical domains. For
![]() $d=3$
, Theorem 2.1 improves the range of indices for which the sharp Strichartz estimates hold. However, our result is restricted to cylindrical domains, while [Reference Blair, Smith and Sogge4] applies to any domain.
$d=3$
, Theorem 2.1 improves the range of indices for which the sharp Strichartz estimates hold. However, our result is restricted to cylindrical domains, while [Reference Blair, Smith and Sogge4] applies to any domain.
3 Strichartz estimates for the model problem
Let us recall some notation. For any
![]() $I\subset \mathbb {R},\Omega \subset \mathbb {R}^d$
, we define the mixed space-time norms
$I\subset \mathbb {R},\Omega \subset \mathbb {R}^d$
, we define the mixed space-time norms
 $$ \begin{align*} \|u\|_{L^q(I;L^r(\Omega))}&:=\bigg(\int_I\|u(t,.)\|_{L^r(\Omega)}^q\,dt\bigg)^{1/q}\quad\text{if } 1\leq q<\infty,\\ \|u\|_{L^{\infty}(I;L^r(\Omega))}&:=\mathop{\mathrm{ess\, sup}}_{t\in I}\|u(t,.)\|_{L^r(\Omega)}. \end{align*} $$
$$ \begin{align*} \|u\|_{L^q(I;L^r(\Omega))}&:=\bigg(\int_I\|u(t,.)\|_{L^r(\Omega)}^q\,dt\bigg)^{1/q}\quad\text{if } 1\leq q<\infty,\\ \|u\|_{L^{\infty}(I;L^r(\Omega))}&:=\mathop{\mathrm{ess\, sup}}_{t\in I}\|u(t,.)\|_{L^r(\Omega)}. \end{align*} $$
3.1 Frequency-localised Strichartz estimates
In this section, we prove Theorem 3.1. The classical strategy is as follows. We begin by interpolating between the energy estimates and dispersive estimates. This yields a new estimate, which we further manipulate via a classical
![]() $L^p$
inequality to establish (3.8). This last step imposes conditions on the space-time exponent pair
$L^p$
inequality to establish (3.8). This last step imposes conditions on the space-time exponent pair
![]() $(q,r)$
; these are precisely the wave admissibility criteria. The classical inequalities used are the Young, Hölder and Hardy–Littlewood–Sobolev inequalities.
$(q,r)$
; these are precisely the wave admissibility criteria. The classical inequalities used are the Young, Hölder and Hardy–Littlewood–Sobolev inequalities.
We first recall the Littlewood–Paley decomposition and some links with Sobolev spaces [Reference Bahouri, Chemin and Danchin1]. Let
![]() $\chi \in C_0^\infty (\mathbb {R}^*)$
and equal to
$\chi \in C_0^\infty (\mathbb {R}^*)$
and equal to
![]() $1$
on
$1$
on
![]() $[\tfrac 12,2]$
such that
$[\tfrac 12,2]$
such that
 $$ \begin{align*} \sum_{j\in\mathbb{Z}}\chi(2^{-j}\lambda)=1,\quad \lambda>0. \end{align*} $$
$$ \begin{align*} \sum_{j\in\mathbb{Z}}\chi(2^{-j}\lambda)=1,\quad \lambda>0. \end{align*} $$
We define the associated Littlewood–Paley frequency cutoffs
![]() $\chi (2^{-j}\sqrt {-\Delta })$
using the spectral theorem for
$\chi (2^{-j}\sqrt {-\Delta })$
using the spectral theorem for
![]() $\Delta $
and we have
$\Delta $
and we have
 $$ \begin{align*} \sum_{j\in\mathbb{Z}}\chi(2^{-j}\sqrt{-\Delta})=\mbox{Id}: L^2(\Omega)\longrightarrow L^2(\Omega). \end{align*} $$
$$ \begin{align*} \sum_{j\in\mathbb{Z}}\chi(2^{-j}\sqrt{-\Delta})=\mbox{Id}: L^2(\Omega)\longrightarrow L^2(\Omega). \end{align*} $$
This decomposition takes a single function and writes it as a superposition of a countably infinite family of functions
![]() $\chi $
each one having a frequency of magnitude
$\chi $
each one having a frequency of magnitude
![]() $\sim 2^{j}$
for
$\sim 2^{j}$
for
![]() $j\geq 1$
. A norm of the homogeneous Sobolev space
$j\geq 1$
. A norm of the homogeneous Sobolev space
![]() $\dot {H}^{\beta }$
is defined as follows: for all
$\dot {H}^{\beta }$
is defined as follows: for all
![]() $\beta \geq 0$
,
$\beta \geq 0$
,
 $$ \begin{align*} \|u\|_{\dot{H}^\beta}:=\bigg(\sum_{j\in\mathbb{Z}}2^{2j\beta}\|\chi(2^{-j}D_t)u\|_{L^2}^2\bigg)^{1/2}. \end{align*} $$
$$ \begin{align*} \|u\|_{\dot{H}^\beta}:=\bigg(\sum_{j\in\mathbb{Z}}2^{2j\beta}\|\chi(2^{-j}D_t)u\|_{L^2}^2\bigg)^{1/2}. \end{align*} $$
With this decomposition, the Littlewood–Paley square function estimate (see [Reference Blair, Ford, Herr and Marzuola2, Reference Blair, Ford and Marzuola3, Reference Ivanovici and Planchon12]) reads as follows: for
![]() $f\in L^r(\Omega )$
and for all
$f\in L^r(\Omega )$
and for all
![]() $r\in [2,\infty [$
,
$r\in [2,\infty [$
,
 $$ \begin{align} \|f\|_{L^r(\Omega)}\leq C_r\bigg\|\bigg(\sum_{j\in\mathbb{Z}}|\chi(2^{-j}\sqrt{-\Delta})f|^2\bigg)^{1/2}\bigg\|_{L^r(\Omega)}. \end{align} $$
$$ \begin{align} \|f\|_{L^r(\Omega)}\leq C_r\bigg\|\bigg(\sum_{j\in\mathbb{Z}}|\chi(2^{-j}\sqrt{-\Delta})f|^2\bigg)^{1/2}\bigg\|_{L^r(\Omega)}. \end{align} $$
The proof follows from the classical Stein argument involving Rademacher functions and an appropriate Mikhlin–Hörmander multiplier theorem.
We define the frequency localisation
![]() $v_j$
of u by
$v_j$
of u by
![]() $v_j=\chi (2^{-j}\sqrt {-\Delta })u$
. Hence,
$v_j=\chi (2^{-j}\sqrt {-\Delta })u$
. Hence,
![]() $u=\sum _{j\geq 0}v_j$
. Let
$u=\sum _{j\geq 0}v_j$
. Let
![]() $h=2^{-j}$
. We deduce from the dispersive estimates inside cylindrical convex domains established in [Reference Meas13, Reference Meas14] the frequency-localised dispersive estimates for the solution
$h=2^{-j}$
. We deduce from the dispersive estimates inside cylindrical convex domains established in [Reference Meas13, Reference Meas14] the frequency-localised dispersive estimates for the solution
![]() $v_j=\chi (hD_t)u$
of the (frequency-localised) wave equation
$v_j=\chi (hD_t)u$
of the (frequency-localised) wave equation
which read as follows:
 $$ \begin{align} \|\dot{\mathcal U}(t)\chi(hD_t)u_0\|_{L^\infty}\lesssim h^{-3}\min\bigg\{1,\bigg(\frac{h}{t}\bigg)^{{3}/{4}}\bigg\}\|\chi(hD_t)\,u_0\|_{L^1},\\ \|\mathcal U(t)\chi(hD_t)u_1\|_{L^\infty}\lesssim h^{-2}\min\bigg\{1,\bigg(\frac{h}{t}\bigg)^{{3}/{4}}\bigg\}\|\chi(hD_t)\,u_1\|_{L^1},\nonumber \end{align} $$
$$ \begin{align} \|\dot{\mathcal U}(t)\chi(hD_t)u_0\|_{L^\infty}\lesssim h^{-3}\min\bigg\{1,\bigg(\frac{h}{t}\bigg)^{{3}/{4}}\bigg\}\|\chi(hD_t)\,u_0\|_{L^1},\\ \|\mathcal U(t)\chi(hD_t)u_1\|_{L^\infty}\lesssim h^{-2}\min\bigg\{1,\bigg(\frac{h}{t}\bigg)^{{3}/{4}}\bigg\}\|\chi(hD_t)\,u_1\|_{L^1},\nonumber \end{align} $$
where we use the notation
 $$ \begin{align*} \mathcal U(t):=\frac{\sin(t\sqrt{-\Delta})}{\sqrt{-\Delta}}& \quad\text{and}\quad \dot{\mathcal U}(t):=\cos(t\sqrt{-\Delta}). \end{align*} $$
$$ \begin{align*} \mathcal U(t):=\frac{\sin(t\sqrt{-\Delta})}{\sqrt{-\Delta}}& \quad\text{and}\quad \dot{\mathcal U}(t):=\cos(t\sqrt{-\Delta}). \end{align*} $$
These estimates yield the following Strichartz estimates.
Theorem 3.1 (Frequency-localised Strichartz estimates).
Let
![]() $(\Omega ,\Delta )$
be defined as before. Let
$(\Omega ,\Delta )$
be defined as before. Let
![]() $v_j$
be a solution of the (frequency-localised) wave equation (3.2). Then for all T, there exists
$v_j$
be a solution of the (frequency-localised) wave equation (3.2). Then for all T, there exists
![]() $C_T$
such that
$C_T$
such that
with
 $$ \begin{align*}q\in ]2,\infty],\quad r\in[2,\infty],\quad \frac{1}{q}\leq\alpha_3\bigg(\frac{1}{2}-\frac{1}{r}\bigg),\quad \alpha_3=\frac{3}{4},\quad \beta=3\bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}.\end{align*} $$
$$ \begin{align*}q\in ]2,\infty],\quad r\in[2,\infty],\quad \frac{1}{q}\leq\alpha_3\bigg(\frac{1}{2}-\frac{1}{r}\bigg),\quad \alpha_3=\frac{3}{4},\quad \beta=3\bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}.\end{align*} $$
Remark 3.2. If
![]() ${1}/{q}=\alpha _3({1}/{2}-{1}/{r})$
, then
${1}/{q}=\alpha _3({1}/{2}-{1}/{r})$
, then
![]() $\beta =(3-\alpha _3)({1}/{2}-{1}/{r})$
.
$\beta =(3-\alpha _3)({1}/{2}-{1}/{r})$
.
Proof of Theorem 3.1.
We prove only (3.4) since (3.5) follows analogously. We have the frequency-localised dispersive estimates in
![]() $\Omega $
in (3.3) for
$\Omega $
in (3.3) for
![]() $|t|\geq h$
,
$|t|\geq h$
,
and the energy estimates,
We apply the Riesz–Thorin interpolation theorem [Reference Hörmander9] to the operator
![]() $\dot {\mathcal {U}}(t)\chi (hD_t)$
for fixed time
$\dot {\mathcal {U}}(t)\chi (hD_t)$
for fixed time
![]() $t\in \mathbb {R}$
. Interpolating between (3.6) and (3.7) with
$t\in \mathbb {R}$
. Interpolating between (3.6) and (3.7) with
![]() $\theta =1-{2}/{r}$
yields
$\theta =1-{2}/{r}$
yields
for
![]() $2\leq r\leq \infty $
, where
$2\leq r\leq \infty $
, where
![]() $r'$
denotes the exponent conjugate to r (that is,
$r'$
denotes the exponent conjugate to r (that is,
![]() ${1}/{r}+{1}/{r'}=1$
). Let T be the operator solution defined by
${1}/{r}+{1}/{r'}=1$
). Let T be the operator solution defined by
Its adjoint is given by
Moreover,
By the
![]() $TT^*$
argument in [Reference Ginibre and Velo7], it is sufficient to prove
$TT^*$
argument in [Reference Ginibre and Velo7], it is sufficient to prove
We have
 $$ \begin{align} \| T^*T\psi\|_{L_t^qL_x^r}&=\bigg\|\int \dot{\mathcal U}(t-s)\chi^*(hD_t)\chi(hD_t)\psi(s) \,ds\bigg\|_{L_t^qL_x^r},\nonumber\\ &\lesssim h^{-2(3-\alpha_3)({1}/{2}-{1}/{r})}\bigg\|\int|t-s|^{-2\alpha_3({1}/{2}-{1}/{r})}\|\psi\|_ {L_x^{r'}}\,ds\bigg\|_{L_t^q}. \end{align} $$
$$ \begin{align} \| T^*T\psi\|_{L_t^qL_x^r}&=\bigg\|\int \dot{\mathcal U}(t-s)\chi^*(hD_t)\chi(hD_t)\psi(s) \,ds\bigg\|_{L_t^qL_x^r},\nonumber\\ &\lesssim h^{-2(3-\alpha_3)({1}/{2}-{1}/{r})}\bigg\|\int|t-s|^{-2\alpha_3({1}/{2}-{1}/{r})}\|\psi\|_ {L_x^{r'}}\,ds\bigg\|_{L_t^q}. \end{align} $$
When
![]() ${1}/{q}< \alpha _3({1}/{2}-{1}/{r})$
, we use Young’s inequality which states that
${1}/{q}< \alpha _3({1}/{2}-{1}/{r})$
, we use Young’s inequality which states that
where
![]() $1+{1}/{q}={1}/{\tilde r}+{1}/{p}$
. We apply (3.10) with
$1+{1}/{q}={1}/{\tilde r}+{1}/{p}$
. We apply (3.10) with
![]() $\tilde r=q/2, p=q'$
and
$\tilde r=q/2, p=q'$
and
![]() ${1}/{q}+{1}/{q'}=1$
to get the estimate
${1}/{q}+{1}/{q'}=1$
to get the estimate
 $$ \begin{align*} \bigg\|\int_ h^\infty|t-s|^{-2\alpha_3({1}/{2}-{1}/{r})}\|\psi\|_ {L_x^{r'}}\,ds\bigg\|_{L_t^q} & \leq \|\psi\|_{L_t^{q'}L_x^{r'}}\|t^{-2\alpha_3({1}/{2}-{1}/{r})}\|_{L_{|t|\geq h}^{q/2}} \\ & \leq h^{-2\alpha_3({1}{/2}-{1}/{r})+{2}/{q}}\| \psi\|_{L_t^{q'}L_x^{r'}}. \end{align*} $$
$$ \begin{align*} \bigg\|\int_ h^\infty|t-s|^{-2\alpha_3({1}/{2}-{1}/{r})}\|\psi\|_ {L_x^{r'}}\,ds\bigg\|_{L_t^q} & \leq \|\psi\|_{L_t^{q'}L_x^{r'}}\|t^{-2\alpha_3({1}/{2}-{1}/{r})}\|_{L_{|t|\geq h}^{q/2}} \\ & \leq h^{-2\alpha_3({1}{/2}-{1}/{r})+{2}/{q}}\| \psi\|_{L_t^{q'}L_x^{r'}}. \end{align*} $$
Since
![]() ${1}{/q}< \alpha _3({1}/{2}-{1}/{r})$
,
${1}{/q}< \alpha _3({1}/{2}-{1}/{r})$
,
 $$ \begin{align*} \|t^{-2\alpha_3({1}/{2}-{2}/{r})}\|_{L_{|t|\geq h}^{q/2}}=\bigg(\int_h^\infty t^{-2\alpha_3({1}/{2}-{2}/{r})q/2} \,dt\bigg)^{2/q}\simeq h^{-2\alpha_3({1}/{2}-{1}/{r})+{2}/{q}}. \end{align*} $$
$$ \begin{align*} \|t^{-2\alpha_3({1}/{2}-{2}/{r})}\|_{L_{|t|\geq h}^{q/2}}=\bigg(\int_h^\infty t^{-2\alpha_3({1}/{2}-{2}/{r})q/2} \,dt\bigg)^{2/q}\simeq h^{-2\alpha_3({1}/{2}-{1}/{r})+{2}/{q}}. \end{align*} $$
Then (3.9) becomes
 $$ \begin{align*} \| T^*T\psi\|_{L_t^qL_x^r} &\lesssim h^{-2(3-\alpha_3)({1}/{2}-{1}/{r})}\bigg\|\int|t-s|^{-2\alpha_3({1}/{2}-{1}/{r})}\|\psi\|_ {L_x^{r'}}\,ds\bigg\|_{L_t^q},\\ &\lesssim h^{-2[3({1}/{2}-{1}/{r})-\frac{1}{q}]}\| \psi\|_{L_t^{q'}L_x^{r'}} \lesssim h^{-2\beta}\| \psi\|_{L_t^{q'}L_x^{r'}}. \end{align*} $$
$$ \begin{align*} \| T^*T\psi\|_{L_t^qL_x^r} &\lesssim h^{-2(3-\alpha_3)({1}/{2}-{1}/{r})}\bigg\|\int|t-s|^{-2\alpha_3({1}/{2}-{1}/{r})}\|\psi\|_ {L_x^{r'}}\,ds\bigg\|_{L_t^q},\\ &\lesssim h^{-2[3({1}/{2}-{1}/{r})-\frac{1}{q}]}\| \psi\|_{L_t^{q'}L_x^{r'}} \lesssim h^{-2\beta}\| \psi\|_{L_t^{q'}L_x^{r'}}. \end{align*} $$
When
![]() ${1}/{q}= \alpha _3({1}/{2}-{1}/{r})$
, we instead use the Hardy–Littlewood–Sobolev inequality (see [Reference Hörmander9, Theorem 4.5.3]) which says that for
${1}/{q}= \alpha _3({1}/{2}-{1}/{r})$
, we instead use the Hardy–Littlewood–Sobolev inequality (see [Reference Hörmander9, Theorem 4.5.3]) which says that for
![]() $K(t)=|t|^{-1/\gamma }$
and
$K(t)=|t|^{-1/\gamma }$
and
![]() $1<\gamma <\infty $
,
$1<\gamma <\infty $
,
 $$ \begin{align} \|K\ast u\|_{L^{\tilde r}(\mathbb{R})}\lesssim \|u\|_ {L^{p'}(\mathbb{R})} \quad\mbox{for } \frac{1}{\gamma}=\frac{1}{p}+\frac{1}{\tilde r}. \end{align} $$
$$ \begin{align} \|K\ast u\|_{L^{\tilde r}(\mathbb{R})}\lesssim \|u\|_ {L^{p'}(\mathbb{R})} \quad\mbox{for } \frac{1}{\gamma}=\frac{1}{p}+\frac{1}{\tilde r}. \end{align} $$
We apply (3.11) with
![]() $\tilde r=q, p=q$
and
$\tilde r=q, p=q$
and
![]() ${1}/{\gamma }={2}/{q}=2\alpha _3({1}/{2}-{1}/{r})$
to show that
${1}/{\gamma }={2}/{q}=2\alpha _3({1}/{2}-{1}/{r})$
to show that
![]() $t^{-2/q} *: L^{q'}\rightarrow L^{q}$
is bounded for
$t^{-2/q} *: L^{q'}\rightarrow L^{q}$
is bounded for
![]() $q>2$
. Hence, from (3.9),
$q>2$
. Hence, from (3.9),
3.2 Homogeneous Strichartz estimates
We can restate Theorem 2.1 as follows.
Theorem 3.3 (Theorem 2.1).
Let
![]() $(\Omega ,\Delta )$
be defined as before. Let u be a solution of the wave equation on
$(\Omega ,\Delta )$
be defined as before. Let u be a solution of the wave equation on
![]() $\Omega $
:
$\Omega $
:
Then for all T, there exists
![]() $C_T$
such that
$C_T$
such that
with
 $$ \begin{align*} \frac{1}{q}\leq\frac{3}{4}\bigg(\frac{1}{2}-\frac{1}{r}\bigg) \quad\text{and}\quad \beta=3 \bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}. \end{align*} $$
$$ \begin{align*} \frac{1}{q}\leq\frac{3}{4}\bigg(\frac{1}{2}-\frac{1}{r}\bigg) \quad\text{and}\quad \beta=3 \bigg(\frac{1}{2}-\frac{1}{r}\bigg)-\frac{1}{q}. \end{align*} $$
Proof. Using the square function estimates (3.1),
 $$ \begin{align*} \|u\|_{L_t^qL_x^r}\lesssim \bigg(\sum_{j}\|v_j\|_{L_t^qL_x^r}^2\bigg)^{1/2}. \end{align*} $$
$$ \begin{align*} \|u\|_{L_t^qL_x^r}\lesssim \bigg(\sum_{j}\|v_j\|_{L_t^qL_x^r}^2\bigg)^{1/2}. \end{align*} $$
Indeed,
 $$ \begin{align*} \|u\|_{L^r(\Omega)} & \lesssim\bigg\|\bigg(\sum_{j\geq 0}|v_j|^2\bigg)^{1/2}\bigg\|_{L^r(\Omega)}= \bigg\|\sum_{j\geq 0}|v_j|^2\bigg\|_{L^{r/2}(\Omega)}^{1/2} \\ & \lesssim\bigg\{\sum_{j\geq 0}\|v_j^2\|_{L^{r/2}(\Omega)}\bigg\}^{1/2}=\bigg\{\sum_{j\geq 0}\|v_j\|_{L^{r}(\Omega)}^2\bigg\}^{1/2}. \end{align*} $$
$$ \begin{align*} \|u\|_{L^r(\Omega)} & \lesssim\bigg\|\bigg(\sum_{j\geq 0}|v_j|^2\bigg)^{1/2}\bigg\|_{L^r(\Omega)}= \bigg\|\sum_{j\geq 0}|v_j|^2\bigg\|_{L^{r/2}(\Omega)}^{1/2} \\ & \lesssim\bigg\{\sum_{j\geq 0}\|v_j^2\|_{L^{r/2}(\Omega)}\bigg\}^{1/2}=\bigg\{\sum_{j\geq 0}\|v_j\|_{L^{r}(\Omega)}^2\bigg\}^{1/2}. \end{align*} $$
Hence,
 $$ \begin{align*} \|u\|_{L_t^qL_x^r}&\lesssim \bigg\|\bigg\{\sum_{j\geq 0}\|v_j\|_{L_x^{r}}^2\bigg\}^{1/2}\bigg\|_{L_t^q}=\bigg\{\bigg\|\sum_{j\geq 0}\|v_j\|_{L_x^{r}}^2\bigg\|_{L_t^{q/2}}\bigg\}^{1/2},\\ &\lesssim \bigg\{\sum_{j\geq 0}\|\|v_j\|_{L_x^r}^2\|_{L_t^{q/2}}\bigg\}^{1/2}=\bigg\{\sum_{j\geq 0}\|v_j\|_{L_t^qL_x^r}^2\bigg\}^{1/2}. \end{align*} $$
$$ \begin{align*} \|u\|_{L_t^qL_x^r}&\lesssim \bigg\|\bigg\{\sum_{j\geq 0}\|v_j\|_{L_x^{r}}^2\bigg\}^{1/2}\bigg\|_{L_t^q}=\bigg\{\bigg\|\sum_{j\geq 0}\|v_j\|_{L_x^{r}}^2\bigg\|_{L_t^{q/2}}\bigg\}^{1/2},\\ &\lesssim \bigg\{\sum_{j\geq 0}\|\|v_j\|_{L_x^r}^2\|_{L_t^{q/2}}\bigg\}^{1/2}=\bigg\{\sum_{j\geq 0}\|v_j\|_{L_t^qL_x^r}^2\bigg\}^{1/2}. \end{align*} $$
The solution u to the wave equation (3.12) with localised initial data in frequency
![]() $1/h=2^j$
is given by
$1/h=2^j$
is given by
 $$ \begin{align*} u=\sum_j v_j \quad\text{where}\ v_j=\dot{\mathcal U}(t)\chi(2^{-j}D_t)u_0+ \mathcal U(t)\chi(2^{-j}D_t)u_1. \end{align*} $$
$$ \begin{align*} u=\sum_j v_j \quad\text{where}\ v_j=\dot{\mathcal U}(t)\chi(2^{-j}D_t)u_0+ \mathcal U(t)\chi(2^{-j}D_t)u_1. \end{align*} $$
Therefore,
 $$ \begin{align*} \begin{aligned} \|u\|_{L_t^qL_x^r}&\lesssim \bigg( \sum_{j}\|\dot{\mathcal U}(t)\chi(2^{-j}D_t)u_0\|_{L_t^qL_x^r}^2+\|\mathcal U(t)\chi(2^{-j}D_t)u_1\|_{L_t^qL_x^r}^2\bigg)^{1/2},\\ &\lesssim \bigg( \sum_j2^{2j\beta}\|\chi(2^{-j}D_t)u_0\|_ {L^2}^2+2^{2j(\beta-1)}\|\chi(2^{-j}D_t)u_1\|_ {L^2}^2\bigg)^{1/2},\\ &\lesssim \bigg(\sum_j2^{2j\beta}\|\chi(2^{-j}D_t)u_0\|_{L^2}^2\bigg)^{1/2}+\bigg(\sum_j2^{2j(\beta-1)}\|\chi(2^{-j}D_t)u_1\|_{L^2}^2\bigg)^{1/2},\\ &\lesssim \|u_0\|_{\dot{H}^\beta(\Omega)}+\|u_1\|_{\dot{H}^{\beta-1}(\Omega)}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \|u\|_{L_t^qL_x^r}&\lesssim \bigg( \sum_{j}\|\dot{\mathcal U}(t)\chi(2^{-j}D_t)u_0\|_{L_t^qL_x^r}^2+\|\mathcal U(t)\chi(2^{-j}D_t)u_1\|_{L_t^qL_x^r}^2\bigg)^{1/2},\\ &\lesssim \bigg( \sum_j2^{2j\beta}\|\chi(2^{-j}D_t)u_0\|_ {L^2}^2+2^{2j(\beta-1)}\|\chi(2^{-j}D_t)u_1\|_ {L^2}^2\bigg)^{1/2},\\ &\lesssim \bigg(\sum_j2^{2j\beta}\|\chi(2^{-j}D_t)u_0\|_{L^2}^2\bigg)^{1/2}+\bigg(\sum_j2^{2j(\beta-1)}\|\chi(2^{-j}D_t)u_1\|_{L^2}^2\bigg)^{1/2},\\ &\lesssim \|u_0\|_{\dot{H}^\beta(\Omega)}+\|u_1\|_{\dot{H}^{\beta-1}(\Omega)}, \end{aligned} \end{align*} $$
where we used Minkowski’s inequality in the third line.
4 Application
We can use the Strichartz estimates (Theorem 2.1) to obtain the well posedness of the following energy critical nonlinear wave equation in
![]() $(\Omega , \Delta )$
:
$(\Omega , \Delta )$
:
 $$ \begin{align} \begin{aligned} &\quad (\partial_t^2-\Delta)u+u^5=0\quad \text{in } \mathbb{R}_t\times\Omega,\\ &u_{|t=0}=u_0,\quad \partial_t u_{|t=0}=u_1,\quad u_{|x=0}=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\quad (\partial_t^2-\Delta)u+u^5=0\quad \text{in } \mathbb{R}_t\times\Omega,\\ &u_{|t=0}=u_0,\quad \partial_t u_{|t=0}=u_1,\quad u_{|x=0}=0. \end{aligned} \end{align} $$
The solutions to (4.1) satisfy an energy conservation law:
For initial data
![]() $(u_0, u_1)\in H_0^1(\Omega )\times L^2(\Omega )$
, Theorem 2.1 allows the Strichartz triplet
$(u_0, u_1)\in H_0^1(\Omega )\times L^2(\Omega )$
, Theorem 2.1 allows the Strichartz triplet
![]() $q=5, r=10,\,\beta =1$
and we get
$q=5, r=10,\,\beta =1$
and we get
As a consequence, the critical nonlinear wave equation (4.1) is locally well posed in
Moreover, with the arguments in [Reference Burq, Lebeau and Planchon6], we can extend local to global existence for arbitrary (finite energy) data.