Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-14T13:02:35.665Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SECOND MINIMUM/MAXIMUM VALUE OF THE NUMBER OF CYCLIC SUBGROUPS OF FINITE 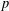$p$-GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  20 April 2020

MIHAI-SILVIU LAZOREC Open the ORCID record for MIHAI-SILVIU LAZOREC [Opens in a new window] ,
RULIN SHEN Open the ORCID record for RULIN SHEN [Opens in a new window]  and
MARIUS TĂRNĂUCEANU Open the ORCID record for MARIUS TĂRNĂUCEANU [Opens in a new window]
MIHAI-SILVIU LAZOREC*
Affiliation:
Faculty of Mathematics, ‘Al.I. Cuza’ University, Iaşi, Romania email mihai.lazorec@student.uaic.ro
RULIN SHEN
Affiliation:
Department of Mathematics, Hubei Minzu University, Enshi, Hubei, PR China email rshen@hbmy.edu.cn
MARIUS TĂRNĂUCEANU
Affiliation:
Faculty of Mathematics, ‘Al.I. Cuza’ University, Iaşi, Romania email tarnauc@uaic.ro
*
✉mihai.lazorec@student.uaic.ro
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 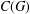$C(G)$ be the poset of cyclic subgroups of a finite group 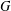$G$ and let 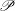$\mathscr{P}$ be the class of 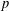$p$-groups of order 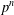$p^{n}$ (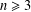$n\geq 3$). Consider the function $\unicode[STIX]{x1D6FC}:\mathscr{P}\longrightarrow (0,1]$ given by 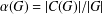$\unicode[STIX]{x1D6FC}(G)=|C(G)|/|G|$. In this paper, we determine the second minimum value of $\unicode[STIX]{x1D6FC}$, as well as the corresponding minimum points. Since the problem of finding the second maximum value of $\unicode[STIX]{x1D6FC}$ has been solved for 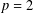$p=2$, we focus on the case of odd primes in determining the second maximum.

Keywords

number of cyclic subgroupsfinite p-groupsexponent of a group

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 20D15: Nilpotent groups, $p$-groups 20D25: Special subgroups (Frattini, Fitting, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 96 - 103
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the European Social Fund, through Operational Programme Human Capital 2014-2020, Project No. POCU/380/6/13/123623. The second author was supported by NSF of China, Grant No. 11561021.

References

Aivazidis, S. and Müller, T., ‘Finite non-cyclic p-groups whose number of subgroups is minimal’, Arch. Math. (Basel) 114(1) (2020), 13–17.10.1007/s00013-019-01376-9CrossRefGoogle Scholar
Berkovich, Y., Groups of Prime Power Order, Vol. 1 (de Gruyter, Berlin, 2008).10.1515/9783110208221CrossRefGoogle Scholar
Burnside, W., Theory of Groups of Finite Order, 2nd edn (Dover Publications, Inc., New York, 1955).Google Scholar
Butler, L. M., ‘Subgroup lattices and symmetric functions’, Mem. Amer. Math. Soc. 112 (1994), 1–160.Google Scholar
Garonzi, M. and Lima, I., ‘On the number of cyclic subgroups of a finite group’, Bull. Braz. Math. Soc. 49 (2018), 515–530.10.1007/s00574-018-0068-xCrossRefGoogle Scholar
Jafari, M. H. and Madadi, A. R., ‘On the number of cyclic subgroups of a finite group’, Bull. Korean Math. Soc. 54(60) (2017), 2141–2147.Google Scholar
Laffey, T. J., ‘The number of solutions of x 3 = 1 in a 3-group’, Math. Z. 149(2) (1976), 43–45.10.1007/BF01301629CrossRefGoogle Scholar
Lazorec, M. S., ‘A connection between the number of subgroups and the order of a finite group’, Preprint, 2019, arXiv:1901.06425.10.1142/S0219498822500013CrossRefGoogle Scholar
Lazorec, M. S. and Tărnăuceanu, M., ‘A note on the number of cyclic subgroups of a finite group’, Bull. Math. Soc. Sci. Math. Roumanie 62/110(4) (2019), 403–416.Google Scholar
Miller, G. A., ‘An extension of Sylow’s theorem’, Proc. Lond. Math. Soc. Ser. 2 2 (1905), 142–143.10.1112/plms/s2-2.1.142CrossRefGoogle Scholar
Miller, G. A., ‘The groups of order p m which contain exactly p cyclic subgroups of order p a’, Trans. Amer. Math. Soc. 7(2) (1906), 228–232.Google Scholar
Qu, H., ‘Finite non-elementary abelian p-groups whose number of subgroups is maximal’, Israel J. Math. 195 (2013), 773–781.10.1007/s11856-012-0114-0CrossRefGoogle Scholar
Richards, I. M., ‘A remark on the number of cyclic subgroups of a finite group’, Amer. Math. Monthly 91(9) (1984), 571–572.10.1080/00029890.1984.11971498CrossRefGoogle Scholar
Sædén Ståhl, G., Laine, J. and Behm, G., On $p$-groups of Low Power Order, Bachelor Thesis, KTH Royal Institute of Technology, 2010.Google Scholar
Suzuki, M., Group Theory, Vols. I, II (Springer, Berlin, 1982, 1986).Google Scholar
Tărnăuceanu, M., ‘On a conjecture by Haipeng Qu’, J. Group Theory 22(3) (2019), 505–514.10.1515/jgth-2018-0202CrossRefGoogle Scholar
Tărnăuceanu, M. and Tóth, L., ‘Cyclicity degrees of finite groups’, Acta Math. Hungar. 145 (2015), 489–504.10.1007/s10474-015-0480-2CrossRefGoogle Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.9.3, 2018, https://www.gap-system.org.Google Scholar