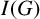1 Introduction
Let
![]() $S=\mathsf {k}[x_{1},\ldots ,x_{n}]$
be a polynomial ring, where
$S=\mathsf {k}[x_{1},\ldots ,x_{n}]$
be a polynomial ring, where
![]() $\mathsf {k}$
is a field. For a homogeneous ideal I, Cutkosky et al. [Reference Cutkosky, Herzog and Trung5] and independently Kodiyalam [Reference Kodiyalam11] proved that
$\mathsf {k}$
is a field. For a homogeneous ideal I, Cutkosky et al. [Reference Cutkosky, Herzog and Trung5] and independently Kodiyalam [Reference Kodiyalam11] proved that
![]() $\mathrm {reg}(S/I^{s})=as+b$
for some
$\mathrm {reg}(S/I^{s})=as+b$
for some
![]() $a, b \in \mathbb {Z}$
and
$a, b \in \mathbb {Z}$
and
![]() $s\gg 0.$
The value of a can be determined by the degrees of generators of I but the value of b is quite mysterious. During the last few decades, many researchers have studied the problem of understanding the value of b for some special classes of ideals, for example, edge ideals and cover ideals. In this paper, we consider the edge ideal
$s\gg 0.$
The value of a can be determined by the degrees of generators of I but the value of b is quite mysterious. During the last few decades, many researchers have studied the problem of understanding the value of b for some special classes of ideals, for example, edge ideals and cover ideals. In this paper, we consider the edge ideal
![]() $I(G)$
of a bipartite graph G and find an upper bound for the value of b in terms of a combinatorial invariant of G.
$I(G)$
of a bipartite graph G and find an upper bound for the value of b in terms of a combinatorial invariant of G.
For any graph G, it is known that
where
![]() $\nu (G)$
denotes the induced matching number of G and co-chord
$\nu (G)$
denotes the induced matching number of G and co-chord
![]() $(G)$
denotes the co-chordal number of G (see [Reference Katzman10, Reference Woodroofe14]). Bıyıkoğlu and Civan in [Reference Bıyıkoğlu and Civan4] proved that for any graph G,
$(G)$
denotes the co-chordal number of G (see [Reference Katzman10, Reference Woodroofe14]). Bıyıkoğlu and Civan in [Reference Bıyıkoğlu and Civan4] proved that for any graph G,
![]() $\mathrm {reg}(S/I(G) ) \leq \beta (G),$
where
$\mathrm {reg}(S/I(G) ) \leq \beta (G),$
where
![]() $\beta (G)$
is called the upper independent vertex-wise domination set of G (see Definition 2.1(vi)). Beyarslan et al. in [Reference Beyarslan, Hà and Trung3] proved that for any graph G,
$\beta (G)$
is called the upper independent vertex-wise domination set of G (see Definition 2.1(vi)). Beyarslan et al. in [Reference Beyarslan, Hà and Trung3] proved that for any graph G,
Moreover, they proved that in the special cases of forests (for
![]() $s \geq 1$
) and cycles (
$s \geq 1$
) and cycles (
![]() $s \geq 2$
), the equality holds. In [Reference Jayanthan, Narayanan and Selvaraja8], it is shown that for bipartite graphs,
$s \geq 2$
), the equality holds. In [Reference Jayanthan, Narayanan and Selvaraja8], it is shown that for bipartite graphs,
Recently, Herzog and Hibi [Reference Herzog and Hibi7] obtained a new upper bound for the regularity of powers of the ideal of a graph G. They proved that
where c is the dimension of the independence complex
![]() $\Delta (G)$
of G.
$\Delta (G)$
of G.
In Section 3, we prove the main result of this paper, which gives a new upper bound for
![]() $\mathrm {reg}(S/I(G)^{s} )$
for any bipartite graph G.
$\mathrm {reg}(S/I(G)^{s} )$
for any bipartite graph G.
Theorem 1.1 (Theorem 3.11).
Let G be a bipartite graph and
![]() $I(G)$
be its edge ideal. Then
$I(G)$
be its edge ideal. Then
![]() $\mathrm {reg}(S/I(G)^{s+1}) \leq 2s+\beta (G)$
for all
$\mathrm {reg}(S/I(G)^{s+1}) \leq 2s+\beta (G)$
for all
![]() $s \geq 0$
.
$s \geq 0$
.
To prove Theorem 3.11, we use the technique of even-connection with respect to the s-fold product
![]() $e_{1} \cdots e_{s}$
of edges (see Definition 2.5), which was introduced by Banerjee in [Reference Banerjee2]. Alilooee and Banerjee [Reference Alilooee and Banerjee1] proved that if G is a bipartite graph, then the colon ideal
$e_{1} \cdots e_{s}$
of edges (see Definition 2.5), which was introduced by Banerjee in [Reference Banerjee2]. Alilooee and Banerjee [Reference Alilooee and Banerjee1] proved that if G is a bipartite graph, then the colon ideal
![]() $I(G)^{s+1}:e_{1} \cdots e_{s}$
is a quadratic square-free monomial ideal. Further, the graph
$I(G)^{s+1}:e_{1} \cdots e_{s}$
is a quadratic square-free monomial ideal. Further, the graph
![]() $G^{\prime }$
associated to
$G^{\prime }$
associated to
![]() $I(G)^{s+1}:e_{1} \cdots e_{s}$
is also a bipartite graph on the same partition and
$I(G)^{s+1}:e_{1} \cdots e_{s}$
is also a bipartite graph on the same partition and
![]() $G^{\prime }$
is the union of G with all the even-connections with respect to the s-fold product
$G^{\prime }$
is the union of G with all the even-connections with respect to the s-fold product
![]() $e_{1} \cdots e_{s}$
(see Remark 3.9).
$e_{1} \cdots e_{s}$
(see Remark 3.9).
In Section 4, we study the regularity of powers of edge ideals of the bipartite Kneser graph
![]() $\mathcal {H}(m,k)$
for
$\mathcal {H}(m,k)$
for
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $m \geq 2k$
(see Definition 2.2). Bipartite Kneser graphs are of great interest because they are Hamiltonian, as shown by Mütze and Su [Reference Mütze and Su13]. We are interested in finding the regularity of powers of edge ideals of bipartite Kneser graphs. In [Reference Kumar, Singh and Verma12], it is shown that
$m \geq 2k$
(see Definition 2.2). Bipartite Kneser graphs are of great interest because they are Hamiltonian, as shown by Mütze and Su [Reference Mütze and Su13]. We are interested in finding the regularity of powers of edge ideals of bipartite Kneser graphs. In [Reference Kumar, Singh and Verma12], it is shown that
 $$ \begin{align*}2(s-1)+{2k\choose k}\leq \mathrm{reg}(S/{I(\mathcal{H}(m,k))}^{s})\leq 2(s-1)+{m\choose k},\end{align*} $$
$$ \begin{align*}2(s-1)+{2k\choose k}\leq \mathrm{reg}(S/{I(\mathcal{H}(m,k))}^{s})\leq 2(s-1)+{m\choose k},\end{align*} $$
and the lower bound is attained if
![]() $m=2k+1$
. It is known that the problem of finding the induced matching number of the graph is an NP-hard problem. Given
$m=2k+1$
. It is known that the problem of finding the induced matching number of the graph is an NP-hard problem. Given
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $m \geq 2k+1$
, we compute the induced matching number of the bipartite Kneser graph
$m \geq 2k+1$
, we compute the induced matching number of the bipartite Kneser graph
![]() $\mathcal {H}(m,k)$
.
$\mathcal {H}(m,k)$
.
Theorem 1.2 (Corollary 4.3).
For
![]() $m\geq 2k+1$
, let
$m\geq 2k+1$
, let
![]() $G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then the induced matching number of G is given by
$G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then the induced matching number of G is given by
![]() $\nu (G) = \binom {2k}{k}.$
$\nu (G) = \binom {2k}{k}.$
The following question is posed in [Reference Beyarslan, Hà and Trung3]: for which graphs G does
For certain classes of graphs, for example, the bipartite
![]() $P_{6}$
-free graph and very well-covered, unmixed bipartite, weakly chordal bipartite, forest graphs, it is known that
$P_{6}$
-free graph and very well-covered, unmixed bipartite, weakly chordal bipartite, forest graphs, it is known that
![]() $\textrm {reg}(S/I(G)^{s})=2s+\nu (G)-2$
for
$\textrm {reg}(S/I(G)^{s})=2s+\nu (G)-2$
for
![]() $s \gg 0$
(see [Reference Beyarslan, Hà and Trung3, Reference Jayanthan, Narayanan and Selvaraja8, Reference Jayanthan and Selvaraja9]). Using Theorem 3.11, we prove that the regularity of powers of edge ideals of
$s \gg 0$
(see [Reference Beyarslan, Hà and Trung3, Reference Jayanthan, Narayanan and Selvaraja8, Reference Jayanthan and Selvaraja9]). Using Theorem 3.11, we prove that the regularity of powers of edge ideals of
![]() $\mathcal {H}(m,k)$
attains the lower bound.
$\mathcal {H}(m,k)$
attains the lower bound.
Theorem 1.3 (Corollary 4.4).
For
![]() $m\geq 2k+1$
, let
$m\geq 2k+1$
, let
![]() $G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then, for all
$G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then, for all
![]() $s>0$
,
$s>0$
,
![]() $ \mathrm {reg}(S/I(G)^{s} )=2(s-1)+\binom {2k}{k}.$
$ \mathrm {reg}(S/I(G)^{s} )=2(s-1)+\binom {2k}{k}.$
2 Preliminaries
For a positive integer
![]() $n,$
we write
$n,$
we write
![]() $[n]=\{1, 2,\ldots , n\}.$
For a finite set Y, the family of all subsets of Y of size s is denoted by
$[n]=\{1, 2,\ldots , n\}.$
For a finite set Y, the family of all subsets of Y of size s is denoted by
![]() $Y^{(s)}$
.
$Y^{(s)}$
.
Definition 2.1. Let G be a simple graph with vertex set
![]() $V(G)=\{x_{1},\ldots , x_{n}\}$
and edge set
$V(G)=\{x_{1},\ldots , x_{n}\}$
and edge set
![]() $E(G)$
.
$E(G)$
.
-
(i) For a pair of vertices
 $x_{i},x_{j}\in V(G)$
, we say
$x_{i},x_{j}\in V(G)$
, we say
 $x_{i}$
is adjacent to
$x_{i}$
is adjacent to
 $x_{j}$
if and only if
$x_{j}$
if and only if
 $x_{i}x_{j}\in E(G).$
$x_{i}x_{j}\in E(G).$
-
(ii) A subset W of V is called an independent set if none of the edges of G has both endpoints in W.
-
(iii) For a vertex
 $v\in V$
, the open neighbourhood of v is
$v\in V$
, the open neighbourhood of v is
 $N_{G}(v)=\{x: xv\in E(G)\}$
and the closed neighbourhood of v is
$N_{G}(v)=\{x: xv\in E(G)\}$
and the closed neighbourhood of v is
 $N_{G}[v]=N_{G}(v)\cup \{v\}$
.
$N_{G}[v]=N_{G}(v)\cup \{v\}$
. -
(iv) For an edge
 $e=x_{i}x_{j}$
, we define
$e=x_{i}x_{j}$
, we define
 $N_{G}[e]=N_{G}[x_{i}]\cup N_{G}[x_{j}].$
$N_{G}[e]=N_{G}[x_{i}]\cup N_{G}[x_{j}].$
-
(v) An independent set W is called a vertex dominant set if
 $N_{G}[e]\cap W\neq \varnothing $
for any edge e in G. It is called a minimal vertex dominant set if any proper subset of W is not a vertex-wise dominant set of G.
$N_{G}[e]\cap W\neq \varnothing $
for any edge e in G. It is called a minimal vertex dominant set if any proper subset of W is not a vertex-wise dominant set of G. -
(vi) The upper independent vertex-wise domination number of a graph G is defined by
 $\beta (G)=\max \{|W|: W\text { is an independent minimal vertex dominating set of } G\}.$
$\beta (G)=\max \{|W|: W\text { is an independent minimal vertex dominating set of } G\}.$
-
(vii) A graph G is called bipartite if
 $V(G)=X \sqcup Y$
for two independent subsets X and Y of
$V(G)=X \sqcup Y$
for two independent subsets X and Y of
 $V(G)$
.
$V(G)$
. -
(viii) A subgraph
 $G^{\prime }$
of G is called induced if for every pair of vertices
$G^{\prime }$
of G is called induced if for every pair of vertices
 $x_{i}, x_{j}\in V(G^{\prime })$
,
$x_{i}, x_{j}\in V(G^{\prime })$
,
 $x_{i}x_{j}\in E(G^{\prime })$
if and only if
$x_{i}x_{j}\in E(G^{\prime })$
if and only if
 $x_{i}x_{j}\in E(G)$
.
$x_{i}x_{j}\in E(G)$
. -
(ix) A matching of G is a subgraph of G consisting of pairwise disjoint edges. If the subgraph is an induced subgraph, then the matching is called an induced matching. The largest size of an induced matching in G is called the induced matching number, denoted by
 $\nu (G).$
$\nu (G).$
-
(x) The graph G is a cycle of length n if after relabelling the vertices of G, the edge set is
 $E(G)=\{x_{1}x_{2},\ldots , x_{n-1}x_{n},x_{n}x_{1}\}$
.
$E(G)=\{x_{1}x_{2},\ldots , x_{n-1}x_{n},x_{n}x_{1}\}$
. -
(xi) A finite sequence of vertices
 $x_{i_{1}},\ldots , x_{i_{r}}$
is called a path from
$x_{i_{1}},\ldots , x_{i_{r}}$
is called a path from
 $x_{i_{1}}$
to
$x_{i_{1}}$
to
 $x_{i_{r}}$
in G if
$x_{i_{r}}$
in G if
 $x_{i_{j}}x_{i_{j+1}}\in E(G)$
for
$x_{i_{j}}x_{i_{j+1}}\in E(G)$
for
 $1\leq j\leq r-1$
.
$1\leq j\leq r-1$
. -
(xii) A graph is called co-chordal if its complement graph
 $G^{c}$
does not have any induced cycle of length greater than or equal to
$G^{c}$
does not have any induced cycle of length greater than or equal to
 $4$
. The co-chordal number, denoted by co-chord
$4$
. The co-chordal number, denoted by co-chord
 $(G)$
, is the minimum number of co-chordal subgraphs required to cover the edges of
$(G)$
, is the minimum number of co-chordal subgraphs required to cover the edges of
 $G.$
$G.$
Definition 2.2. The bipartite Kneser graph
![]() $\mathcal {H}(m,k)$
is a graph with vertex set
$\mathcal {H}(m,k)$
is a graph with vertex set
![]() $V(G)=[m]^{(k)} \cup [m]^{(m-k)}$
and two distinct vertices
$V(G)=[m]^{(k)} \cup [m]^{(m-k)}$
and two distinct vertices
![]() $A, B$
are adjacent if and only if
$A, B$
are adjacent if and only if
![]() $A\subset B$
or
$A\subset B$
or
![]() $B\subset A. $
For
$B\subset A. $
For
![]() $m= 2k$
,
$m= 2k$
,
![]() $\mathcal {H}(m,k)$
does not have any edges, so we assume that
$\mathcal {H}(m,k)$
does not have any edges, so we assume that
![]() $m \geq 2k +1.$
$m \geq 2k +1.$
Definition 2.3. Let
![]() $\mathsf {k}$
be a field and
$\mathsf {k}$
be a field and
![]() $S=\mathsf {k}[x_{1},x_{2},\ldots ,x_{n}]$
be a standard graded polynomial ring over
$S=\mathsf {k}[x_{1},x_{2},\ldots ,x_{n}]$
be a standard graded polynomial ring over
![]() $\mathsf {k}$
. The Castelnuovo–Mumford regularity of a finitely generated graded S-Module M is given by
$\mathsf {k}$
. The Castelnuovo–Mumford regularity of a finitely generated graded S-Module M is given by
![]() $\mathrm {reg}(M)=\max _{i,j}\{\kern1.3pt j-i:\mathrm {Tor}_{i}{(M,\mathsf {k})}_{j} \neq 0\}.$
$\mathrm {reg}(M)=\max _{i,j}\{\kern1.3pt j-i:\mathrm {Tor}_{i}{(M,\mathsf {k})}_{j} \neq 0\}.$
Definition 2.4. Let G be a simple graph with the vertex set
![]() $\{x_{1},\ldots ,x_{k}\}$
(without isolated vertices). Then the edge ideal of G is defined as
$\{x_{1},\ldots ,x_{k}\}$
(without isolated vertices). Then the edge ideal of G is defined as
Definition 2.5 [Reference Banerjee2, Definition 6.2].
Let G be a graph on the vertex set V. Then vertices
![]() $x, y\in V$
are called even-connected with respect to the s-fold product
$x, y\in V$
are called even-connected with respect to the s-fold product
![]() $e_{1}\cdots e_{s}$
of edges in G if there exists a path
$e_{1}\cdots e_{s}$
of edges in G if there exists a path
![]() $p_{0}p_{1}\ldots p_{2k+1}$
in G such that:
$p_{0}p_{1}\ldots p_{2k+1}$
in G such that:
-
(a)
 $p_{0}=x$
and
$p_{0}=x$
and
 $p_{2k+1}=y$
;
$p_{2k+1}=y$
; -
(b)
 $p_{2l+1}p_{2l+2}=e_{i}$
for some i for all l with
$p_{2l+1}p_{2l+2}=e_{i}$
for some i for all l with
 $0\leq l \leq k-1$
;
$0\leq l \leq k-1$
; -
(c)
 $|\{l\geq 0 \mid p_{2l+1}p_{2l+2}=e_{i}\}|\leq |\{\kern1.3pt j \mid e_{j}=e_{i}\}|$
for all i.
$|\{l\geq 0 \mid p_{2l+1}p_{2l+2}=e_{i}\}|\leq |\{\kern1.3pt j \mid e_{j}=e_{i}\}|$
for all i.
Theorem 2.6 [Reference Banerjee2, Theorem 5.2].
Let G be a simple graph and the set of minimal monomial generators of
![]() $I(G)^{s}$
be
$I(G)^{s}$
be
![]() $\{m_{1},\ldots ,m_{k}\}$
, where
$\{m_{1},\ldots ,m_{k}\}$
, where
![]() $s>0$
. Then,
$s>0$
. Then,
3 Vertex-wise domination number
In general, there is no relation between
![]() $\beta (G)$
and co-chord
$\beta (G)$
and co-chord
![]() $(G)$
, for a simple graph G. For example, if
$(G)$
, for a simple graph G. For example, if
![]() $P_{4}$
is a simple path on
$P_{4}$
is a simple path on
![]() $4$
vertices, one can check that
$4$
vertices, one can check that
![]() $\beta (P_{4})=2$
, but
$\beta (P_{4})=2$
, but
![]() $P_{4}$
is a co-chordal graph. However, in [Reference Bıyıkoğlu and Civan4], it is shown that
$P_{4}$
is a co-chordal graph. However, in [Reference Bıyıkoğlu and Civan4], it is shown that
![]() $\beta (C_{7})=2$
and co-chord
$\beta (C_{7})=2$
and co-chord
![]() $(C_{7})=3$
, where
$(C_{7})=3$
, where
![]() $C_{7}$
denotes the cycle of length
$C_{7}$
denotes the cycle of length
![]() $7$
.
$7$
.
Remark 3.1. Let W be a minimal vertex dominant set of G and
![]() $w\in W$
. Then there exists an edge
$w\in W$
. Then there exists an edge
![]() $e\in G$
such that
$e\in G$
such that
![]() $N_{G}[e]\cap W=\{w\}$
.
$N_{G}[e]\cap W=\{w\}$
.
Notation 3.2. Let G be a triangle-free graph and
![]() $I(G)$
its edge ideal. For
$I(G)$
its edge ideal. For
![]() $x_{1}x_{2} \in E(G)$
, let
$x_{1}x_{2} \in E(G)$
, let
![]() $G^{\prime }$
be the graph associated to the monomial ideal
$G^{\prime }$
be the graph associated to the monomial ideal
![]() $I(G)^{2}:x_{1}x_{2}$
. Denote by
$I(G)^{2}:x_{1}x_{2}$
. Denote by
![]() ${N_{G}(x_{1})\setminus \{x_{2}\}=\{x_{1,1},\ldots , x_{1,r}\}=X_{1}}$
and
${N_{G}(x_{1})\setminus \{x_{2}\}=\{x_{1,1},\ldots , x_{1,r}\}=X_{1}}$
and
![]() $N_{G}(x_{2})\setminus \{x_{1}\}=\{x_{2,1},\ldots , x_{2,s}\}=X_{2}.$
To illustrate the notation, we consider a graph G on the vertex set
$N_{G}(x_{2})\setminus \{x_{1}\}=\{x_{2,1},\ldots , x_{2,s}\}=X_{2}.$
To illustrate the notation, we consider a graph G on the vertex set
![]() $\{x_{1},x_{2},x_{3},x_{1,1},x_{1,2},x_{2,1},x_{2,2}\}$
and the edge set
$\{x_{1},x_{2},x_{3},x_{1,1},x_{1,2},x_{2,1},x_{2,2}\}$
and the edge set
![]() $E(G)=\{x_{1}x_{2},x_{1}x_{1,1},x_{1}x_{1,2},x_{2}x_{2,1},x_{2}x_{2,2},x_{1,1}x_{3}\}$
, as shown in Figure 1. Then
$E(G)=\{x_{1}x_{2},x_{1}x_{1,1},x_{1}x_{1,2},x_{2}x_{2,1},x_{2}x_{2,2},x_{1,1}x_{3}\}$
, as shown in Figure 1. Then
![]() $I(G)^{2}:x_{1}x_{2}=I(G)+\langle x_{1,1}x_{2,1},x_{1,1}x_{2,2},x_{1,2}x_{2,1},x_{1,2}x_{2,2}\rangle $
, that is,
$I(G)^{2}:x_{1}x_{2}=I(G)+\langle x_{1,1}x_{2,1},x_{1,1}x_{2,2},x_{1,2}x_{2,1},x_{1,2}x_{2,2}\rangle $
, that is,
![]() $G^{\prime }$
is obtained from the graph G by connecting all vertices of
$G^{\prime }$
is obtained from the graph G by connecting all vertices of
![]() $X_{1}$
with vertices of
$X_{1}$
with vertices of
![]() $X_{2}$
.
$X_{2}$
.

Figure 1 Illustrative example for Notation 3.2.
Proposition 3.3. Let G be a triangle-free graph and
![]() $I(G)$
be its edge ideal. Let
$I(G)$
be its edge ideal. Let
![]() $e \in E(G)$
and
$e \in E(G)$
and
![]() $G^{\prime }$
be the graph associated to the monomial ideal
$G^{\prime }$
be the graph associated to the monomial ideal
![]() $I(G)^{2}:e$
. Then
$I(G)^{2}:e$
. Then
![]() $\beta (G^{\prime })\leq \beta (G)$
.
$\beta (G^{\prime })\leq \beta (G)$
.
We prove this proposition in the following sequence of lemmas.
Lemma 3.4. With notation as in Notation 3.2, let W be a minimal vertex dominant set in
![]() $G^{\prime }$
such that
$G^{\prime }$
such that
![]() $W\cap (X_{1}\cup X_{2})=\varnothing $
. Then W is a minimal vertex dominant set in G.
$W\cap (X_{1}\cup X_{2})=\varnothing $
. Then W is a minimal vertex dominant set in G.
Proof. Since
![]() $N_{G}[e]\subset N_{G^{\prime }}[e]\subset N_{G}[e]\cup X_{1}\cup X_{2}$
for any
$N_{G}[e]\subset N_{G^{\prime }}[e]\subset N_{G}[e]\cup X_{1}\cup X_{2}$
for any
![]() $e\in E(G)$
, we have
$e\in E(G)$
, we have
![]() $N_{G}[e]\cap W=N_{G^{\prime }}[e]\cap W$
. Hence, W is a vertex dominant set in G. We claim that W is a minimal vertex dominant set in G. In contrast, assume that W is not a minimal vertex dominant set in G. Then there exists a vertex
$N_{G}[e]\cap W=N_{G^{\prime }}[e]\cap W$
. Hence, W is a vertex dominant set in G. We claim that W is a minimal vertex dominant set in G. In contrast, assume that W is not a minimal vertex dominant set in G. Then there exists a vertex
![]() $v\in W$
such that
$v\in W$
such that
![]() $W_{1}=W\setminus \{v\}$
is a vertex dominant set in G. Since W is a minimal vertex dominant set in
$W_{1}=W\setminus \{v\}$
is a vertex dominant set in G. Since W is a minimal vertex dominant set in
![]() $G^{\prime }$
,
$G^{\prime }$
,
![]() $W_{1}$
is not a vertex dominant set in
$W_{1}$
is not a vertex dominant set in
![]() $G^{\prime }$
. There exists an edge
$G^{\prime }$
. There exists an edge
![]() $f\in E(G^{\prime })$
such that
$f\in E(G^{\prime })$
such that
![]() $W_{1}\cap N_{G^{\prime }}[f]=\varnothing $
. However,
$W_{1}\cap N_{G^{\prime }}[f]=\varnothing $
. However,
![]() $N_{G}[f]\cap W_{1} = N_{G^{\prime }}[f] \cap W_{1} = \varnothing $
, so
$N_{G}[f]\cap W_{1} = N_{G^{\prime }}[f] \cap W_{1} = \varnothing $
, so
![]() $f\notin E(G)$
and hence
$f\notin E(G)$
and hence
![]() $f=x_{1,i}x_{2,j}$
for some
$f=x_{1,i}x_{2,j}$
for some
![]() $i, j$
.
$i, j$
.
However, note that
![]() $v\in N_{G^{\prime }}[f]$
. Since
$v\in N_{G^{\prime }}[f]$
. Since
![]() $v\notin X_{1}\cup X_{2}$
, then
$v\notin X_{1}\cup X_{2}$
, then
![]() $v\notin \{x_{1,i},x_{2,j}\}$
and
$v\notin \{x_{1,i},x_{2,j}\}$
and
![]() $v\in N_{G}[f].$
Without loss of generality, assume that
$v\in N_{G}[f].$
Without loss of generality, assume that
![]() $vx_{1,i}\in E(G)$
. Since
$vx_{1,i}\in E(G)$
. Since
![]() $N_{G}[f]\cap W_{1}=\varnothing $
, we have
$N_{G}[f]\cap W_{1}=\varnothing $
, we have
![]() $N_{G}[x_{1,i}]\cap W_{1}=\varnothing $
and so
$N_{G}[x_{1,i}]\cap W_{1}=\varnothing $
and so
![]() $N_{G}[v]\cap W_{1}\neq \varnothing $
. This implies that v and some of its adjacent vertices are in W, contradicting the hypothesis that W is an independent set.
$N_{G}[v]\cap W_{1}\neq \varnothing $
. This implies that v and some of its adjacent vertices are in W, contradicting the hypothesis that W is an independent set.
Lemma 3.5. With notation as in Notation 3.2, let W be a minimal vertex dominant set in
![]() $G^{\prime }$
such that
$G^{\prime }$
such that
![]() $W\cap X_{1}\neq \varnothing $
. Then
$W\cap X_{1}\neq \varnothing $
. Then
![]() $W\cup \{x_{2}\}$
is a vertex dominant set in G.
$W\cup \{x_{2}\}$
is a vertex dominant set in G.
Proof. First of all, note that since W is an independent set in
![]() $G^{\prime }$
and
$G^{\prime }$
and
![]() $W\cap X_{1}\neq \varnothing $
, we get
$W\cap X_{1}\neq \varnothing $
, we get
![]() $W\cap X_{2}=\varnothing $
. Let f be an edge in G. If
$W\cap X_{2}=\varnothing $
. Let f be an edge in G. If
![]() $x_{2}\in N_{G}[f]$
, then we are through. Suppose
$x_{2}\in N_{G}[f]$
, then we are through. Suppose
![]() $x_{2}\notin N_{G}[f]$
. This implies that
$x_{2}\notin N_{G}[f]$
. This implies that
![]() $x_{2,j}$
is not an endpoint of the edge f for any j. Hence,
$x_{2,j}$
is not an endpoint of the edge f for any j. Hence,
![]() $N_{G}[f]\subset N_{G^{\prime }}[f]\subset N_{G}[f]\cup X_{2}.$
Since
$N_{G}[f]\subset N_{G^{\prime }}[f]\subset N_{G}[f]\cup X_{2}.$
Since
![]() $W \cap X_{2}=\varnothing $
, we get
$W \cap X_{2}=\varnothing $
, we get
![]() $N_{G}[f]\cap W=N_{G^{\prime }}[f]\cap W\neq \varnothing $
, which proves the lemma.
$N_{G}[f]\cap W=N_{G^{\prime }}[f]\cap W\neq \varnothing $
, which proves the lemma.
Lemma 3.6. With notation as in Notation 3.2, let W be a minimal vertex dominant set in
![]() $G^{\prime }$
such that
$G^{\prime }$
such that
![]() $W\cap X_{1}\neq \varnothing $
. Let
$W\cap X_{1}\neq \varnothing $
. Let
![]() $W_{1}=W\cup \{x_{2}\}.$
Suppose
$W_{1}=W\cup \{x_{2}\}.$
Suppose
![]() $W_{1}\setminus \{v\}$
is a vertex dominant set in G for some
$W_{1}\setminus \{v\}$
is a vertex dominant set in G for some
![]() $v\in W_{1}$
. Then
$v\in W_{1}$
. Then
![]() $v\in X_{1}\cup \{x_{2}\}$
.
$v\in X_{1}\cup \{x_{2}\}$
.
Proof. On the contrary, assume that
![]() $v\notin X_{1}\cup \{x_{2}\}$
. Since
$v\notin X_{1}\cup \{x_{2}\}$
. Since
![]() $W\setminus \{v\}$
is not a vertex dominant set in
$W\setminus \{v\}$
is not a vertex dominant set in
![]() $G^{\prime }$
, there is an edge
$G^{\prime }$
, there is an edge
![]() $f\in E(G^{\prime })$
such that
$f\in E(G^{\prime })$
such that
![]() $N_{G^{\prime }}[f]\cap ( W\setminus \{v\} )=\varnothing $
. If
$N_{G^{\prime }}[f]\cap ( W\setminus \{v\} )=\varnothing $
. If
![]() $f= x_{1,i}x_{2,j}$
for some
$f= x_{1,i}x_{2,j}$
for some
![]() $i, j$
, then
$i, j$
, then
![]() $X_{1}\subset N_{G^{\prime }}[f]$
. Hence,
$X_{1}\subset N_{G^{\prime }}[f]$
. Hence,
![]() $X_{1} \cap ( W\setminus \{v\} ) \subset N_{G^{\prime }}[f]\cap ( W\setminus \{v\} )\neq \varnothing ,$
which is a contradiction to our hypothesis. Therefore,
$X_{1} \cap ( W\setminus \{v\} ) \subset N_{G^{\prime }}[f]\cap ( W\setminus \{v\} )\neq \varnothing ,$
which is a contradiction to our hypothesis. Therefore,
![]() $f\in E(G)$
. Since
$f\in E(G)$
. Since
![]() $N_{G}[f]\subset N_{G^{\prime }}[f]$
and
$N_{G}[f]\subset N_{G^{\prime }}[f]$
and
![]() $N_{G^{\prime }}[f]\cap W\setminus \{v\}=\varnothing $
,
$N_{G^{\prime }}[f]\cap W\setminus \{v\}=\varnothing $
,
![]() $N_{G}[f]\cap W\setminus \{v\}=\varnothing $
. Also, we have
$N_{G}[f]\cap W\setminus \{v\}=\varnothing $
. Also, we have
![]() $N_{G}[f] \cap W_{1} \setminus \{v\} = N_{G}[f] \cap (W \cup \{x_{2}\}) \setminus \{v\} \neq \varnothing .$
Because,
$N_{G}[f] \cap W_{1} \setminus \{v\} = N_{G}[f] \cap (W \cup \{x_{2}\}) \setminus \{v\} \neq \varnothing .$
Because,
![]() $v \neq x_{2},$
we get
$v \neq x_{2},$
we get
![]() $ x_{2} \in N_{G}[f]$
. Since
$ x_{2} \in N_{G}[f]$
. Since
![]() $W_{1}\setminus \{v\}$
is a vertex dominant set in
$W_{1}\setminus \{v\}$
is a vertex dominant set in
![]() $G,$
we get
$G,$
we get
![]() $X_{1}\subset N_{G^{\prime }}[f]$
, reaching the same contradiction.
$X_{1}\subset N_{G^{\prime }}[f]$
, reaching the same contradiction.
Lemma 3.7. With notation as in Notation 3.2, let W be a minimal vertex dominant set in
![]() $G^{\prime }$
with
$G^{\prime }$
with
![]() $W\cap X_{1}\neq \varnothing $
. Let
$W\cap X_{1}\neq \varnothing $
. Let
![]() $v\in W\cap X_{1}$
. Then
$v\in W\cap X_{1}$
. Then
![]() $\widehat {W}=W\setminus \{v\}$
is not a vertex dominant set in G.
$\widehat {W}=W\setminus \{v\}$
is not a vertex dominant set in G.
Proof. On the contrary, assume that
![]() $\widehat {W}=W \setminus \{v\}$
is a vertex dominant set in G. Since
$\widehat {W}=W \setminus \{v\}$
is a vertex dominant set in G. Since
![]() $\widehat {W}$
is not a vertex dominant set in
$\widehat {W}$
is not a vertex dominant set in
![]() $G^{\prime }$
, there exists
$G^{\prime }$
, there exists
![]() $f\in E(G^{\prime })$
such that
$f\in E(G^{\prime })$
such that
![]() $N_{G^{\prime }}[f]\cap \widehat {W}=\varnothing $
. This implies that
$N_{G^{\prime }}[f]\cap \widehat {W}=\varnothing $
. This implies that
![]() $v\in N_{G^{\prime }}[f]$
. Note that
$v\in N_{G^{\prime }}[f]$
. Note that
![]() $f\notin E(G).$
As for
$f\notin E(G).$
As for
![]() $f\in E(G)$
, we have
$f\in E(G)$
, we have
![]() $N_{G}[f]\cap \widehat {W}\subset N_{G^{\prime }}[f]\cap \widehat {W}=\varnothing $
, which is a contradiction to the fact that
$N_{G}[f]\cap \widehat {W}\subset N_{G^{\prime }}[f]\cap \widehat {W}=\varnothing $
, which is a contradiction to the fact that
![]() $\widehat {W}=W \setminus \{v\}$
is a vertex dominant set of G. Hence,
$\widehat {W}=W \setminus \{v\}$
is a vertex dominant set of G. Hence,
![]() $f=x_{1,i}x_{2,j}$
for some
$f=x_{1,i}x_{2,j}$
for some
![]() $i,j$
and
$i,j$
and
![]() $N_{G^{\prime }}[f]=N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] \cup \{X_{1} \cup X_{2}\}.$
This implies that
$N_{G^{\prime }}[f]=N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] \cup \{X_{1} \cup X_{2}\}.$
This implies that
![]() ${N_{G^{\prime }}[f] \cap \widehat {W}=(( N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] ) \cap \widehat {W}) \cup (\widehat {W}\cap X_{1})\kern1.3pt{=}\kern1.3pt\varnothing.}$
Consider an edge
${N_{G^{\prime }}[f] \cap \widehat {W}=(( N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] ) \cap \widehat {W}) \cup (\widehat {W}\cap X_{1})\kern1.3pt{=}\kern1.3pt\varnothing.}$
Consider an edge
![]() $f^{\prime }=x_{1},x_{1,i} \in E(G).$
Then
$f^{\prime }=x_{1},x_{1,i} \in E(G).$
Then
Note that
![]() $x_{1} \notin \widehat {W}$
, because otherwise
$x_{1} \notin \widehat {W}$
, because otherwise
![]() $N_{G^{\prime }}[f] \cap \widehat {W} \neq \varnothing ,$
which is a contradiction. Since
$N_{G^{\prime }}[f] \cap \widehat {W} \neq \varnothing ,$
which is a contradiction. Since
![]() $X_{1} \cap \widehat {W}=\varnothing $
and
$X_{1} \cap \widehat {W}=\varnothing $
and
![]() $N_{G}[x_{1,i}]\cap \widehat {W} \subset ( N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] ) \cap \widehat {W}=\varnothing ,$
Equation (3.1) gives
$N_{G}[x_{1,i}]\cap \widehat {W} \subset ( N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] ) \cap \widehat {W}=\varnothing ,$
Equation (3.1) gives
![]() $N_{G}[f^{\prime }] \cap \widehat {W}=\varnothing ,$
which is a contradiction. Hence,
$N_{G}[f^{\prime }] \cap \widehat {W}=\varnothing ,$
which is a contradiction. Hence,
![]() $\widehat {W}=W \setminus \{v\}$
is not a vertex dominant set in G.
$\widehat {W}=W \setminus \{v\}$
is not a vertex dominant set in G.
Lemma 3.8. With notation as in Notation 3.2, let W be a minimal vertex dominant set in
![]() $G^{\prime }$
such that
$G^{\prime }$
such that
![]() $W \cap X_{1} \neq \varnothing $
and
$W \cap X_{1} \neq \varnothing $
and
![]() $W_{1}=W \cup \{x_{2}\}$
. Let
$W_{1}=W \cup \{x_{2}\}$
. Let
![]() $\varnothing \neq T \subset W_{1}$
. If
$\varnothing \neq T \subset W_{1}$
. If
![]() $W_{1} \setminus T$
is a vertex dominant set in G, then
$W_{1} \setminus T$
is a vertex dominant set in G, then
![]() $|T|\leq 1$
.
$|T|\leq 1$
.
Proof. On the contrary, suppose that
![]() $|T|\geq 2$
. First we show that
$|T|\geq 2$
. First we show that
![]() $x_{2}\notin T$
. Using Lemma 3.7, we can see that if
$x_{2}\notin T$
. Using Lemma 3.7, we can see that if
![]() $x_{2}\in T$
, then
$x_{2}\in T$
, then
![]() $W_{1} \setminus T=W \setminus (T \setminus \{x_{2}\})$
is not a vertex dominant set in G. Thus,
$W_{1} \setminus T=W \setminus (T \setminus \{x_{2}\})$
is not a vertex dominant set in G. Thus,
![]() $x_{2}\notin T$
.
$x_{2}\notin T$
.
Let
![]() $y \in T \subset W.$
Since W is a minimal vertex dominant set of
$y \in T \subset W.$
Since W is a minimal vertex dominant set of
![]() $G^{\prime }$
, there exists an edge
$G^{\prime }$
, there exists an edge
![]() $f \in E(G^{\prime })$
such that
$f \in E(G^{\prime })$
such that
![]() $N_{G^{\prime }}[f] \cap W=\{y\}.$
Therefore,
$N_{G^{\prime }}[f] \cap W=\{y\}.$
Therefore,
![]() $N_{G^{\prime }}[f]\cap (W \setminus T)=\varnothing .$
If
$N_{G^{\prime }}[f]\cap (W \setminus T)=\varnothing .$
If
![]() $f \in E(G),$
then
$f \in E(G),$
then
![]() $\varnothing \neq N_{G}[f] \cap ( W_{1} \setminus T) \subset (N_{G^{\prime }}[f] \cap (W \setminus T)) \cup (N_{G}[f] \cap \{x_{2}\}).$
This implies that
$\varnothing \neq N_{G}[f] \cap ( W_{1} \setminus T) \subset (N_{G^{\prime }}[f] \cap (W \setminus T)) \cup (N_{G}[f] \cap \{x_{2}\}).$
This implies that
![]() $(N_{G}[f] \cap \{x_{2}\}) \neq \varnothing $
, and hence
$(N_{G}[f] \cap \{x_{2}\}) \neq \varnothing $
, and hence
![]() $x_{2} \in N_{G}[f],$
which means that
$x_{2} \in N_{G}[f],$
which means that
![]() $X_{1} \subset N_{G^{\prime }}[f].$
Thus,
$X_{1} \subset N_{G^{\prime }}[f].$
Thus,
![]() ${W\kern-1pt \cap\kern-1pt X_{1}\kern-1pt \subset\kern-1pt N_{G^{\prime }}[f]\kern-1pt \cap\kern-1pt W=\{y\}.}$
Since
${W\kern-1pt \cap\kern-1pt X_{1}\kern-1pt \subset\kern-1pt N_{G^{\prime }}[f]\kern-1pt \cap\kern-1pt W=\{y\}.}$
Since
![]() $W \cap X_{1} \neq \varnothing ,$
we have
$W \cap X_{1} \neq \varnothing ,$
we have
![]() $W\kern-1pt \cap\kern-1pt X_{1}=\{y\}$
. Let
$W\kern-1pt \cap\kern-1pt X_{1}=\{y\}$
. Let
![]() $y^{\prime } \in T\setminus \{y\}$
. Then
$y^{\prime } \in T\setminus \{y\}$
. Then
![]() $y^{\prime } \notin X_{1}.$
Now the fact that
$y^{\prime } \notin X_{1}.$
Now the fact that
![]() $W_{1} \setminus T$
is a vertex dominant set in G implies that
$W_{1} \setminus T$
is a vertex dominant set in G implies that
![]() $W_{1} \setminus \{y^{\prime }\}$
is a vertex dominant set in
$W_{1} \setminus \{y^{\prime }\}$
is a vertex dominant set in
![]() $G,$
which gives a contradiction to Lemma 3.6. If
$G,$
which gives a contradiction to Lemma 3.6. If
![]() $f \in E(G^{\prime })\setminus E(G)$
, then
$f \in E(G^{\prime })\setminus E(G)$
, then
![]() $X_{1} \subset N_{G^{\prime }}[f].$
Now proceeding as before,
$X_{1} \subset N_{G^{\prime }}[f].$
Now proceeding as before,
![]() $W_{1}\setminus \{ v\}$
is a vertex dominant set in G for some
$W_{1}\setminus \{ v\}$
is a vertex dominant set in G for some
![]() $v \notin X_{1} \cap \{x_{2}\}$
, which is a contradiction by Lemma 3.6.
$v \notin X_{1} \cap \{x_{2}\}$
, which is a contradiction by Lemma 3.6.
Proof of Proposition 3.3.
Let W be a minimal vertex dominating set of
![]() $G^{\prime }$
. If we have
$G^{\prime }$
. If we have
![]() $W \cap \{X_{1} \cup X_{2}\} =\varnothing $
, then by Lemma 3.4, W is a minimal vertex dominating set of G. Otherwise, using Lemma 3.5,
$W \cap \{X_{1} \cup X_{2}\} =\varnothing $
, then by Lemma 3.4, W is a minimal vertex dominating set of G. Otherwise, using Lemma 3.5,
![]() $W_{1}=W \cup \{x_{2}\}$
is a vertex dominating set of G. Further, by Lemma 3.8, either
$W_{1}=W \cup \{x_{2}\}$
is a vertex dominating set of G. Further, by Lemma 3.8, either
![]() $W_{1}=W \cup \{x_{2}\}$
is a minimal vertex dominating set of G or
$W_{1}=W \cup \{x_{2}\}$
is a minimal vertex dominating set of G or
![]() $W_{1} \setminus \{v\}$
is a minimal vertex dominating set of G for some
$W_{1} \setminus \{v\}$
is a minimal vertex dominating set of G for some
![]() $v \in W_{1}.$
It follows from the definition of
$v \in W_{1}.$
It follows from the definition of
![]() $\beta (G)$
that
$\beta (G)$
that
![]() $\beta (G^{\prime })\leq \beta (G).$
$\beta (G^{\prime })\leq \beta (G).$
To prove our main theorem, we shall use the following remark.
Remark 3.9. Let G be a bipartite graph and
![]() $s \geq 1$
be an integer. Then for every s-fold product
$s \geq 1$
be an integer. Then for every s-fold product
![]() $e_{1} \cdots e_{s}, $
the following statements hold.
$e_{1} \cdots e_{s}, $
the following statements hold.
-
(a) The ideal
 $(I(G)^{s+1} : e_{1} \cdots e_{s})$
is a quadratic square-free monomial ideal. Moreover, the graph
$(I(G)^{s+1} : e_{1} \cdots e_{s})$
is a quadratic square-free monomial ideal. Moreover, the graph
 $G^{\prime }$
associated to
$G^{\prime }$
associated to
 $(I(G)^{s+1} : e_{1} \cdots e_{s})$
is bipartite on the same vertex set and the same bipartition as G (see [Reference Alilooee and Banerjee1, Proposition 3.5]).
$(I(G)^{s+1} : e_{1} \cdots e_{s})$
is bipartite on the same vertex set and the same bipartition as G (see [Reference Alilooee and Banerjee1, Proposition 3.5]). -
(b) The ideal
 $I(G)^{s+1}:e_{1}\cdots e_{s}=(I(G)^{2}:e_{1})^{s}:e_{2}\cdots e_{s}$
(see [Reference Alilooee and Banerjee1, Lemma 3.7]).
$I(G)^{s+1}:e_{1}\cdots e_{s}=(I(G)^{2}:e_{1})^{s}:e_{2}\cdots e_{s}$
(see [Reference Alilooee and Banerjee1, Lemma 3.7]).
Note that if G is a triangle-free graph, then the graph H associated to
![]() $I(G)^{2}:e$
need not be a triangle-free graph, for
$I(G)^{2}:e$
need not be a triangle-free graph, for
![]() $e \in E(G)$
. Thus, in view of Remark 3.9(a), we prove the following result for bipartite graphs.
$e \in E(G)$
. Thus, in view of Remark 3.9(a), we prove the following result for bipartite graphs.
Corollary 3.10. Let G be a bipartite graph and u be a minimal monomial generator of
![]() $I(G)^{s}$
. Then
$I(G)^{s}$
. Then
![]() $\beta (G^{\prime }) \leq \beta (G),$
where
$\beta (G^{\prime }) \leq \beta (G),$
where
![]() $G^{\prime }$
is the graph associated to
$G^{\prime }$
is the graph associated to
![]() $I(G)^{s+1}:u$
.
$I(G)^{s+1}:u$
.
Proof. We use induction on s. For
![]() $s=1$
, the result follows from Proposition 3.3. Assume that
$s=1$
, the result follows from Proposition 3.3. Assume that
![]() $s>1$
. Let
$s>1$
. Let
![]() $u=e_{1}\cdots e_{s}$
for some edges
$u=e_{1}\cdots e_{s}$
for some edges
![]() $e_{1}, \ldots , e_{s}$
in the edge set
$e_{1}, \ldots , e_{s}$
in the edge set
![]() $E(G)$
. If H is the graph associated to
$E(G)$
. If H is the graph associated to
![]() $I(G)^{2}:e_{1}$
, then by Proposition 3.3,
$I(G)^{2}:e_{1}$
, then by Proposition 3.3,
![]() $\beta (H)\leq \beta (G).$
By Remark 3.9, the graph H is a bipartite graph and
$\beta (H)\leq \beta (G).$
By Remark 3.9, the graph H is a bipartite graph and
![]() $I(G)^{s+1}:e_{1}\cdots e_{s}=I(H)^{s}:e_{2}\cdots e_{s}$
. Hence, by induction, we get
$I(G)^{s+1}:e_{1}\cdots e_{s}=I(H)^{s}:e_{2}\cdots e_{s}$
. Hence, by induction, we get
![]() $\beta (G^{\prime })\leq \beta (H)\leq \beta (G)$
.
$\beta (G^{\prime })\leq \beta (H)\leq \beta (G)$
.
Now we are ready to prove our main theorem.
Theorem 3.11. Let G be a bipartite graph and
![]() $I(G)$
be its edge ideal. Then
$I(G)$
be its edge ideal. Then
![]() $\mathrm {reg}(S/I(G)^{s+1} ) \leq 2s+\beta (G)$
for all
$\mathrm {reg}(S/I(G)^{s+1} ) \leq 2s+\beta (G)$
for all
![]() $s \geq 0$
.
$s \geq 0$
.
Proof. We use induction on s. For
![]() $s=0$
, the result follows from [Reference Bıyıkoğlu and Civan4, Theorem 3.19]. Now assume that
$s=0$
, the result follows from [Reference Bıyıkoğlu and Civan4, Theorem 3.19]. Now assume that
![]() $s\ge 1$
. In view of Theorem 2.6, it is enough to prove that
$s\ge 1$
. In view of Theorem 2.6, it is enough to prove that
for all minimal monomial generators u of
![]() $I(G)^{s}$
. Let
$I(G)^{s}$
. Let
![]() $G^{\prime }$
be the graph associated to
$G^{\prime }$
be the graph associated to
![]() $(I(G)^{s+1} : u)$
. Now, the proof follows from Corollary 3.10 and [Reference Bıyıkoğlu and Civan4, Theorem 3.19].
$(I(G)^{s+1} : u)$
. Now, the proof follows from Corollary 3.10 and [Reference Bıyıkoğlu and Civan4, Theorem 3.19].
4 Bipartite Kneser graphs
Theorem 4.1 (Frankl, [Reference Frankl6]).
Suppose
![]() $\mathcal {A}=\{A_{1},\ldots , A_{l}\}$
is a family of r-sets and
$\mathcal {A}=\{A_{1},\ldots , A_{l}\}$
is a family of r-sets and
![]() $\mathcal {B}=\{B_{1},\ldots , B_{l}\}$
is a family of s-sets such that:
$\mathcal {B}=\{B_{1},\ldots , B_{l}\}$
is a family of s-sets such that:
-
(i)
 $A_{i} \cap B_{i}=\varnothing $
for
$A_{i} \cap B_{i}=\varnothing $
for
 $1 \leq i \leq m$
;
$1 \leq i \leq m$
; -
(ii)
 $A_{i} \cap B_{j} \neq \varnothing $
for
$A_{i} \cap B_{j} \neq \varnothing $
for
 $1 \leq i<j\leq m.$
$1 \leq i<j\leq m.$
Then
 $$ \begin{align*}l \leq \binom{r+s}{s}.\end{align*} $$
$$ \begin{align*}l \leq \binom{r+s}{s}.\end{align*} $$
Proposition 4.2. Let
![]() $G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then
$G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then
![]() $\beta (G) \leq \binom {2k}{k}.$
$\beta (G) \leq \binom {2k}{k}.$
Proof. Let
![]() $W=\{C_{1},\ldots ,C_{t},C_{t+1},\ldots ,C_{m}\}$
be a minimal vertex dominant set in G, where
$W=\{C_{1},\ldots ,C_{t},C_{t+1},\ldots ,C_{m}\}$
be a minimal vertex dominant set in G, where
![]() $C_{i} \in [n]^{(k)}, 1 \leq i \leq t$
, and
$C_{i} \in [n]^{(k)}, 1 \leq i \leq t$
, and
![]() $C_{i} \in [n]^{(n-k)}, t+1 \leq i \leq m.$
Since W is a minimal vertex dominant set in G, for each vertex
$C_{i} \in [n]^{(n-k)}, t+1 \leq i \leq m.$
Since W is a minimal vertex dominant set in G, for each vertex
![]() $C_{i} \in W$
, there exists a vertex
$C_{i} \in W$
, there exists a vertex
![]() $D_{i}$
such that
$D_{i}$
such that
![]() $N_{G}(D_{i})\cap W=\{C_{i}\}$
. This implies that
$N_{G}(D_{i})\cap W=\{C_{i}\}$
. This implies that
 $$ \begin{align*} C_{i} \subset D_{j} &\quad \text{if and only if } i=j,\quad 1\leq i,j \leq t \\ C_{j} \supset D_{i} &\quad \text{if and only if } i=j,\quad t+1\leq i,j \leq m. \end{align*} $$
$$ \begin{align*} C_{i} \subset D_{j} &\quad \text{if and only if } i=j,\quad 1\leq i,j \leq t \\ C_{j} \supset D_{i} &\quad \text{if and only if } i=j,\quad t+1\leq i,j \leq m. \end{align*} $$
Therefore,
 $$ \begin{align*} C_{i} \cap D_{j}^{c}=\phi &\quad \text{if and only if } i=j,\quad 1\leq i,j \leq t \\ C_{j}^{c}\cap D_{i}=\phi &\quad \text{if and only if } i=j,\quad t+1\leq i,j \leq m. \end{align*} $$
$$ \begin{align*} C_{i} \cap D_{j}^{c}=\phi &\quad \text{if and only if } i=j,\quad 1\leq i,j \leq t \\ C_{j}^{c}\cap D_{i}=\phi &\quad \text{if and only if } i=j,\quad t+1\leq i,j \leq m. \end{align*} $$
Consider the collection
![]() $W^{\prime }=\{(X_{1},Y_{1}),\ldots ,(X_{m},Y_{m})\}$
of ordered pairs, where
$W^{\prime }=\{(X_{1},Y_{1}),\ldots ,(X_{m},Y_{m})\}$
of ordered pairs, where
![]() $X_{i}=C_{i},Y_{i}=D_{i}^{c}$
for
$X_{i}=C_{i},Y_{i}=D_{i}^{c}$
for
![]() $1\leq i \leq t$
and
$1\leq i \leq t$
and
![]() $X_{i}=D_{i},Y_{i}=C_{i}^{c}$
for
$X_{i}=D_{i},Y_{i}=C_{i}^{c}$
for
![]() $ t+1\leq i \leq m$
. By the choice of the collection
$ t+1\leq i \leq m$
. By the choice of the collection
![]() $W^{\prime }$
, it is clear that
$W^{\prime }$
, it is clear that
![]() $X_{i}\cap Y_{i}=\varnothing $
for all i, and
$X_{i}\cap Y_{i}=\varnothing $
for all i, and
![]() $X_{i}\cap Y_{j}\neq \varnothing $
for
$X_{i}\cap Y_{j}\neq \varnothing $
for
![]() $1\leq i<j\leq t$
and
$1\leq i<j\leq t$
and
![]() $t+1\leq i<j\leq m$
. Now, since W is an independent set,
$t+1\leq i<j\leq m$
. Now, since W is an independent set,
![]() $C_{i}\not \subset C_{j}$
and hence
$C_{i}\not \subset C_{j}$
and hence
![]() $C_{i}\cap C_{j}^{c}\neq \varnothing $
for all
$C_{i}\cap C_{j}^{c}\neq \varnothing $
for all
![]() $i\neq j$
. Therefore,
$i\neq j$
. Therefore,
![]() $X_{i}\cap Y_{j}\neq \varnothing $
for
$X_{i}\cap Y_{j}\neq \varnothing $
for
![]() $1\leq i\leq t$
and
$1\leq i\leq t$
and
![]() $t+1\leq j\leq m$
. This implies that
$t+1\leq j\leq m$
. This implies that
![]() $X_{i}\cap Y_{j}\neq \varnothing $
for
$X_{i}\cap Y_{j}\neq \varnothing $
for
![]() $1\leq i<j\leq m$
and
$1\leq i<j\leq m$
and
![]() $X_{i}\cap Y_{i}= \varnothing $
for
$X_{i}\cap Y_{i}= \varnothing $
for
![]() $1\leq i\leq m.$
Since
$1\leq i\leq m.$
Since
![]() $|X_{i}|=|Y_{i}|=k$
for all i, in view of Theorem 4.1, we get
$|X_{i}|=|Y_{i}|=k$
for all i, in view of Theorem 4.1, we get
![]() $m \leq \binom {2k}{k}$
.
$m \leq \binom {2k}{k}$
.
Corollary 4.3. For
![]() $m\geq 2k+1$
, let
$m\geq 2k+1$
, let
![]() $G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then the induced matching number of G is given by
$G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then the induced matching number of G is given by
![]() $\nu (G) = \binom {2k}{k}.$
$\nu (G) = \binom {2k}{k}.$
Proof. In view of [Reference Katzman10, Lemma 2.2] and [Reference Bıyıkoğlu and Civan4, Theorem 3.19],
Using [Reference Kumar, Singh and Verma12, Lemma 4.2],
![]() $\nu (G) \geq \binom {2k}{k}$
. Now, by Proposition 4.2,
$\nu (G) \geq \binom {2k}{k}$
. Now, by Proposition 4.2,
![]() $\nu (G)=\binom {2k}{k}.$
$\nu (G)=\binom {2k}{k}.$
Corollary 4.4. For
![]() $m\geq 2k+1$
, let
$m\geq 2k+1$
, let
![]() $G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then, for all
$G=\mathcal {H}(m,k)$
be the bipartite Kneser graph. Then, for all
![]() $s>0$
,
$s>0$
,
![]() $ \mathrm {reg}(S/I(G)^{s} )=2(s-1)+\binom {2k}{k}.$
$ \mathrm {reg}(S/I(G)^{s} )=2(s-1)+\binom {2k}{k}.$
Proof. From [Reference Beyarslan, Hà and Trung3, Theorem 4.5] and Corollary 4.3,
![]() $ \mathrm {reg}(S/I(G)^{s} ) \geq 2(s-1)+\binom {2k}{k}.$
Now, by Theorem 3.11 and Proposition 4.2,
$ \mathrm {reg}(S/I(G)^{s} ) \geq 2(s-1)+\binom {2k}{k}.$
Now, by Theorem 3.11 and Proposition 4.2,
![]() $ \mathrm {reg}(S/I(G)^{s} ) \leq 2(s-1)+\binom {2k}{k},$
and hence we get the desired result.
$ \mathrm {reg}(S/I(G)^{s} ) \leq 2(s-1)+\binom {2k}{k},$
and hence we get the desired result.