Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T17:34:23.927Z Has data issue: false hasContentIssue false
  • English
  • Français

REFLEXIVE INDEX OF A FAMILY OF SUBSPACES

Part of: General theory of linear operators

Published online by Cambridge University Press:  02 April 2014

W. E. LONGSTAFF
W. E. LONGSTAFF*
Affiliation:
11 Tussock Crescent, Elanora, Queensland 4221, Australia email longstaf10@bigpond.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A definition of the reflexive index of a family of (closed) subspaces of a complex, separable Hilbert space 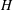$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ is given, analogous to one given by D. Zhao for a family of subsets of a set. 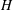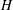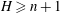Following some observations, some examples are given, including: (a) a subspace lattice on $H$ with precisely five nontrivial elements with infinite reflexive index; (b) a reflexive subspace lattice on $H$ with infinite reflexive index; (c) for each positive integer $n$ satisfying dim $H\ge n+1$, a reflexive subspace lattice on 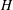$H$ with reflexive index $n$. If 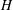$H$ is infinite-dimensional and 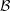${\mathcal{B}}$ is an atomic Boolean algebra subspace lattice on 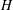$H$ with $n$ equidimensional atoms and with the property that the vector sum 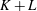$K+L$ is closed, for every 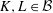$K,L\in {\mathcal{B}}$, then 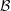${\mathcal{B}}$ has reflexive index at most $n$.

Keywords

reflexivesubspaceinvariant

MSC classification

Secondary: 47A15: Invariant subspaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 1 , August 2014 , pp. 134 - 140
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Arveson, W. B., ‘Operator algebras and invariant subspaces’, Ann. of Math. 103(2) (1974), 433–532.CrossRefGoogle Scholar
Hadwin, D. W., Longstaff, W. E. and Rosenthal, P., ‘Small transitive lattices’, Proc. Amer. Math. Soc. 87(1) (1983), 121–124.Google Scholar
Halmos, P. R., ‘Ten problems in Hilbert space’, Bull. Amer. Math. Soc. 76 (1970), 887–933.CrossRefGoogle Scholar
Halmos, P. R., ‘Reflexive lattices of subspaces’, J. Lond. Math. Soc. 4(2) (1971), 257–263.CrossRefGoogle Scholar
Harrison, K. J., On Lattices of Invariant Subspaces, Doctoral Thesis (Monash University, Melbourne), 1970.Google Scholar
Harrison, K. J. and Longstaff, W. E., ‘Reflexive subspace lattices in finite-dimensional Hilbert spaces’, Indiana Univ. Math. J. 26(6) (1977), 1019–1025.CrossRefGoogle Scholar
Harrison, K. J. and Longstaff, W. E., ‘An invariant subspace lattice of order-type ω + ω + 1’, Proc. Amer. Math. Soc. 79(1) (1980), 45–49.Google Scholar
Harrison, K. J. and Longstaff, W. E., ‘Automorphic images of commutative subspace lattices’, Proc. Amer. Math. Soc. 296 (1986), 217–228.CrossRefGoogle Scholar
Harrison, K. J., Radjavi, H. and Rosenthal, P., ‘A transitive medial subspace lattice’, Proc. Amer. Math. Soc. 28 (1971), 119–121.Google Scholar
Lambrou, M. S. and Longstaff, W. E., ‘Abelian algebras and reflexive lattices’, Bull. Lond. Math. Soc. 12 (1980), 165–168.Google Scholar
Lambrou, M. S. and Longstaff, W. E., ‘Nonreflexive pentagon subspace lattices’, Studia Math. 125(2) (1997), 187–199.CrossRefGoogle Scholar
Laurie, C. and Longstaff, W. E., ‘A note on rank-one operators in reflexive algebras’, Proc. Amer. Math. Soc. 89(2) (1983), 293–297.CrossRefGoogle Scholar
Longstaff, W. E., ‘Generators of nest algebras’, Canad. J. Math. 26 (1974), 565–575.CrossRefGoogle Scholar
Longstaff, W. E., ‘Strongly reflexive subspace lattices’, J. Lond. Math. Soc. 11(2) (1975), 491–498.Google Scholar
Longstaff, W. E., ‘Nonreflexive double triangles’, J. Aust. Math. Soc. Ser. A 35 (1983), 349–356.Google Scholar
Longstaff, W. E., ‘On lattices whose every realization on Hilbert space is reflexive’, J. Lond. Math. Soc. 37(2) (1988), 499–508.CrossRefGoogle Scholar
Longstaff, W. E., Nation, J. B. and Panaia, O., ‘Abstract reflexive sublattices and completely distributive collapsibility’, Bull. Aust. Math. Soc. 58 (1998), 245–260.CrossRefGoogle Scholar
Longstaff, W. E. and Rosenthal, P., ‘On two questions of Halmos concerning subspace lattices’, Proc. Amer. Math. Soc. 75 (1979), 85–86.CrossRefGoogle Scholar
Radjavi, H. and Rosenthal, P., Invariant Subspaces, 2nd edn (Dover, 2003).Google Scholar
Ringrose, J. R., ‘On some algebras of operators’, Proc. Lond. Math. Soc. 15 (1965), 61–83.Google Scholar
Zhao, D., ‘Reflexive index of a family of sets’, Kyungpook Math. J., to appear.Google Scholar