 $\lowercase {X}^{\lowercase {M}}$ AND
$\lowercase {X}^{\lowercase {M}}$ AND  $\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
$\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUPPublished online by Cambridge University Press: 02 August 2012
In a recent article [K. H. Hofmann and F. G. Russo, ‘The probability that  $x$ and
$x$ and 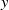 $y$ commute in a compact group’, Math. Proc. Cambridge Phil Soc., to appear] we calculated for a compact group
$y$ commute in a compact group’, Math. Proc. Cambridge Phil Soc., to appear] we calculated for a compact group  $G$ the probability
$G$ the probability 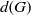 $d(G)$ that two randomly selected elements
$d(G)$ that two randomly selected elements  $x, y\in G$ satisfy
$x, y\in G$ satisfy  $xy=yx$, and we discussed the remarkable consequences on the structure of
$xy=yx$, and we discussed the remarkable consequences on the structure of 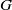 $G$ which follow from the assumption that
$G$ which follow from the assumption that 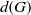 $d(G)$ is positive. In this note we consider two natural numbers
$d(G)$ is positive. In this note we consider two natural numbers 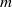 $m$ and
$m$ and  $n$ and the probability
$n$ and the probability  $d_{m,n}(G)$ that for two randomly selected elements
$d_{m,n}(G)$ that for two randomly selected elements  $x, y\in G$ the relation
$x, y\in G$ the relation 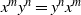 $x^my^n=y^nx^m$ holds. The situation is more complicated whenever
$x^my^n=y^nx^m$ holds. The situation is more complicated whenever 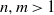 $n,m\gt 1$. If
$n,m\gt 1$. If 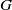 $G$ is a compact Lie group and if its identity component
$G$ is a compact Lie group and if its identity component 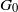 $G_0$ is abelian, then it follows readily that
$G_0$ is abelian, then it follows readily that 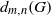 $d_{m,n}(G)$ is positive. We show here that the following condition suffices for the converse to hold in an arbitrary compact group
$d_{m,n}(G)$ is positive. We show here that the following condition suffices for the converse to hold in an arbitrary compact group  $G$: for any nonopen closed subgroup
$G$: for any nonopen closed subgroup  $H$ of
$H$ of 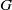 $G$, the sets
$G$, the sets 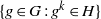 $\{g\in G: g^k\in H\}$ for both
$\{g\in G: g^k\in H\}$ for both 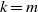 $k=m$ and
$k=m$ and  $k=n$ have Haar measure
$k=n$ have Haar measure  $0$. Indeed, we show that if a compact group
$0$. Indeed, we show that if a compact group  $G$ satisfies this condition and if
$G$ satisfies this condition and if  $d_{m,n}(G)\gt 0$, then the identity component of
$d_{m,n}(G)\gt 0$, then the identity component of  $G$is abelian.
$G$is abelian.