Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-04T19:44:14.307Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMAL STOPPING FOR THE LAST EXIT TIME

Part of: Markov processes Inference from stochastic processes Stochastic processes

Published online by Cambridge University Press:  04 October 2018

DAN REN Open the ORCID record for DAN REN [Opens in a new window]
DAN REN*
Affiliation:
Department of Mathematics, University of Dayton, Dayton, OH 45469, USA email dren01@udayton.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a one-dimensional downwards transient diffusion process 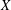$X$, we consider a random time $\unicode[STIX]{x1D70C}$, the last exit time when $X$ exits a certain level 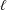$\ell$, and detect the optimal stopping time for it. In particular, for this random time 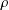$\unicode[STIX]{x1D70C}$, we solve the optimisation problem 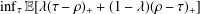$\inf _{\unicode[STIX]{x1D70F}}\mathbb{E}[\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70C})_{+}+(1-\unicode[STIX]{x1D706})(\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70F})_{+}]$ over all stopping times $\unicode[STIX]{x1D70F}$. We show that the process should stop optimally when it runs below some fixed level 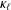$\unicode[STIX]{x1D705}_{\ell }$ for the first time, where $\unicode[STIX]{x1D705}_{\ell }$ is the unique solution in the interval 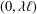$(0,\unicode[STIX]{x1D706}\ell )$ of an explicitly defined equation.

Keywords

optimal stoppingrandom timedownwards transient diffusionlast exit time

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 62M20: Prediction 60J65: Brownian motion
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 148 - 160
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Baurdoux, E. J. and Pedraza, J., ‘Predicting the last zero of a spectrally negative Lévy process’, Preprint, 2018, arXiv:1805.12190.Google Scholar
Glover, K. and Hulley, H., ‘Optimal prediction of the last-passage time of a transient diffusion’, SIAM J. Control Optim. 52 (2014), 3833–3853.Google Scholar
Karatzas, I. and Shreve, S. E., Brownian Motion and Stochastic Calculus, 2nd edn, Graduate Texts in Mathematics, 113 (Springer, New York, 1991).Google Scholar
Nikeghbali, A. and Yor, M., ‘Doob’s maximal identity, multiplicative decompositions and enlargements of filtrations’, Illinois J. Math. 50 (2006), 791–814.Google Scholar
Peskir, G., ‘Optimal detection of a hidden target: the median rule’, Stochastic Process. Appl. 122 (2012), 2249–2263.Google Scholar
Du Toit, J., Peskir, G. and Shiryaev, A., ‘Predicting the last zero of Brownian motion with drift’, Stochastics 80 (2008), 229–245.Google Scholar
Urusov, M. A., ‘On a property of the moment at which Brownian motion attains its maximum and some optimal stopping problems’, Theory Probab. Appl. 49 (2005), 169–176.Google Scholar