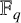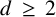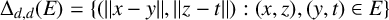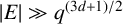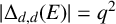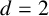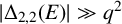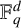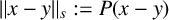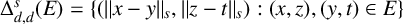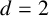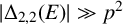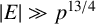1 Introduction
The general Erdős distance problem is to determine the number of distinct distances spanned by a finite set of points. In the Euclidean space, it is conjectured that for any finite set
![]() $E \subset \mathbb {R}^d$
,
$E \subset \mathbb {R}^d$
,
![]() $d\ge 2$
, we have
$d\ge 2$
, we have
![]() $|\Delta (E)| \gtrapprox |E|^{{2}/{d}}$
, where
$|\Delta (E)| \gtrapprox |E|^{{2}/{d}}$
, where
![]() $\Delta (E)=\{\|x-y\| : x,y \in E\}$
. Here and throughout,
$\Delta (E)=\{\|x-y\| : x,y \in E\}$
. Here and throughout,
![]() $X\ll Y$
means that there exists
$X\ll Y$
means that there exists
![]() $C>0$
such that
$C>0$
such that
![]() $X\le CY$
, and
$X\le CY$
, and
![]() $X\lessapprox Y$
with the parameter N means that for any
$X\lessapprox Y$
with the parameter N means that for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $C_{\varepsilon }>0$
such that
$C_{\varepsilon }>0$
such that
![]() $X\,\le \,C_{\varepsilon }N^{\varepsilon }Y$
.
$X\,\le \,C_{\varepsilon }N^{\varepsilon }Y$
.
The finite field analogue of the distance problem was first studied by Bourgain et al. [Reference Bourgain, Katz and Tao2] over prime fields. In this setting, the Euclidean distance between any two points
![]() $x=(x_1,\ldots , x_d), y=(y_1,\ldots ,y_d) \in \mathbb {F}_q^d$
, the d-dimensional vector space over the finite field
$x=(x_1,\ldots , x_d), y=(y_1,\ldots ,y_d) \in \mathbb {F}_q^d$
, the d-dimensional vector space over the finite field
![]() $\mathbb F_q$
of order q, is
$\mathbb F_q$
of order q, is
![]() $\|x-y\|=\sum _{i=1}^d(x_i-y_i)^2\in \mathbb F_q$
. For prime fields
$\|x-y\|=\sum _{i=1}^d(x_i-y_i)^2\in \mathbb F_q$
. For prime fields
![]() $\mathbb {F}_p$
with
$\mathbb {F}_p$
with
![]() $p\equiv 1 \pmod 4$
, they showed that if
$p\equiv 1 \pmod 4$
, they showed that if
![]() $E \subset \mathbb {F}_p^2$
with
$E \subset \mathbb {F}_p^2$
with
![]() $|E|=p^{\delta }$
for some
$|E|=p^{\delta }$
for some
![]() $0<\delta <2$
, then the distance set satisfies
$0<\delta <2$
, then the distance set satisfies
![]() $|\Delta (E)| \gg |E|^{{1}/{2}+\varepsilon }$
for some
$|\Delta (E)| \gg |E|^{{1}/{2}+\varepsilon }$
for some
![]() $\varepsilon>0$
depending only on
$\varepsilon>0$
depending only on
![]() $\delta $
.
$\delta $
.
This bound does not hold in general for arbitrary finite fields
![]() $\mathbb {F}_q$
, as shown by Iosevich and Rudnev [Reference Iosevich and Rudnev9]. In this general setting, they considered the Erdős–Falconer distance problem to determine how large
$\mathbb {F}_q$
, as shown by Iosevich and Rudnev [Reference Iosevich and Rudnev9]. In this general setting, they considered the Erdős–Falconer distance problem to determine how large
![]() $E \subset \mathbb {F}_q^d$
needs to be so that
$E \subset \mathbb {F}_q^d$
needs to be so that
![]() $\Delta (E)$
spans all possible distances or at least a positive proportion of them. More precisely, they proved that
$\Delta (E)$
spans all possible distances or at least a positive proportion of them. More precisely, they proved that
![]() $\Delta (E)=\mathbb {F}_q$
if
$\Delta (E)=\mathbb {F}_q$
if
![]() $|E|> 2q^{{(d+1)}/{2}}$
in the all distances case, and also conjectured that
$|E|> 2q^{{(d+1)}/{2}}$
in the all distances case, and also conjectured that
![]() $|\Delta (E)| \gg q$
if
$|\Delta (E)| \gg q$
if
![]() $|E| \gg _{\varepsilon } q^{{d}/{2}+\varepsilon }$
in the positive proportion case. In [Reference Hart, Iosevich, Koh and Rudnev6], it was shown that the exponent in the all distances case is sharp for odd d, and the conjecture for the positive proportion case holds for all
$|E| \gg _{\varepsilon } q^{{d}/{2}+\varepsilon }$
in the positive proportion case. In [Reference Hart, Iosevich, Koh and Rudnev6], it was shown that the exponent in the all distances case is sharp for odd d, and the conjecture for the positive proportion case holds for all
![]() $E \subset \{x\in \mathbb {F}_q^d : \|x\|=1\}$
. It is conjectured that in even dimensions, the optimal exponent is
$E \subset \{x\in \mathbb {F}_q^d : \|x\|=1\}$
. It is conjectured that in even dimensions, the optimal exponent is
![]() ${d}/{2}$
for the all distances case. In particular for
${d}/{2}$
for the all distances case. In particular for
![]() $d=2$
, it was shown in [Reference Chapman, Erdogan, Hart, Iosevich and Koh3] that if
$d=2$
, it was shown in [Reference Chapman, Erdogan, Hart, Iosevich and Koh3] that if
![]() $E \subseteq \mathbb {F}_q^2$
satisfies
$E \subseteq \mathbb {F}_q^2$
satisfies
![]() $|E| \gg q^{{4}/{3}}$
, then
$|E| \gg q^{{4}/{3}}$
, then
![]() $|\Delta (E)| \gg q$
, improving the positive proportion case. The proofs in [Reference Chapman, Erdogan, Hart, Iosevich and Koh3] use extension estimates for circles. Therefore, one would expect to get improvements for distance problems if one can obtain improved estimates for extension problems.
$|\Delta (E)| \gg q$
, improving the positive proportion case. The proofs in [Reference Chapman, Erdogan, Hart, Iosevich and Koh3] use extension estimates for circles. Therefore, one would expect to get improvements for distance problems if one can obtain improved estimates for extension problems.
There have been a recent series of other improvements and generalisations on the Erdős–Falconer distance problem. In [Reference Hieu and Pham7], a generalisation for subsets of regular varieties was studied. Extension theorems and their connection to the Erdős–Falconer problem are the main focus of [Reference Koh, Pham and Vinh10]. The exponents
![]() ${(d+1)}/{2}$
and
${(d+1)}/{2}$
and
![]() ${d}/{2}$
were improved in [Reference Pham and Suk13, Reference Pham and Vinh14] for subsets E with Cartesian product structure in the all distances case for
${d}/{2}$
were improved in [Reference Pham and Suk13, Reference Pham and Vinh14] for subsets E with Cartesian product structure in the all distances case for
![]() $|\Delta (E)|$
and in the positive proportion case for the quotient distance set
$|\Delta (E)|$
and in the positive proportion case for the quotient distance set
![]() $|{\Delta (E)}/{\Delta (E)}|$
.
$|{\Delta (E)}/{\Delta (E)}|$
.
A two-parameter variant of the Erdős–Falconer distance problem for the Euclidean distance was studied by Birklbauer and Iosevich in [Reference Birklbauer and Iosevich1]. More precisely, given
![]() $E \subseteq \mathbb {F}_q^d \times \mathbb {F}_q^d$
, where
$E \subseteq \mathbb {F}_q^d \times \mathbb {F}_q^d$
, where
![]() $d\ge 2$
, define the two-parameter distance set as
$d\ge 2$
, define the two-parameter distance set as
They proved the following results.
Theorem 1.1 [Reference Birklbauer and Iosevich1]
Let E be a subset in
![]() $\mathbb {F}_q^d \times \mathbb {F}_q^d$
. If
$\mathbb {F}_q^d \times \mathbb {F}_q^d$
. If
![]() $|E| \gg q^{{(3d+1)}/{2}}$
, then
$|E| \gg q^{{(3d+1)}/{2}}$
, then
![]() $ |\Delta _{d, d}(E)| = q^2$
.
$ |\Delta _{d, d}(E)| = q^2$
.
Theorem 1.2 [Reference Birklbauer and Iosevich1]
Let E be a subset in
![]() $\mathbb {F}_q^2 \times \mathbb {F}_q^2$
. If
$\mathbb {F}_q^2 \times \mathbb {F}_q^2$
. If
![]() $|E| \gg q^{{10}/{3}}$
, then
$|E| \gg q^{{10}/{3}}$
, then
![]() $ |\Delta _{2, 2}(E)| \gg q^2$
.
$ |\Delta _{2, 2}(E)| \gg q^2$
.
In this short note, we provide an extension and an improvement of these results. Unlike [Reference Birklbauer and Iosevich1], which relies heavily on Fourier analytic techniques, we use an elementary counting approach.
Let
![]() $P(x)=\sum _{i=1}^da_ix_i^s\in \mathbb F_q[x_1,\ldots , x_d]$
be a fixed diagonal polynomial in d variables of degree
$P(x)=\sum _{i=1}^da_ix_i^s\in \mathbb F_q[x_1,\ldots , x_d]$
be a fixed diagonal polynomial in d variables of degree
![]() $s\ge 2$
. For
$s\ge 2$
. For
![]() $x=(x_1,\ldots ,x_d), y=(y_1,\ldots ,y_d) \in \mathbb {F}_q^d$
, we introduce
$x=(x_1,\ldots ,x_d), y=(y_1,\ldots ,y_d) \in \mathbb {F}_q^d$
, we introduce
 $$ \begin{align*} \|x-y\|_s:=P(x-y)=\sum_{i=1}^d a_i(x_i-y_i)^s\in\mathbb F_q. \end{align*} $$
$$ \begin{align*} \|x-y\|_s:=P(x-y)=\sum_{i=1}^d a_i(x_i-y_i)^s\in\mathbb F_q. \end{align*} $$
For any set
![]() $E\subset \mathbb {F}_q^d\times \mathbb {F}_q^d$
, define
$E\subset \mathbb {F}_q^d\times \mathbb {F}_q^d$
, define
Our first result reads as follows.
Theorem 1.3. Let E be a subset in
![]() $\mathbb {F}_q^d \times \mathbb {F}_q^d$
. If
$\mathbb {F}_q^d \times \mathbb {F}_q^d$
. If
![]() $|E| \gg q^{{(3d+1)}/{2}}$
, then
$|E| \gg q^{{(3d+1)}/{2}}$
, then
![]() $ |\Delta _{d, d}^s(E)| \gg q^2$
.
$ |\Delta _{d, d}^s(E)| \gg q^2$
.
Our method also works for the multi-parameter distance set for
![]() $E \subseteq \mathbb {F}_q^{d_1+\cdots +d_k}$
, but we do not discuss such extensions here. For
$E \subseteq \mathbb {F}_q^{d_1+\cdots +d_k}$
, but we do not discuss such extensions here. For
![]() $d=2$
, we get an improved version of Theorem 1.2 for the Euclidean distance function over prime fields.
$d=2$
, we get an improved version of Theorem 1.2 for the Euclidean distance function over prime fields.
Theorem 1.4. Let
![]() $E \subseteq \mathbb {F}_p^2 \times \mathbb {F}_p^2$
. If
$E \subseteq \mathbb {F}_p^2 \times \mathbb {F}_p^2$
. If
![]() $|E| \gg p^{{13}{/4}}$
, then
$|E| \gg p^{{13}{/4}}$
, then
![]() $ |\Delta _{2,2}(E)| \gg p^2$
.
$ |\Delta _{2,2}(E)| \gg p^2$
.
The continuous versions of Theorems 1.3 and 1.4 have been studied in [Reference Du, Ou and Zhang4, Reference Hambrook, Iosevich and Rice5, Reference Iosevich, Janczak and Passant8]. We do not know whether our method can be extended to that setting. It follows from our approach that the conjectured exponent
![]() ${d}/{2}$
of the (one-parameter) distance problem would imply the sharp exponent for the two-parameter analogue, namely
${d}/{2}$
of the (one-parameter) distance problem would imply the sharp exponent for the two-parameter analogue, namely
![]() ${3d}/{2}$
, for even dimensions. We refer to [Reference Birklbauer and Iosevich1] for constructions and more discussions.
${3d}/{2}$
, for even dimensions. We refer to [Reference Birklbauer and Iosevich1] for constructions and more discussions.
2 Proof of Theorem 1.3
By using the following auxiliary result whose proof relies on Fourier analytic methods (see [Reference Vinh15, Theorem 2.3] and [Reference Koh and Shen11, Corollaries 3.1 and 3.4]), we are able to give an elegant proof for Theorem 1.3. Compared with the method in [Reference Birklbauer and Iosevich1], ours is more elementary.
Lemma 2.1. Let
![]() $X, Y \subseteq \mathbb {F}_q^d$
. Define
$X, Y \subseteq \mathbb {F}_q^d$
. Define
![]() $\Delta ^s(X, Y)=\{\|x-y\|_s\colon x\in X, y\in Y\}$
. If
$\Delta ^s(X, Y)=\{\|x-y\|_s\colon x\in X, y\in Y\}$
. If
![]() $|X||Y|\gg q^{d+1}$
, then
$|X||Y|\gg q^{d+1}$
, then
![]() $|\Delta ^s(X, Y)|\gg q$
.
$|\Delta ^s(X, Y)|\gg q$
.
Proof of Theorem 1.3
By assumption,
![]() $|E|\ge Cq^{d+{(d+1)}/{2}}$
for some constant
$|E|\ge Cq^{d+{(d+1)}/{2}}$
for some constant
![]() $C>0$
. For
$C>0$
. For
![]() $y\in \mathbb {F}_q^d$
, let
$y\in \mathbb {F}_q^d$
, let
![]() $E_y:=\{x\in \mathbb F_q^d : (x, y)\in E\}$
and define
$E_y:=\{x\in \mathbb F_q^d : (x, y)\in E\}$
and define
We first show that
![]() $ |Y|\,\ge \, \tfrac 12C q^{{(d+1)}/{2}}$
. Note that
$ |Y|\,\ge \, \tfrac 12C q^{{(d+1)}/{2}}$
. Note that
 $$ \begin{align*}|E|=\sum_{y \in Y} |E_y| + \sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y| \,\le\, q^d|Y| + \sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y|, \end{align*} $$
$$ \begin{align*}|E|=\sum_{y \in Y} |E_y| + \sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y| \,\le\, q^d|Y| + \sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y|, \end{align*} $$
where the last inequality holds since
![]() $|E_y|\,\le \,q^d$
for
$|E_y|\,\le \,q^d$
for
![]() $y\in \mathbb {F}_q^d$
. Combining it with the assumption on
$y\in \mathbb {F}_q^d$
. Combining it with the assumption on
![]() $|E|$
gives the lower bound
$|E|$
gives the lower bound
 $$ \begin{align*} \displaystyle\sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y|\,\ge\, Cq^{d+{(d+1)}/{2}} - q^d|Y|. \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y|\,\ge\, Cq^{d+{(d+1)}/{2}} - q^d|Y|. \end{align*} $$
However, by definition,
![]() $|E_y|\,\le \,\tfrac 12C q^{{(d+1)}/{2}}$
for
$|E_y|\,\le \,\tfrac 12C q^{{(d+1)}/{2}}$
for
![]() $y \in \mathbb {F}^d_q\setminus Y$
, yielding the upper bound
$y \in \mathbb {F}^d_q\setminus Y$
, yielding the upper bound
 $$ \begin{align*} \displaystyle\sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y|\,\le\,\dfrac{1}{2}Cq^{d+{(d+1)}/{2}} .\end{align*} $$
$$ \begin{align*} \displaystyle\sum_{y \in \mathbb{F}^d_q\setminus Y} |E_y|\,\le\,\dfrac{1}{2}Cq^{d+{(d+1)}/{2}} .\end{align*} $$
These two bounds together give
![]() $Cq^{d+{(d+1)}/{2}} - q^d|Y|\,\le \,\tfrac 12C q^{d+{(d+1)}/{2}}$
, proving the claimed bound
$Cq^{d+{(d+1)}/{2}} - q^d|Y|\,\le \,\tfrac 12C q^{d+{(d+1)}/{2}}$
, proving the claimed bound
![]() $|Y|\,\ge \, \tfrac 12C q^{{(d+1)}/{2}}$
.
$|Y|\,\ge \, \tfrac 12C q^{{(d+1)}/{2}}$
.
In particular, Lemma 2.1 implies
![]() $|\Delta ^s(Y,Y)|\gg q$
, as
$|\Delta ^s(Y,Y)|\gg q$
, as
![]() $|Y||Y| \gg q^{d+1}$
. However, for each
$|Y||Y| \gg q^{d+1}$
. However, for each
![]() $u\in \Delta ^s(Y,Y)$
, there are
$u\in \Delta ^s(Y,Y)$
, there are
![]() $z, t\in Y$
such that
$z, t\in Y$
such that
![]() $\|z-t\|_s=u$
. One has
$\|z-t\|_s=u$
. One has
![]() $|E_z|, |E_t|\gg q^{{(d+1)}/{2}}$
, therefore, again by Lemma 2.1,
$|E_z|, |E_t|\gg q^{{(d+1)}/{2}}$
, therefore, again by Lemma 2.1,
![]() $|\Delta ^s(E_z, E_t)|\gg q$
. Furthermore, for
$|\Delta ^s(E_z, E_t)|\gg q$
. Furthermore, for
![]() $v\in \Delta ^s(E_z, E_t)$
, there are
$v\in \Delta ^s(E_z, E_t)$
, there are
![]() $x\in E_z$
and
$x\in E_z$
and
![]() $y\in E_t$
satisfying
$y\in E_t$
satisfying
![]() $\|x-y\|_s=v$
. Note that
$\|x-y\|_s=v$
. Note that
![]() $x\in E_z$
and
$x\in E_z$
and
![]() $y\in E_t$
mean that
$y\in E_t$
mean that
![]() $(x,z), (y,t)\in E$
. Thus,
$(x,z), (y,t)\in E$
. Thus,
![]() $(v,u)=(\|x-y\|_s, \|z-t\|_s)\in \Delta _{d, d}^s(E)$
. From this, we conclude that
$(v,u)=(\|x-y\|_s, \|z-t\|_s)\in \Delta _{d, d}^s(E)$
. From this, we conclude that
![]() $|\Delta _{d, d}^s(E)|\gg q|\Delta ^s(Y,Y)|\gg q^2$
, which completes the proof.
$|\Delta _{d, d}^s(E)|\gg q|\Delta ^s(Y,Y)|\gg q^2$
, which completes the proof.
3 Proof of Theorem 1.4
To improve the exponent over prime fields
![]() $\mathbb {F}_p$
, we strengthen Lemma 2.1 as shown in Lemma 3.1 below. Following the proof of Theorem 1.3 and using Lemma 3.1 proves Theorem 1.4.
$\mathbb {F}_p$
, we strengthen Lemma 2.1 as shown in Lemma 3.1 below. Following the proof of Theorem 1.3 and using Lemma 3.1 proves Theorem 1.4.
Lemma 3.1. Let
![]() $X, Y \subseteq \mathbb {F}_p^2$
. If
$X, Y \subseteq \mathbb {F}_p^2$
. If
![]() $|X|, |Y|\gg p^{5/4}$
, then
$|X|, |Y|\gg p^{5/4}$
, then
![]() $|\Delta (X, Y)|\gg p$
.
$|\Delta (X, Y)|\gg p$
.
Proof. It is clear that if
![]() $X' \subseteq X$
and
$X' \subseteq X$
and
![]() $Y' \subseteq Y$
, then
$Y' \subseteq Y$
, then
![]() $\Delta (X',Y')\subseteq \Delta (X,Y)$
. Thus, without loss of generality, we may assume that
$\Delta (X',Y')\subseteq \Delta (X,Y)$
. Thus, without loss of generality, we may assume that
![]() $|X|=|Y|=N$
with
$|X|=|Y|=N$
with
![]() $N\gg p^{5/ 4}$
. Let Q be the number of quadruples
$N\gg p^{5/ 4}$
. Let Q be the number of quadruples
![]() $(x, y, x', y')\in X\times Y\times X\times Y$
such that
$(x, y, x', y')\in X\times Y\times X\times Y$
such that
![]() $\|x-y\|=\|x'-y'\|$
. It follows easily from the Cauchy–Schwarz inequality that
$\|x-y\|=\|x'-y'\|$
. It follows easily from the Cauchy–Schwarz inequality that
 $$ \begin{align*}|\Delta(X, Y)|\gg \frac{|X|^2|Y|^2}{Q}.\end{align*} $$
$$ \begin{align*}|\Delta(X, Y)|\gg \frac{|X|^2|Y|^2}{Q}.\end{align*} $$
Let T be the number of triples
![]() $(x, y, y')\in X\times Y\times Y $
such that
$(x, y, y')\in X\times Y\times Y $
such that
![]() $\|x-y\|=\|x-y'\|$
. By the Cauchy–Schwarz inequality again, one gets
$\|x-y\|=\|x-y'\|$
. By the Cauchy–Schwarz inequality again, one gets
![]() $Q\ll |X|\cdot T$
. Next, we need to bound T. For this, denote
$Q\ll |X|\cdot T$
. Next, we need to bound T. For this, denote
![]() $Z=X\cup Y$
, so that
$Z=X\cup Y$
, so that
![]() $N\le |Z|\le 2N$
. Let
$N\le |Z|\le 2N$
. Let
![]() $T'$
be the number of triples
$T'$
be the number of triples
![]() $(a, b, c)\in Z\times Z\times Z$
such that
$(a, b, c)\in Z\times Z\times Z$
such that
![]() $\|a-b\|=\|a-c\|$
. Obviously,
$\|a-b\|=\|a-c\|$
. Obviously,
![]() $T\le T'$
. However, it was recently proved (see [Reference Murphy, Petridis, Pham, Rudnev and Stevens12, Theorem 4]) that
$T\le T'$
. However, it was recently proved (see [Reference Murphy, Petridis, Pham, Rudnev and Stevens12, Theorem 4]) that
 $$ \begin{align*}T'\ll \frac{|Z|^3}{p}+p^{2 /3}|Z|^{ 5 /3}+p^{1 /4}|Z|^2,\end{align*} $$
$$ \begin{align*}T'\ll \frac{|Z|^3}{p}+p^{2 /3}|Z|^{ 5 /3}+p^{1 /4}|Z|^2,\end{align*} $$
which gives
 $$ \begin{align*}T\ll \frac{N^3}{p}+p^{2 /3}N^{5 /3}+p^{1 /4}N^2,\end{align*} $$
$$ \begin{align*}T\ll \frac{N^3}{p}+p^{2 /3}N^{5 /3}+p^{1 /4}N^2,\end{align*} $$
and then
![]() $T\ll {N^3}/p$
(since
$T\ll {N^3}/p$
(since
![]() $N\gg p^{5 /4}$
). Putting all the bounds together, we obtain
$N\gg p^{5 /4}$
). Putting all the bounds together, we obtain
 $$ \begin{align*}\dfrac{N^3}{|\Delta(X,Y)|}=\dfrac{|X||Y|^2}{|\Delta(X,Y)|}\ll \dfrac Q{|X|}\ll T\ll \dfrac {N^3}p,\end{align*} $$
$$ \begin{align*}\dfrac{N^3}{|\Delta(X,Y)|}=\dfrac{|X||Y|^2}{|\Delta(X,Y)|}\ll \dfrac Q{|X|}\ll T\ll \dfrac {N^3}p,\end{align*} $$
or equivalently,
![]() $|\Delta (X,Y)|\gg p$
, as required.
$|\Delta (X,Y)|\gg p$
, as required.
Acknowledgement
The authors are grateful to Dr. Thang Pham for sharing insights and new ideas.