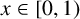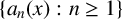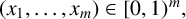1 Introduction
Let
![]() $T:[0,1)\to [0,1)$
be the Gauss map defined by
$T:[0,1)\to [0,1)$
be the Gauss map defined by
Every irrational number
![]() $x\in [0,1)$
can be uniquely expanded into an infinite form
$x\in [0,1)$
can be uniquely expanded into an infinite form
 $$ \begin{align} x:=\frac{1}{a_{1}(x)+\dfrac{1}{a_{2}(x)+\dfrac{1}{\ddots+\dfrac{1}{a_{n}+T^{n}(x)}}}} =\frac{1}{a_{1}(x)+\dfrac{1}{a_{2}(x)+\dfrac{1}{a_{3}(x)+\dfrac{1}{\ddots}}}}, \end{align} $$
$$ \begin{align} x:=\frac{1}{a_{1}(x)+\dfrac{1}{a_{2}(x)+\dfrac{1}{\ddots+\dfrac{1}{a_{n}+T^{n}(x)}}}} =\frac{1}{a_{1}(x)+\dfrac{1}{a_{2}(x)+\dfrac{1}{a_{3}(x)+\dfrac{1}{\ddots}}}}, \end{align} $$
where
![]() $a_{n}(x)=\lfloor 1/T^{n-1}(x)\rfloor $
are called the partial quotients of
$a_{n}(x)=\lfloor 1/T^{n-1}(x)\rfloor $
are called the partial quotients of
![]() $x.$
(Here
$x.$
(Here
![]() $\lfloor \cdot \rfloor $
denotes the greatest integer less than or equal to a real number and
$\lfloor \cdot \rfloor $
denotes the greatest integer less than or equal to a real number and
![]() $T^0$
denotes the identity map.) For simplicity of notation, we write (1.1) as
$T^0$
denotes the identity map.) For simplicity of notation, we write (1.1) as
It is clear that the Gauss transformation T acts as the shift map on the continued fraction system. That is, for each
![]() $x=[a_1(x),a_2(x),a_3(x),\ldots ]\in [0,1)\cap \mathbb {Q}^{c},$
$x=[a_1(x),a_2(x),a_3(x),\ldots ]\in [0,1)\cap \mathbb {Q}^{c},$
Gauss observed that T is measure-preserving and ergodic with respect to the Gauss measure
![]() $\mu $
defined by
$\mu $
defined by
 $$ \begin{align*}d\mu=\frac{1}{\log 2}\frac{1}{x+1}dx.\end{align*} $$
$$ \begin{align*}d\mu=\frac{1}{\log 2}\frac{1}{x+1}dx.\end{align*} $$
For more information on the continued fraction expansion, see [Reference Khintchine3].
The metrical theory of continued fractions, which concerns the properties of the partial quotients for almost all
![]() $x\in [0,1),$
is one of the major themes in the study of continued fractions. Wang and Wu [Reference Wang and Wu7] considered the metrical properties of the maximal run-length function
$x\in [0,1),$
is one of the major themes in the study of continued fractions. Wang and Wu [Reference Wang and Wu7] considered the metrical properties of the maximal run-length function
which counts the longest run of the same symbol among the first n partial quotients of x. They proved that, for
![]() $\mu $
almost all
$\mu $
almost all
![]() $x\in [0,1),$
$x\in [0,1),$
 $$ \begin{align*}\lim_{n\rightarrow\infty}\frac{R_{n}(x)}{\log n}=\frac{1}{2\log({(\sqrt{5}+1)}/{2})}.\end{align*} $$
$$ \begin{align*}\lim_{n\rightarrow\infty}\frac{R_{n}(x)}{\log n}=\frac{1}{2\log({(\sqrt{5}+1)}/{2})}.\end{align*} $$
Song and Zhou [Reference Song and Zhou6] gave a more subtle characterisation of the function
![]() $R_{n}(x).$
In this paper, we continue the study by considering the shortest distance function
$R_{n}(x).$
In this paper, we continue the study by considering the shortest distance function
 $$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1}) = & \cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k, \\&\ \text{and some}\ i \mbox{ with } 0\leq i \leq n-k\}. \end{align*} $$
$$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1}) = & \cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k, \\&\ \text{and some}\ i \mbox{ with } 0\leq i \leq n-k\}. \end{align*} $$
This is motivated by the behaviour of the shortest distance between two orbits,
in the continued fraction system. Shi et al. [Reference Shi, Tan and Zhou5] proved that, for
![]() $\mu ^{2}$
almost all
$\mu ^{2}$
almost all
![]() $(x,y)\in [0,1)\times [0,1),$
$(x,y)\in [0,1)\times [0,1),$
 $$ \begin{align*}{H_{2}}\cdot\lim_{n\rightarrow\infty}\frac{M_{n,2}(x,y)}{\log n}=\lim_{n\rightarrow\infty}\frac{-\log S_{n,2}(x,y)}{\log n},\end{align*} $$
$$ \begin{align*}{H_{2}}\cdot\lim_{n\rightarrow\infty}\frac{M_{n,2}(x,y)}{\log n}=\lim_{n\rightarrow\infty}\frac{-\log S_{n,2}(x,y)}{\log n},\end{align*} $$
where
![]() $H_{2}$
is the Rényi entropy defined by (1.2). Investigating the shortest distance between two orbits amounts to estimating the longest common substrings between two sequences of partial quotients. In fact, [Reference Shi, Tan and Zhou5] focused on the asymptotics of the length of the longest common substrings in two sequences of partial quotients.
$H_{2}$
is the Rényi entropy defined by (1.2). Investigating the shortest distance between two orbits amounts to estimating the longest common substrings between two sequences of partial quotients. In fact, [Reference Shi, Tan and Zhou5] focused on the asymptotics of the length of the longest common substrings in two sequences of partial quotients.
For
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $(a_{1},\ldots ,a_{n})\in \mathbb {N}^{n}$
, we call
$(a_{1},\ldots ,a_{n})\in \mathbb {N}^{n}$
, we call
an nth cylinder. For
![]() $m\geq 2$
, we define the generalised Rényi entropy with respect to the Gauss measure
$m\geq 2$
, we define the generalised Rényi entropy with respect to the Gauss measure
![]() $\mu $
by
$\mu $
by
 $$ \begin{align} {H}_{m}=\lim_{n\rightarrow\infty}\frac{-\log \sum_{(a_1,\ldots,a_n)\in \mathbb{N}^{n}} \mu(I_{n}(a_1,\ldots,a_n))^{m}}{(m-1)n}. \end{align} $$
$$ \begin{align} {H}_{m}=\lim_{n\rightarrow\infty}\frac{-\log \sum_{(a_1,\ldots,a_n)\in \mathbb{N}^{n}} \mu(I_{n}(a_1,\ldots,a_n))^{m}}{(m-1)n}. \end{align} $$
The existence of the limit (1.2) for the Gauss measure
![]() $\mu $
was established in [Reference Haydn and Vaienti2].
$\mu $
was established in [Reference Haydn and Vaienti2].
Theorem 1.1. For
![]() $\mu ^{m}$
-almost all
$\mu ^{m}$
-almost all
![]() $(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
 $$ \begin{align*}\lim_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\frac{1}{(m-1)H_{m}}.\end{align*} $$
$$ \begin{align*}\lim_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\frac{1}{(m-1)H_{m}}.\end{align*} $$
Here we use the convention that
![]() ${1}/{0}=\infty $
and
${1}/{0}=\infty $
and
![]() ${1}/{\infty }=0.$
${1}/{\infty }=0.$
It is natural to study the exceptional set in this limit theorem. We define the exceptional set as
 $$ \begin{align*}\widetilde{E}=\bigg\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: \liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n} <\limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\bigg\}\end{align*} $$
$$ \begin{align*}\widetilde{E}=\bigg\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: \liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n} <\limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\bigg\}\end{align*} $$
and the level set as
 $$ \begin{align*}E(\alpha)=\bigg\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: \lim_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\alpha\bigg\}.\end{align*} $$
$$ \begin{align*}E(\alpha)=\bigg\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: \lim_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\alpha\bigg\}.\end{align*} $$
Throughout the paper,
![]() $\dim _{H}A$
denotes the Hausdorff dimension of the set
$\dim _{H}A$
denotes the Hausdorff dimension of the set
![]() $A.$
$A.$
Theorem 1.2. For any
![]() $\alpha $
with
$\alpha $
with
![]() $0\leq \alpha \leq \infty ,$
$0\leq \alpha \leq \infty ,$
![]() $\dim _{H}\widetilde {E}=\dim _{H}E(\alpha )=m.$
$\dim _{H}\widetilde {E}=\dim _{H}E(\alpha )=m.$
In fact, Theorem 1.2 follows immediately from the following more general result. For any
![]() $0\leq \alpha \leq \beta \leq \infty ,$
set
$0\leq \alpha \leq \beta \leq \infty ,$
set
 $$ \begin{align*} E(\alpha,\beta)=\bigg\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: & \liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\alpha, \\ & \limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\beta\bigg\}. \end{align*} $$
$$ \begin{align*} E(\alpha,\beta)=\bigg\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: & \liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\alpha, \\ & \limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}=\beta\bigg\}. \end{align*} $$
Theorem 1.3. For any
![]() $\alpha ,\beta $
with
$\alpha ,\beta $
with
![]() $0\leq \alpha \leq \beta \leq \infty ,$
$0\leq \alpha \leq \beta \leq \infty ,$
![]() $\dim _{H}E(\alpha ,\beta )=m.$
$\dim _{H}E(\alpha ,\beta )=m.$
2 Preliminaries
In this section, we fix some notation and recall some basic properties of continued fraction expansions. A detailed account of continued fractions can be found in Khintchine’s book [Reference Khintchine3].
For any irrational number
![]() $x\in [0,1)$
with continued fraction expansion (1.1), we denote by
$x\in [0,1)$
with continued fraction expansion (1.1), we denote by
 $$ \begin{align*}\frac{p_{n}(x)}{ q_{n}(x)} :=[a_{1}(x),\ldots,a_{n}(x)]\end{align*} $$
$$ \begin{align*}\frac{p_{n}(x)}{ q_{n}(x)} :=[a_{1}(x),\ldots,a_{n}(x)]\end{align*} $$
the nth convergent of
![]() $x.$
With the conventions
$x.$
With the conventions
we have, for any
![]() $n\ge 0,$
$n\ge 0,$
Obviously,
![]() $q_{n}(x)$
is determined by the first n partial quotients
$q_{n}(x)$
is determined by the first n partial quotients
![]() $a_{1}(x),\ldots ,a_{n}(x).$
So we also write
$a_{1}(x),\ldots ,a_{n}(x).$
So we also write
![]() $q_{n}(a_{1}(x),\ldots ,a_{n}(x))$
in place of
$q_{n}(a_{1}(x),\ldots ,a_{n}(x))$
in place of
![]() $q_{n}(x).$
If no confusion is likely to arise, we write
$q_{n}(x).$
If no confusion is likely to arise, we write
![]() $a_{n}$
and
$a_{n}$
and
![]() $q_{n}$
in place of
$q_{n}$
in place of
![]() $a_{n}(x)$
and
$a_{n}(x)$
and
![]() $q_{n}(x),$
respectively.
$q_{n}(x),$
respectively.
Proposition 2.1 [Reference Khintchine3].
For
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $(a_{1},\ldots ,a_{n})\in \mathbb {N}^{n}$
:
$(a_{1},\ldots ,a_{n})\in \mathbb {N}^{n}$
:
-
(1)
 $ q_n\ge 2^{(n-1)/2}$
and
$ q_n\ge 2^{(n-1)/2}$
and  $$ \begin{align*} \prod^{n}_{k=1}a_{k}\leq q_n \leq \prod^{n}_{k=1}(a_{k}+1)\leq 2^{n}\prod^{n}_{k=1}a_{k};\end{align*} $$
$$ \begin{align*} \prod^{n}_{k=1}a_{k}\leq q_n \leq \prod^{n}_{k=1}(a_{k}+1)\leq 2^{n}\prod^{n}_{k=1}a_{k};\end{align*} $$
-
(2) the length of
 $I_{n}(a_{1},\ldots ,a_{n})$
satisfies
$I_{n}(a_{1},\ldots ,a_{n})$
satisfies  $$ \begin{align*} \frac{1}{2q_n^2} \leq |I_{n}(a_{1},\ldots,a_{n})|=\frac{1}{(q_n+q_{n-1})q_n} \leq \frac{1}{q_n^2}. \end{align*} $$
$$ \begin{align*} \frac{1}{2q_n^2} \leq |I_{n}(a_{1},\ldots,a_{n})|=\frac{1}{(q_n+q_{n-1})q_n} \leq \frac{1}{q_n^2}. \end{align*} $$
The following
![]() $\psi $
-mixing property is essential in proving Theorem 1.1.
$\psi $
-mixing property is essential in proving Theorem 1.1.
Lemma 2.2 [Reference Philipp4].
For any
![]() $k\geq 1,$
let
$k\geq 1,$
let
![]() $\mathbb {B}^{k}_{1}=\sigma (a_{1},\ldots ,a_{k})$
and let
$\mathbb {B}^{k}_{1}=\sigma (a_{1},\ldots ,a_{k})$
and let
![]() $\mathbb {B}^{\infty }_{k}=\sigma (a_{k},a_{k+1},\ldots )$
denote the
$\mathbb {B}^{\infty }_{k}=\sigma (a_{k},a_{k+1},\ldots )$
denote the
![]() $\sigma $
-algebras generated by the random variables
$\sigma $
-algebras generated by the random variables
![]() $(a_{1},\ldots ,a_{k})$
and
$(a_{1},\ldots ,a_{k})$
and
![]() $(a_{k},a_{k+1},\ldots )$
respectively. Then, for any
$(a_{k},a_{k+1},\ldots )$
respectively. Then, for any
![]() $E\in \mathbb {B}^{k}_{1}$
and
$E\in \mathbb {B}^{k}_{1}$
and
![]() $F\in \mathbb {B}^{\infty }_{k+n},$
$F\in \mathbb {B}^{\infty }_{k+n},$
where
![]() $|\theta |\leq K, \rho <1$
and
$|\theta |\leq K, \rho <1$
and
![]() $K, \rho $
are positive constants independent of
$K, \rho $
are positive constants independent of
![]() $E, F, n$
and
$E, F, n$
and
![]() $k.$
$k.$
To estimate the measure of a limsup set in a probability space, the following lemma is widely used.
Lemma 2.3 (Borel–Cantelli lemma).
Let
![]() $(\Omega , \mathcal {B}, \nu )$
be a finite measure space and let
$(\Omega , \mathcal {B}, \nu )$
be a finite measure space and let
![]() $\{A_n\}_{n\ge 1}$
be a sequence of measurable sets. Define
$\{A_n\}_{n\ge 1}$
be a sequence of measurable sets. Define
![]() $A=\bigcap _{N=1}^{\infty }\bigcup _{n=N}^{\infty }A_n.$
Then
$A=\bigcap _{N=1}^{\infty }\bigcup _{n=N}^{\infty }A_n.$
Then
 $$ \begin{align*} \nu(A)=\begin{cases} 0 & \text{if } \displaystyle\sum_{n= 1}^{\infty}\nu(A_n)<\infty, \\[3pt] \nu(\Omega) & \displaystyle \text{if }\sum_{n= 1}^{\infty}\nu(A_n)=\infty \text{ and } \{A_n\}_{n\ge 1}\text{ are pairwise independent}. \end{cases} \end{align*} $$
$$ \begin{align*} \nu(A)=\begin{cases} 0 & \text{if } \displaystyle\sum_{n= 1}^{\infty}\nu(A_n)<\infty, \\[3pt] \nu(\Omega) & \displaystyle \text{if }\sum_{n= 1}^{\infty}\nu(A_n)=\infty \text{ and } \{A_n\}_{n\ge 1}\text{ are pairwise independent}. \end{cases} \end{align*} $$
Let
![]() $\mathbb {K}=\{k_{n}\}_{n\geq 1}$
be a subsequence of
$\mathbb {K}=\{k_{n}\}_{n\geq 1}$
be a subsequence of
![]() $\mathbb {N}$
that is not cofinite. Define a mapping
$\mathbb {N}$
that is not cofinite. Define a mapping
![]() $\phi _{\mathbb {K}}:[0,1)\cap \mathbb {Q}^{c}\rightarrow [0,1)\cap \mathbb {Q}^{c}$
as follows. For each
$\phi _{\mathbb {K}}:[0,1)\cap \mathbb {Q}^{c}\rightarrow [0,1)\cap \mathbb {Q}^{c}$
as follows. For each
![]() $x=[a_1,a_2,\ldots ]\in [0,1)\cap \mathbb {Q}^{c},$
put
$x=[a_1,a_2,\ldots ]\in [0,1)\cap \mathbb {Q}^{c},$
put
![]() $\phi _{\mathbb {K}}(x)=\overline {x}=[c_1,c_2,\ldots ],$
where
$\phi _{\mathbb {K}}(x)=\overline {x}=[c_1,c_2,\ldots ],$
where
![]() $[c_1,c_2,\ldots ]$
is obtained by eliminating all the terms
$[c_1,c_2,\ldots ]$
is obtained by eliminating all the terms
![]() $a_{k_{n}}$
from the sequence
$a_{k_{n}}$
from the sequence
![]() $a_1, a_2,\ldots .$
Let
$a_1, a_2,\ldots .$
Let
![]() $\{b_{n}\}_{n\geq 1}$
be a sequence with
$\{b_{n}\}_{n\geq 1}$
be a sequence with
![]() $b_{n}\in \mathbb {N},n\geq 1.$
Write
$b_{n}\in \mathbb {N},n\geq 1.$
Write
Lemma 2.4 [Reference Song and Zhou6].
Assume that
![]() $\{b_{n}\}_{n\geq 1}$
is bounded. If the sequence
$\{b_{n}\}_{n\geq 1}$
is bounded. If the sequence
![]() $\mathbb {K}$
is of density zero in
$\mathbb {K}$
is of density zero in
![]() $\mathbb {N},$
that is,
$\mathbb {N},$
that is,
where
![]() $\sharp $
denotes the number of elements in a set, then
$\sharp $
denotes the number of elements in a set, then
We close this section by citing Marstrand’s product theorem.
Lemma 2.5 [Reference Falconer1].
If
![]() $E,F\subset \mathbb {R}^{d}$
for some
$E,F\subset \mathbb {R}^{d}$
for some
![]() $d,$
then
$d,$
then
![]() $\dim _{H}(E\times F)\geq \dim _{H}E+\dim _{H}F.$
$\dim _{H}(E\times F)\geq \dim _{H}E+\dim _{H}F.$
3 Proof of Theorem 1.1
Theorem 1.1 can be proved from the following two propositions.
Proposition 3.1. For
![]() $\mu ^{m}$
-almost all
$\mu ^{m}$
-almost all
![]() $(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
 $$ \begin{align*}\limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\leq\frac{1}{(m-1)H_{m}}.\end{align*} $$
$$ \begin{align*}\limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\leq\frac{1}{(m-1)H_{m}}.\end{align*} $$
Proof. We can assume that
![]() $H_{m}>0$
(the case
$H_{m}>0$
(the case
![]() $H_m=0$
is obvious). Fix
$H_m=0$
is obvious). Fix
![]() $s_1< s_2< (m-1)H_{m}.$
By the definition of the
$s_1< s_2< (m-1)H_{m}.$
By the definition of the
![]() $H_{m},$
$H_{m},$
 $$ \begin{align} \sum_{(a_{1},\ldots,a_{n})\in\mathbb{N}^{n}}\mu(I_{n}(a_{1},\ldots,a_{n}))^{m}<\exp\bigg\{-\frac{s_1+s_2}{2}n\bigg\} \end{align} $$
$$ \begin{align} \sum_{(a_{1},\ldots,a_{n})\in\mathbb{N}^{n}}\mu(I_{n}(a_{1},\ldots,a_{n}))^{m}<\exp\bigg\{-\frac{s_1+s_2}{2}n\bigg\} \end{align} $$
for sufficiently large n. Set
![]() $u_{n}=\lfloor {\log n}/{s_1}\rfloor .$
Note that, for any
$u_{n}=\lfloor {\log n}/{s_1}\rfloor .$
Note that, for any
![]() $(x_{1},\ldots ,x_{m})\in [0,1)^{m}$
with
$(x_{1},\ldots ,x_{m})\in [0,1)^{m}$
with
![]() $M_{n,m}(x_{1},\ldots ,x_{m})=k$
, there exists i with
$M_{n,m}(x_{1},\ldots ,x_{m})=k$
, there exists i with
![]() $0\leq i\leq n-k$
such that
$0\leq i\leq n-k$
such that
for
![]() $j=1,\ldots ,k.$
We deduce
$j=1,\ldots ,k.$
We deduce
 $$ \begin{align*} &\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots,x_{m})>u_{n}\})\\ &\quad =\sum_{k=u_{n}+1}^{\infty}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots,x_{m})=k\})\\ &\quad \leq\sum_{k=u_{n}+1}^{\infty}\sum_{i=0}^{n-k}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: a_{i+j}(x_{1})=\cdots=a_{i+j}(x_{m}),\ j=1,\ldots,k\}). \end{align*} $$
$$ \begin{align*} &\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots,x_{m})>u_{n}\})\\ &\quad =\sum_{k=u_{n}+1}^{\infty}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots,x_{m})=k\})\\ &\quad \leq\sum_{k=u_{n}+1}^{\infty}\sum_{i=0}^{n-k}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: a_{i+j}(x_{1})=\cdots=a_{i+j}(x_{m}),\ j=1,\ldots,k\}). \end{align*} $$
By the invariance of
![]() $\mu $
under
$\mu $
under
![]() $T,$
it follows that
$T,$
it follows that
 $$ \begin{align*} &\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots,x_{m})>u_{n}\})\\&\quad\leq n \sum_{k=u_{n}+1}^{\infty}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: a_{j}(x_{1})=\cdots=a_{j}(x_{m}),\ j=1,\ldots,k\})\\&\quad= n\sum_{k=u_{n}+1}^{\infty}\sum_{(a_{1},\ldots,a_{k})\in \mathbb{N}^{k}}\mu(I_{k}(a_{1},\ldots,a_{k}))^{m}\\&\quad\leq Cn\cdot\exp\bigg\{-\frac{s_1+s_2}{2}(u_{n}+1)\bigg\} \qquad (\text{by } (3.1))\\&\quad\leq Cn^{-{(s_2-s_1)}/{2s_1}}, \end{align*} $$
$$ \begin{align*} &\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots,x_{m})>u_{n}\})\\&\quad\leq n \sum_{k=u_{n}+1}^{\infty}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: a_{j}(x_{1})=\cdots=a_{j}(x_{m}),\ j=1,\ldots,k\})\\&\quad= n\sum_{k=u_{n}+1}^{\infty}\sum_{(a_{1},\ldots,a_{k})\in \mathbb{N}^{k}}\mu(I_{k}(a_{1},\ldots,a_{k}))^{m}\\&\quad\leq Cn\cdot\exp\bigg\{-\frac{s_1+s_2}{2}(u_{n}+1)\bigg\} \qquad (\text{by } (3.1))\\&\quad\leq Cn^{-{(s_2-s_1)}/{2s_1}}, \end{align*} $$
where
![]() $C=\sum _{k=1}^{\infty }\exp \{-{(s_1+s_2)k}/{2}\}.$
Choose an infinite subsequence of integers
$C=\sum _{k=1}^{\infty }\exp \{-{(s_1+s_2)k}/{2}\}.$
Choose an infinite subsequence of integers
![]() $\{n_{k}\}_{k\geq 1},$
where
$\{n_{k}\}_{k\geq 1},$
where
![]() $n_{k}=k^{L}$
and
$n_{k}=k^{L}$
and
![]() $L\cdot {(s_2-s_1)}/{2s_1}>1.$
Then
$L\cdot {(s_2-s_1)}/{2s_1}>1.$
Then
 $$ \begin{align*} \sum_{k=1}^{\infty}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n_{k},m}(x_{1},\ldots,x_{m})>u_{n_{k}}\})<\infty. \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\infty}\mu^{m}(\{(x_{1},\ldots,x_{m})\in [0,1)^{m}: M_{n_{k},m}(x_{1},\ldots,x_{m})>u_{n_{k}}\})<\infty. \end{align*} $$
From the Borel–Cantelli Lemma 2.3, for almost all
![]() $(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
for sufficiently large k. Thus,
 $$ \begin{align*} \limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n} \leq&\limsup_{k\rightarrow\infty}\frac{M_{n_{k+1},m}(x_{1},\ldots,x_{m})}{\log n_{k}}\\ \leq&\limsup_{k\rightarrow\infty}\frac{M_{n_{k+1},m}(x_{1},\ldots,x_{m})}{\log n_{k+1}}\cdot\limsup_{k\rightarrow\infty}\frac{n_{k+1}}{n_{k}} \leq\frac{1}{s_{1}}. \end{align*} $$
$$ \begin{align*} \limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n} \leq&\limsup_{k\rightarrow\infty}\frac{M_{n_{k+1},m}(x_{1},\ldots,x_{m})}{\log n_{k}}\\ \leq&\limsup_{k\rightarrow\infty}\frac{M_{n_{k+1},m}(x_{1},\ldots,x_{m})}{\log n_{k+1}}\cdot\limsup_{k\rightarrow\infty}\frac{n_{k+1}}{n_{k}} \leq\frac{1}{s_{1}}. \end{align*} $$
Therefore, by the arbitrariness of
![]() $s_{1},$
$s_{1},$
 $$ \begin{align*}\limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\leq\frac{1}{(m-1)H_{m}}.\end{align*} $$
$$ \begin{align*}\limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\leq\frac{1}{(m-1)H_{m}}.\end{align*} $$
This completes the proof.
Proposition 3.2. For
![]() $\mu ^{m}$
-almost all
$\mu ^{m}$
-almost all
![]() $(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
 $$ \begin{align*}\liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\geq\frac{1}{(m-1)H_{m}}.\end{align*} $$
$$ \begin{align*}\liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\geq\frac{1}{(m-1)H_{m}}.\end{align*} $$
Proof. We can assume that
![]() $H_{m}<\infty $
(the case
$H_{m}<\infty $
(the case
![]() $H_m=\infty $
is obvious). For
$H_m=\infty $
is obvious). For
![]() $1\le d<n$
, set
$1\le d<n$
, set
 $$ \begin{align*} M_{[d,n]}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1}) & =\cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k, \\&\ \text{and for some } i \mbox{ with } d-1\leq i \leq n-k\}. \end{align*} $$
$$ \begin{align*} M_{[d,n]}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1}) & =\cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k, \\&\ \text{and for some } i \mbox{ with } d-1\leq i \leq n-k\}. \end{align*} $$
We denote
![]() $\{(x_{1},\ldots ,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots ,x_{m})<k\}$
by
$\{(x_{1},\ldots ,x_{m})\in [0,1)^{m}: M_{n,m}(x_{1},\ldots ,x_{m})<k\}$
by
![]() $\{M_{n,m}<k\}$
for brevity.
$\{M_{n,m}<k\}$
for brevity.
For any
![]() $s>(m-1)H_{m},$
by the definition of the
$s>(m-1)H_{m},$
by the definition of the
![]() $H_{m},$
$H_{m},$
 $$ \begin{align} \sum_{(a_{1},\ldots,a_{n}) \in\mathbb{N}^{n}}\mu(I_{n}(a_{1},\ldots,a_{n}))^{m}>\exp\bigg\{-\frac{s+(m-1)H_{m}}{2}n\bigg\} \end{align} $$
$$ \begin{align} \sum_{(a_{1},\ldots,a_{n}) \in\mathbb{N}^{n}}\mu(I_{n}(a_{1},\ldots,a_{n}))^{m}>\exp\bigg\{-\frac{s+(m-1)H_{m}}{2}n\bigg\} \end{align} $$
for sufficiently large n. Let
![]() $u_{n}=\lfloor {\log n}/{s}\rfloor $
and
$u_{n}=\lfloor {\log n}/{s}\rfloor $
and
![]() $l_{n}=\lfloor {n}/{u_{n}^{2}}\rfloor .$
Then
$l_{n}=\lfloor {n}/{u_{n}^{2}}\rfloor .$
Then
 $$ \begin{align*} \begin{aligned} \{M_{n,m}<u_{n}\}&\subset \{M_{[iu_{n}^{2}+1,iu_{n}^{2}+u_{n}]}<u_{n} : 0\leq i <l_{n}\}\\& \subset\{M_{u_{n},m}<u_{n}\}\cap(\underbrace{T\times\cdots \times T}_{m \text{ times }})^{-u_{n}^{2}}\{M_{[iu_{n}^{2}+1,i\mu_{n}^{2}+u_{n}]}<u_{n} : 0\leq i <l_{n}-1\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \{M_{n,m}<u_{n}\}&\subset \{M_{[iu_{n}^{2}+1,iu_{n}^{2}+u_{n}]}<u_{n} : 0\leq i <l_{n}\}\\& \subset\{M_{u_{n},m}<u_{n}\}\cap(\underbrace{T\times\cdots \times T}_{m \text{ times }})^{-u_{n}^{2}}\{M_{[iu_{n}^{2}+1,i\mu_{n}^{2}+u_{n}]}<u_{n} : 0\leq i <l_{n}-1\}. \end{aligned} \end{align*} $$
By Lemma 2.2, it follows that
 $$ \begin{align*} & \mu^{m}(\{M_{n,m}<u_{n}\}) \\& \quad \leq \mu^{m}(\{M_{u_{n},m}<u_{n}\}\cap(\underbrace{T\times\cdots \times T}_{m \text{ times }})^{-u_{n}^{2}}\{M_{[iu_{n}^{2}+1,i\mu_{n}^{2}+u_{n}]}<u_{n}, 0\leq i <l_{n}-1\})\\& \quad \leq\mu^{m}(\{M_{u_{n},m}<u_{n}\})^{l_{n}}(1+\theta \rho^{u_{n}^{2}-u_{n}})^{m\cdot l_{n}}\\& \quad \leq\bigg(1-\sum_{(a_{1},\ldots,a_{u_{n}})\in \mathbb{N}^{u_{n}}} \mu(I_{u_{n}}(a_{1},\ldots,a_{u_{n}}))^{m}\bigg)^{l_{n}}(1+\theta \rho^{u_{n}^{2}-u_{n}})^{m\cdot l_{n}}\\& \quad \leq\exp\bigg\{-\frac{n}{u_{n}^{2}}\cdot n^{-{(s+(m-1)H_{m})}/{2s}}\bigg\}\cdot\exp\bigg\{\theta \rho^{u_{n}^{2}-u_{n}}\frac{m\cdot n}{u_{n}^{2}}\bigg\}\\& \quad \leq M\exp\bigg\{-\frac{n^{{(s-(m-1)H_{m})}/{2s}}}{u_{n}^{2}}\bigg\}, \end{align*} $$
$$ \begin{align*} & \mu^{m}(\{M_{n,m}<u_{n}\}) \\& \quad \leq \mu^{m}(\{M_{u_{n},m}<u_{n}\}\cap(\underbrace{T\times\cdots \times T}_{m \text{ times }})^{-u_{n}^{2}}\{M_{[iu_{n}^{2}+1,i\mu_{n}^{2}+u_{n}]}<u_{n}, 0\leq i <l_{n}-1\})\\& \quad \leq\mu^{m}(\{M_{u_{n},m}<u_{n}\})^{l_{n}}(1+\theta \rho^{u_{n}^{2}-u_{n}})^{m\cdot l_{n}}\\& \quad \leq\bigg(1-\sum_{(a_{1},\ldots,a_{u_{n}})\in \mathbb{N}^{u_{n}}} \mu(I_{u_{n}}(a_{1},\ldots,a_{u_{n}}))^{m}\bigg)^{l_{n}}(1+\theta \rho^{u_{n}^{2}-u_{n}})^{m\cdot l_{n}}\\& \quad \leq\exp\bigg\{-\frac{n}{u_{n}^{2}}\cdot n^{-{(s+(m-1)H_{m})}/{2s}}\bigg\}\cdot\exp\bigg\{\theta \rho^{u_{n}^{2}-u_{n}}\frac{m\cdot n}{u_{n}^{2}}\bigg\}\\& \quad \leq M\exp\bigg\{-\frac{n^{{(s-(m-1)H_{m})}/{2s}}}{u_{n}^{2}}\bigg\}, \end{align*} $$
where the penultimate inequality follows from (3.2) and the two facts
![]() $ (1-x)<\exp (-x)$
for
$ (1-x)<\exp (-x)$
for
![]() $0<x<1$
and
$0<x<1$
and
![]() $\lim _{n\to \infty }(1+1/n)^{n}=e$
, and the last inequality follows because
$\lim _{n\to \infty }(1+1/n)^{n}=e$
, and the last inequality follows because
![]() $\theta \rho ^{u_{n}^{2}-u_{n}}{m\cdot n}/{u_{n}^{2}}\rightarrow 0$
as
$\theta \rho ^{u_{n}^{2}-u_{n}}{m\cdot n}/{u_{n}^{2}}\rightarrow 0$
as
![]() $n\rightarrow \infty .$
Thus,
$n\rightarrow \infty .$
Thus,
 $$ \begin{align*} \sum_{n=1}^{\infty}\mu^{m}(\{M_{n,m}<u_{n}\})<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}\mu^{m}(\{M_{n,m}<u_{n}\})<\infty. \end{align*} $$
From the Borel–Cantelli Lemma, for
![]() $\mu ^{m}$
-almost all
$\mu ^{m}$
-almost all
![]() $(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$
 $$ \begin{align*}\liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\geq\frac{1}{(m-1)H_{m}}.\end{align*} $$
$$ \begin{align*}\liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}\geq\frac{1}{(m-1)H_{m}}.\end{align*} $$
This completes the proof of Proposition 3.2 and of Theorem 1.1.
4 Proof of Theorem 1.3
This section is devoted to the proof of Theorem 1.3. Our strategy is to construct Cantor-like subsets with full Hausdorff dimension. The proof is divided into several cases according to the values of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta .$
We give a detailed proof for the case
$\beta .$
We give a detailed proof for the case
![]() $0<\alpha <\beta <\infty $
and a sketch of the proof for the remaining cases.
$0<\alpha <\beta <\infty $
and a sketch of the proof for the remaining cases.
Case 1:
![]() $0<\alpha <\beta <\infty .$
$0<\alpha <\beta <\infty .$
Choose two positive integer sequences
![]() $\{n_{k}\}_{k\geq 1}$
and
$\{n_{k}\}_{k\geq 1}$
and
![]() $\{s_{k}\}_{k\geq 1}$
such that, for each
$\{s_{k}\}_{k\geq 1}$
such that, for each
![]() $k\geq 1,$
$k\geq 1,$
We readily check that
Without loss of generality, we assume that
![]() $n_{k+1}-n_{k}>s_{k}$
for all
$n_{k+1}-n_{k}>s_{k}$
for all
![]() $k\geq 1.$
Otherwise, we consider only sufficiently large k. Put
$k\geq 1.$
Otherwise, we consider only sufficiently large k. Put
where
Define a marked set
![]() $\mathbb {K}$
of positive integers by
$\mathbb {K}$
of positive integers by
Now we define m sequences as follows.
-
• For
 $i=1,$
$i=1,$
 $$ \begin{align*}a_{n_{k}}^{(1)}=1,\ a_{n_{k}+1}^{(1)}=\cdots=a_{n_{k}+s_{k}-1}^{(1)}=1,\ a_{n_{k}+s_{k}}^{(1)}=a_{n_{k}+2s_{k}}^{(1)}= \cdots=a_{n_{k}+\iota_ks_{k}}^{(1)}=1.\end{align*} $$
$$ \begin{align*}a_{n_{k}}^{(1)}=1,\ a_{n_{k}+1}^{(1)}=\cdots=a_{n_{k}+s_{k}-1}^{(1)}=1,\ a_{n_{k}+s_{k}}^{(1)}=a_{n_{k}+2s_{k}}^{(1)}= \cdots=a_{n_{k}+\iota_ks_{k}}^{(1)}=1.\end{align*} $$
-
• For
 $2\leq i\leq m,$
$2\leq i\leq m,$
 $$ \begin{align*}a_{n_{k}}^{(i)}=i,\ a_{n_{k}+1}^{(i)}=\cdots=a_{n_{k}+s_{k}-1}^{(i)}=1,\ a_{n_{k}+s_{k}}^{(i)}=a_{n_{k}+2s_{k}}^{(i)}= \cdots=a_{n_{k}+\iota_ks_{k}}^{(i)}=i.\end{align*} $$
$$ \begin{align*}a_{n_{k}}^{(i)}=i,\ a_{n_{k}+1}^{(i)}=\cdots=a_{n_{k}+s_{k}-1}^{(i)}=1,\ a_{n_{k}+s_{k}}^{(i)}=a_{n_{k}+2s_{k}}^{(i)}= \cdots=a_{n_{k}+\iota_ks_{k}}^{(i)}=i.\end{align*} $$
Then, for
![]() $i=1,2,\ldots ,m,$
write
$i=1,2,\ldots ,m,$
write
Now we prove
![]() $\prod _{i=1}^{m}E(\mathbb {K},\{a_{n}^{(i)}\}_{n\geq 1})\subset E(\alpha ,\beta ).$
Fix
$\prod _{i=1}^{m}E(\mathbb {K},\{a_{n}^{(i)}\}_{n\geq 1})\subset E(\alpha ,\beta ).$
Fix
![]() $(x_{1},\ldots ,x_{m})\in \prod _{i=1}^{m}E(\mathbb {K},\{a_{n}^{(i)}\}_{n\geq 1})$
for any
$(x_{1},\ldots ,x_{m})\in \prod _{i=1}^{m}E(\mathbb {K},\{a_{n}^{(i)}\}_{n\geq 1})$
for any
![]() $n\geq n_{1}$
and let k be the integer such that
$n\geq n_{1}$
and let k be the integer such that
![]() $n_{k}\leq n< n_{k+1}.$
From the construction of the set
$n_{k}\leq n< n_{k+1}.$
From the construction of the set
![]() $\prod _{i=1}^{m}E(\mathbb {K},\{a_{n}^{(i)}\}_{n\geq 1})$
, we see that
$\prod _{i=1}^{m}E(\mathbb {K},\{a_{n}^{(i)}\}_{n\geq 1})$
, we see that
 $$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\begin{cases} s_{k-1}-1 & \text{if}\ n_{k}\leq n<n_{k}+s_{k-1},\\ n-n_{k} & \text{if}\ n_{k}+s_{k-1}\leq n<n_{k}+s_{k},\\ s_{k}-1 & \text{if}\ n_{k}+s_{k}\leq n<n_{k+1}. \end{cases} \end{align*} $$
$$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\begin{cases} s_{k-1}-1 & \text{if}\ n_{k}\leq n<n_{k}+s_{k-1},\\ n-n_{k} & \text{if}\ n_{k}+s_{k-1}\leq n<n_{k}+s_{k},\\ s_{k}-1 & \text{if}\ n_{k}+s_{k}\leq n<n_{k+1}. \end{cases} \end{align*} $$
Further, by (4.1), we deduce that
 $$ \begin{align*} \begin{aligned} \liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}&= \liminf_{k\rightarrow\infty} \min\bigg\{\frac{M_{n_{k}+s_{k-1}-1,m}(x_{1},\ldots,x_{m})}{\log(n_{k}+s_{k-1}-1)},\frac{M_{n_{k+1}-1,m}(x_{1},\ldots,x_{m})}{\log(n_{k+1}-1)}\bigg\}\\& =\liminf_{k\rightarrow\infty} \min\bigg\{\frac{s_{k-1}-1}{\log(n_{k}+s_{k-1}-1)},\frac{s_{k}-1}{\log(n_{k+1}-1)}\bigg\}\\& =\alpha \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \liminf_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}&= \liminf_{k\rightarrow\infty} \min\bigg\{\frac{M_{n_{k}+s_{k-1}-1,m}(x_{1},\ldots,x_{m})}{\log(n_{k}+s_{k-1}-1)},\frac{M_{n_{k+1}-1,m}(x_{1},\ldots,x_{m})}{\log(n_{k+1}-1)}\bigg\}\\& =\liminf_{k\rightarrow\infty} \min\bigg\{\frac{s_{k-1}-1}{\log(n_{k}+s_{k-1}-1)},\frac{s_{k}-1}{\log(n_{k+1}-1)}\bigg\}\\& =\alpha \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}&= \limsup_{k\rightarrow\infty} \max\bigg\{\frac{M_{n_{k},m}(x_{1},\ldots,x_{m})}{\log(n_{k})},\frac{M_{n_{k}+s_{k}-1,m}(x_{1},\ldots,x_{m})}{\log(n_{k}+s_{k}-1)}\bigg\}\\& =\limsup_{k\rightarrow\infty} \max\bigg\{\frac{s_{k-1}-1}{\log(n_{k})},\frac{s_{k}-1}{\log(n_{k}+s_{k}-1)}\bigg\}\\& =\beta. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \limsup_{n\rightarrow\infty}\frac{M_{n,m}(x_{1},\ldots,x_{m})}{\log n}&= \limsup_{k\rightarrow\infty} \max\bigg\{\frac{M_{n_{k},m}(x_{1},\ldots,x_{m})}{\log(n_{k})},\frac{M_{n_{k}+s_{k}-1,m}(x_{1},\ldots,x_{m})}{\log(n_{k}+s_{k}-1)}\bigg\}\\& =\limsup_{k\rightarrow\infty} \max\bigg\{\frac{s_{k-1}-1}{\log(n_{k})},\frac{s_{k}-1}{\log(n_{k}+s_{k}-1)}\bigg\}\\& =\beta. \end{aligned} \end{align*} $$
Hence,
![]() $(x_{1},\ldots ,x_{m})\in E(\alpha ,\beta ).$
$(x_{1},\ldots ,x_{m})\in E(\alpha ,\beta ).$
It remains to prove that the density of
![]() $\mathbb {K}\subset \mathbb {N}$
is zero. For
$\mathbb {K}\subset \mathbb {N}$
is zero. For
![]() $n_{k}\leq n<n_{k+1}$
with some
$n_{k}\leq n<n_{k+1}$
with some
![]() $k\geq 1{:}$
$k\geq 1{:}$
-
• if
 $n_{k}\leq n< n_{k}+s_{k},$
then
$n_{k}\leq n< n_{k}+s_{k},$
then
 $\sharp \{i\leq n : i\in \mathbb {K}\}=\sum _{j=1}^{k-1}(m_{j}+\iota _{j})+n-n_{k}+1;$
$\sharp \{i\leq n : i\in \mathbb {K}\}=\sum _{j=1}^{k-1}(m_{j}+\iota _{j})+n-n_{k}+1;$
-
• if
 $n_{k}+ls_{k}\leq n<n_{k}+(l+1)s_{k}$
for some
$n_{k}+ls_{k}\leq n<n_{k}+(l+1)s_{k}$
for some
 $l$
with
$l$
with
 $0< l<\iota _{k},$
then we see that
$0< l<\iota _{k},$
then we see that
 ${\sharp \{i\leq n : i\in \mathbb {K}\}=\sum _{j=1}^{k-1} (s_{j}+\iota _{j})+s_{k}+l};$
${\sharp \{i\leq n : i\in \mathbb {K}\}=\sum _{j=1}^{k-1} (s_{j}+\iota _{j})+s_{k}+l};$
-
• if
 $n_{k}+\iota _{k}s_{k}\leq n<n_{k+1},$
then
$n_{k}+\iota _{k}s_{k}\leq n<n_{k+1},$
then
 $\sharp \{i\leq n : i\in \mathbb {K}\}=\sum _{j=1}^{k}(s_{j}+\iota _{j}).$
$\sharp \{i\leq n : i\in \mathbb {K}\}=\sum _{j=1}^{k}(s_{j}+\iota _{j}).$
Consequently,
 $$ \begin{align*} \begin{aligned} \limsup_{n\rightarrow\infty}\frac{\sharp\{i\leq n : i\in\mathbb{K}\}}{n}&\leq \limsup_{k\rightarrow\infty} \max_{0\leq l<\iota_{k}}\bigg\{\frac{\sum_{j=1}^{k-1}(s_{j}+\iota_{j})+s_{k}+l}{n_{k}+ls_{k}}\bigg\}\\& \leq\limsup_{k\rightarrow\infty}\bigg\{\frac{\sum_{j=1}^{k-1}(s_{j}+\iota_{j})+s_{k}+\iota_{k})}{n_{k}}\bigg\}\\& =0, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \limsup_{n\rightarrow\infty}\frac{\sharp\{i\leq n : i\in\mathbb{K}\}}{n}&\leq \limsup_{k\rightarrow\infty} \max_{0\leq l<\iota_{k}}\bigg\{\frac{\sum_{j=1}^{k-1}(s_{j}+\iota_{j})+s_{k}+l}{n_{k}+ls_{k}}\bigg\}\\& \leq\limsup_{k\rightarrow\infty}\bigg\{\frac{\sum_{j=1}^{k-1}(s_{j}+\iota_{j})+s_{k}+\iota_{k})}{n_{k}}\bigg\}\\& =0, \end{aligned} \end{align*} $$
where the last equality follows by the Stolz–Cesàro theorem and (4.2). By Lemmas 2.4 and 2.5,
 $$ \begin{align*}\dim_{H}E_{\alpha,\beta}\geq\dim_{H}\bigg(\prod\limits_{i=1}^{m}E(\mathbb{K},\{a_{n}^{(i)}\}_{n\geq1})\bigg)\geq\sum_{i=1}^{m}\dim_{H}E(\mathbb{K},\{a_{n}^{(i)}\}_{n\geq1})=m.\end{align*} $$
$$ \begin{align*}\dim_{H}E_{\alpha,\beta}\geq\dim_{H}\bigg(\prod\limits_{i=1}^{m}E(\mathbb{K},\{a_{n}^{(i)}\}_{n\geq1})\bigg)\geq\sum_{i=1}^{m}\dim_{H}E(\mathbb{K},\{a_{n}^{(i)}\}_{n\geq1})=m.\end{align*} $$
Similar arguments apply to the remaining cases. We only give the constructions for the proper sequences
![]() $\{n_k\}_{k\geq 1}$
and
$\{n_k\}_{k\geq 1}$
and
![]() $\{s_k\}_{k\geq 1}.$
$\{s_k\}_{k\geq 1}.$
Case 2:
![]() $0<\alpha =\beta <\infty .$
Take
$0<\alpha =\beta <\infty .$
Take
![]() $n_{k}=2^{k}$
and
$n_{k}=2^{k}$
and
![]() $s_{k}=\lfloor \alpha \log n_{k}\rfloor \text { for } k\geq 1.$
$s_{k}=\lfloor \alpha \log n_{k}\rfloor \text { for } k\geq 1.$
Case 3:
![]() $\alpha =0<\beta <\infty .$
Take
$\alpha =0<\beta <\infty .$
Take
![]() $n_{k}=2^{2^{2^{k}}}$
and
$n_{k}=2^{2^{2^{k}}}$
and
![]() $s_{k}=\lfloor \,\beta \log n_{k}\rfloor \text { for } k\geq 1.$
$s_{k}=\lfloor \,\beta \log n_{k}\rfloor \text { for } k\geq 1.$
Case 4:
![]() $\alpha =0, \beta =\infty .$
Take
$\alpha =0, \beta =\infty .$
Take
![]() $n_{k}=2^{2^{2^{k}}}$
and
$n_{k}=2^{2^{2^{k}}}$
and
![]() $s_{k}=\lfloor k\log n_{k}\rfloor ~\text { for } k\geq 1.$
$s_{k}=\lfloor k\log n_{k}\rfloor ~\text { for } k\geq 1.$
Case 5:
![]() $0<\alpha <\beta =\infty .$
Take
$0<\alpha <\beta =\infty .$
Take
![]() $n_{k}=2^{k!}$
and
$n_{k}=2^{k!}$
and
![]() $s_{k}=\lfloor \alpha k\log n_{k}\rfloor \text { for } k\geq 1.$
$s_{k}=\lfloor \alpha k\log n_{k}\rfloor \text { for } k\geq 1.$
Case 6:
![]() $\alpha =\beta =0.$
Take
$\alpha =\beta =0.$
Take
![]() $n_{k}=2^{k}$
and
$n_{k}=2^{k}$
and
![]() $s_{k}=\lfloor \log \log n_{k}\rfloor \text { for } k\geq 1.$
$s_{k}=\lfloor \log \log n_{k}\rfloor \text { for } k\geq 1.$
Case 7:
![]() $\alpha =\beta =\infty .$
Take
$\alpha =\beta =\infty .$
Take
![]() $n_{k}=2^{k}$
and
$n_{k}=2^{k}$
and
![]() $s_{k}=\lfloor k\log n_{k}\rfloor \text { for } k\geq 1.$
$s_{k}=\lfloor k\log n_{k}\rfloor \text { for } k\geq 1.$