No CrossRef data available.
Article contents
ON THE REAL-VALUED GENERAL SOLUTIONS OF THE D’ALEMBERT EQUATION WITH INVOLUTION
Published online by Cambridge University Press: 23 November 2016
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We find all real-valued general solutions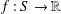 
$f:S\rightarrow \mathbb{R}$ of the d’Alembert functional equation with involution for all 
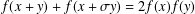$$\begin{eqnarray}\displaystyle f(x+y)+f(x+\unicode[STIX]{x1D70E}y)=2f(x)f(y) & & \displaystyle \nonumber\end{eqnarray}$$
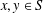$x,y\in S$, where 
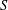$S$ is a commutative semigroup and 
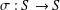$\unicode[STIX]{x1D70E}~:~S\rightarrow S$ is an involution. Also, we find the Lebesgue measurable solutions 
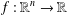$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ of the above functional equation, where 
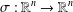$\unicode[STIX]{x1D70E}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ is a Lebesgue measurable involution. As a direct consequence, we obtain the Lebesgue measurable solutions 
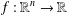$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ of the classical d’Alembert functional equation for all 
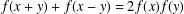$$\begin{eqnarray}\displaystyle f(x+y)+f(x-y)=2f(x)f(y) & & \displaystyle \nonumber\end{eqnarray}$$
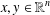$x,y\in \mathbb{R}^{n}$. We also exhibit the locally bounded solutions 
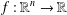$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ of the above equations.
Keywords
MSC classification
Primary:
39B22: Equations for real functions
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (no. 2015R1D1A3A01019573). The third author was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (no. NRF-2015R1D1A1A01059561).
References
Aczél, J. and Dhombres, J., Functional Equations in Several Variables (Cambridge University Press, New York–Sydney, 1989).CrossRefGoogle Scholar
Baker, J. A., ‘The stability of the cosine equation’, Proc. Amer. Math. Soc.
80 (1980), 411–416.Google Scholar
Cauchy, A. L., Cours d’analyse de l’ecole royale polytechnique, Vol. 1. Analyse algebrique, V (Paris, 1821).Google Scholar
Chung, J., ‘Distributional method for the d’Alembert equation’, Arch. Math.
85 (2005), 156–160.CrossRefGoogle Scholar
Chung, J., ‘Distributional solutions of Wilson’s functional equations with involution and their Erdös’ problem’, Bull. Korean Math. Soc.
53 (2016), 1157–1169.CrossRefGoogle Scholar
d’Alembert, J., ‘Addition au mémoire sur la courbe que forme une corde tendue mise en vibration’, Hist. Acad. Berlin
6 (1750), 355–360.Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis (Springer, New York, 2011).CrossRefGoogle Scholar
Sahoo, P. K. and Kannappan, Pl., Introduction to Functional Equations (CRC Press, Boca Raton, FL, 2011).CrossRefGoogle Scholar
Sinopoulos, P., ‘Functional equations on semigroups’, Aequationes Math.
59 (2000), 255–261.Google Scholar
You have
Access