No CrossRef data available.
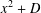 $x^{2}+D$
$x^{2}+D$Published online by Cambridge University Press: 27 May 2019
Let 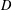 $D$ be a positive nonsquare integer,
$D$ be a positive nonsquare integer, 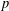 $p$ a prime number with
$p$ a prime number with 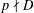 $p\nmid D$ and
$p\nmid D$ and 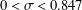 $0<\unicode[STIX]{x1D70E}<0.847$. We show that there exist effectively computable constants
$0<\unicode[STIX]{x1D70E}<0.847$. We show that there exist effectively computable constants 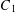 $C_{1}$ and
$C_{1}$ and 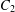 $C_{2}$ such that if there is a solution to
$C_{2}$ such that if there is a solution to 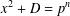 $x^{2}+D=p^{n}$ with
$x^{2}+D=p^{n}$ with 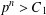 $p^{n}>C_{1}$, then for every
$p^{n}>C_{1}$, then for every 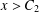 $x>C_{2}$ with
$x>C_{2}$ with  $x^{2}+D=p^{n}m$ we have
$x^{2}+D=p^{n}m$ we have  $m>x^{\unicode[STIX]{x1D70E}}$. As an application, we show that for
$m>x^{\unicode[STIX]{x1D70E}}$. As an application, we show that for 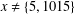 $x\neq \{5,1015\}$, if the equation
$x\neq \{5,1015\}$, if the equation 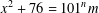 $x^{2}+76=101^{n}m$ holds, then
$x^{2}+76=101^{n}m$ holds, then  $m>x^{0.14}$.
$m>x^{0.14}$.
This research was in part supported by a grant from IPM (No. 95110044).