Let 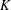$K$ be a field that admits a cyclic Galois extension of degree 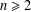$n\geq 2$. The symmetric group 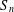$S_{n}$ acts on 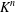$K^{n}$ by permutation of coordinates. Given a subgroup 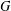$G$ of 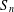$S_{n}$ and 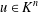$u\in K^{n}$, let 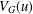$V_{G}(u)$ be the 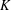$K$-vector space spanned by the orbit of $u$ under the action of $G$. In this paper we show that, for a special family of groups $G$ of affine type, the dimension of 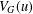$V_{G}(u)$ can be computed via the greatest common divisor of certain polynomials in $K[x]$. 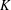We present some applications of our results to the cases $K=\mathbb{Q}$ and $K$ finite.